













Аналоги скоростей центров масс звеньев 2 и 3 получаем в проекциях на оси координат, дифференцируя по обобщенной координате (3.17) и (3.18):
![]() S2x’=
S2x’=![]()
(3.25)
S2y’=![]()
S4x’=![]()
(3.26)
S4y’=![]()
S2x’=-0,03484 S4x’=-0.10277
S2y’=-0,04632 S4y’=-0.012094
Аналитическое определение аналогов ускорений основано на дифференцировании по обобщенной координате уравнений (3.19) и (3.20):
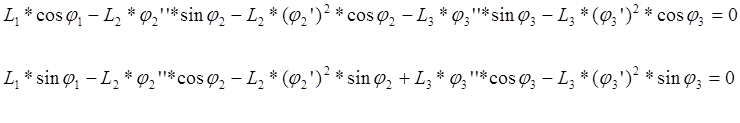
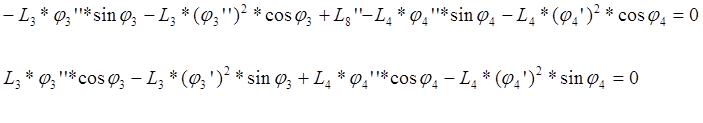
В этих уравнениях j2’’ ,j3’’-аналоги угловых ускорений звеньев 2 и 3.
Для определения j2’’ ,j3’’ решаем систему (3.27) обычным методом или вычитаем в первом уравнении системы угол j3 из аргументов всех тригонометрических функций:
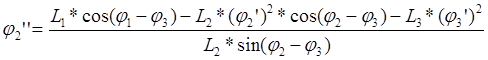 (3.29)
(3.29)
![]()
Из второго уравнения определяем
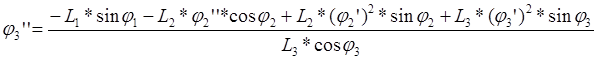
![]()
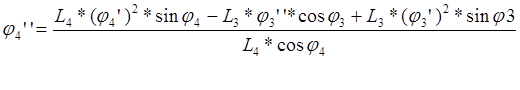 (3.31)
(3.31)
![]()
Из уравнений (3.20) находим L8’’:
![]() (3.32)
(3.32)
![]()
Дифференцируя по обобщенной координате уравнения (3.25) и (3.26), определяем аналоги ускорений центров масс звеньев 2 и 3 в проекциях на оси координат:
![]()
![]()
(3.33)
![]()
![]()
![]()
![]()
![]() -0.15563
-0.15563 ![]() 0.21382
0.21382
![]() -0.02448
-0.02448 ![]() 0.00432
0.00432
2.4 Построение планов скоростей и ускорений
2.4.1 Определение аналогов скоростей исследуемого механизма графическим методом
Решение этой задачи графическим методом основано на построении плана скоростей для третьего положения механизма при j1=19,99°. Так как аналоги скоростей и ускорений не зависят от закона изменения обобщенной координаты, принимаем ω1= 1 рад/с.
План скоростей механизма строим в следующем порядке:
1) находим скорость точки А:
2) из полюса плана скоростей p3 откладываем отрезок, равный 50 мм, изображающий вектор скорости точки А.
3)
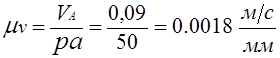 |
4)
|
Уравнение (3.30) решаем графически. Через точку А проводим линию, перпендикулярную АВ, а через полюс P3 – линию, перпендикулярную СВ, до их пересечения в точке c. Векторы pс и bc изображают искомые скорости VB и VBA.
5)
|
Уравнение (3.31) решаем графически. Через точку В проводим линию, перпендикулярную ВD, а через полюс P1 – линию, параллельную СD, до их пересечения в точке d. Векторы pd и bd изображают искомые скорости VD и VDB.
6) из плана скоростей находим:
![]()
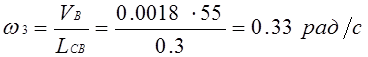 |
|||
|
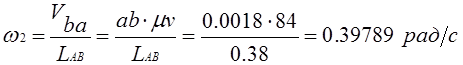 |
|||
|
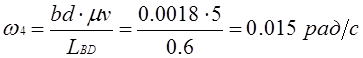 |
|
 |
|
Величина |
φ¢2 |
φ¢3 |
φ¢4 |
L¢5 |
S¢2x,м |
S¢2y,м |
S¢4x,м |
S¢4y,м |
|
Аналити- чески |
0.39974 |
0.33593 |
-0.0155 |
-0.10509 |
-0,0348 |
-0.0463 |
-0.1027 |
-0.01209 |
|
Из плана скоростей |
0.39789 |
0.33 |
0.015 |
0.1008 |
0.0342 |
0.0468 |
0.099 |
0.0117 |
|
Δ,% |
0.46 |
1.76 |
3.2 |
4.08 |
1.72 |
2.5 |
1.07 |
3.2 |
2.4.1 Определение аналогов ускорений исследуемого механизма графическим методом
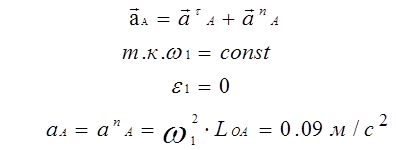 |
План ускорений механизма строим в следующем порядке:
1) находим ускорение точки А:
2) из полюса плана скоростей π3 откладываем отрезок πa=50 мм, изображающий вектор ускорения точки А;
3)
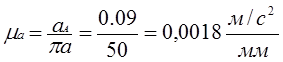 |
4)
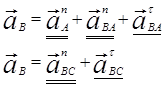 |
|
Нормальные ускорения вычисляем по формулам:
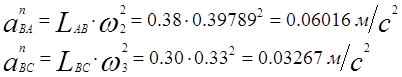 |
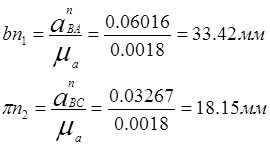 |
Вектор направлен вдоль линии АВ от точки В к точке А – центру относительного вращения звена, а вектор – по линии ВС к центру С.
Через точки n1 и n2 (на чертеже они отмечены как точки) и плана
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.