Динамический синтез рычажного механизма

3.  Динамический синтез рычажного механизма.

   Внутри цикла установившегося движения угловая скорость начального звена машины  периодически  изменяется  из-за постоянного изменения нагрузок, что приводит к нежелательной  неравномерности движения. Неравномерность  движения начального звена характеризуется коэффициентом  неравномерности  движения d, который не должен превышать допустимого значения   [d] . Для снижения  колебаний  угловой скорости  начального  звена  до допустимых пределов в машине предусматривают маховик , который с целью уменьшения  его размеров  устанавливают на быстроходном валу.

При определении момента инерции маховика вместо реального механизма рассматривают его одномастную динамическую модель . Динамическая модель  механизма состоит из одного звена , к которому приложены  движущие силы  Мпд, а также приведены все  силы Мпс, действующие  на звенья машины и моменты инерции звеньев I_M.

3.1 Нахождение приведенного момента инерции и его производной.

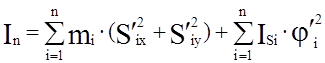где n – число подвижных звеньев, массы и моменты инерции которых заданы, m_i – масса i-го звена; I_Si – момент инерции i-го звена относительно оси, проходящей через центр масс; S¢_ix , S¢_iy – проекции на оси координат аналога скорости центра масс i–го звена;     φ¢_i – аналог угловой скорости i–го звена.

Для данного механизма имеются следующие данные:

m₂=14 кг                        I_s2=0.4 кг*м²

m₃= 20 кг                      I_s3=1.0 кг*м²

m₅ =22 кг                        I_d=0.03 кг*м²

 w_d=260 рад/c

Для рассматриваемого механизма уравнение (3.1) принимает вид:

где

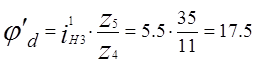Дифференцируя по обобщенной координате j₁ выражение (3.2), находим

производную приведенного момента инерции

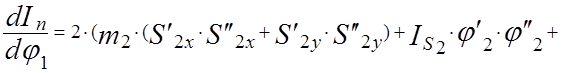Подставив в (3.2) и (3.3) конкретные данные для механизма, находящегося во втором положении, найдем что

Считаем значения In и dIn/dj₁ для остальных положений механизма. Полученные данные заносим в таблицу  и по ним строим графики функции In=f(j₁) и      dIn/dj₁= f(j₁).

3.2 Нахождение приведенного момента сил сопротивления.

 Приведенный момент сил сопротивления определяется по формуле, которая имеет следующий вид:

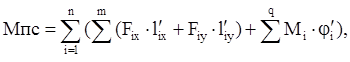где n – общее число подвижных звеньев; m – число внешних сил F, действующих на i-е звено; F_ix, F_iy – проекции силы на соответствующие оси; l’_ix, l’_iy – проекции на соответствующие оси координат аналога скорости точки приложения силы; q – число моментов М, действующих на i-е звено.

 Здесь F_2y, F_y – проекции на ось Y сил веса звеньев 2 и 3, которые соответственно равны:

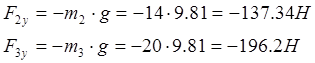  Находим значение Мпс в третьем положении механизма

 Значения Мпс в остальных положениях механизма приведены в таблице .

3.3 Определение приращения кинетической энергии механизма.

  Построив динамическую модель исследуемого механизма, приступим к ее анализу. Анализ динамической модели будем проводить с помощью графоаналитического метода Виттенбауэра. Для построения диаграммы Виттенбауэра необходимо знать законы изменения приведенного момента инерции Iп, который найден выше, и приращения кинетической энергии DТ. найдем закон изменения приращения кинетической       энергии DТ .

   Сначала в соответствие с (4.5) и табл.12 строим график функции Мпс=f(j₁) При построении графика координатную систему располагаем в начале рабочего хода исследуемого механизма . Затем находим работу Ас приведенного момента сил сопротивления Мпс. Работу Ас определяем численным интегрированием функции Мпс=f(j₁). Численное интегрирование проводим, используя метод трапеций, в соответствие с которым

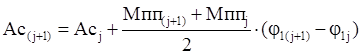Здесь j=1,2,… номер положения механизма, для которог вычисляется работа