Статистическое моделирование. Особенности планирования и проведения исследования по оптимизации процесса

2. Статистическое моделирование

2.1. Основные положения

Разнообразные исследовательские задачи, возникающие как при выявлении физико-типических явлений в изучаемом процессе, так и при решении инженерных проблем, при постановке эксперимента, сводятся к задаче получения статистической модели, которая представляет собой математическую зависимость между выходным и входными параметрами изучаемого процесса или объекта.

Теоретической основой решения задачи статистического моделирования является следующее положение. Предполагается,- что механизм явлений и процессов, протекающих в объекте, можно описать системой дифференциальных уравнений, но из-за слабой изученности и сложности объекта это осуществить невозможно. Система дифференциальных уравнений имеет решение, которое можно разложить в ряд Тейлора по переменный параметрам. Разложение представляет собой степенной полином, коэффициенты которого являются коэффициентами ряда Тейлора, т.е. значениями частных производных в точке, вокруг которой разлагается неизвестная функция, являющаяся решением неизвестных дифференциальных уравнений. Таким образом, поиск связи между выходным и входными параметрами исследуемого объекта, которую называют уравнением регрессии, следует осуществлять в виде степенного многочлена. Наиболее часто используется многочлен первой степени, являющийся самой простой формой статистической модели объекта:

                                             (2.1)

где y  - выходной параметр объекта; x₁…x_m - входные параметры; b₀…b_m - коэффициенты многочлена, определяемые на основе экспериментальных данных статистическим анализом.

Точность статистической модели повышается при переходе к многочленам более высокой степени, что позволяет учитывать большое количество членов разложения Тейлора.

Обработка экспериментальных данных сводится к отысканию коэффициентов многочлена. Значения выходного у   и входных x_i параметров объекта известны из опытных данных, поэтому много­член содержит m+1   неизвестных коэффициентов b₀…b_m. Для их нахождения необходимо иметь m+1    уравнений вида (2.1) и нужно проделать не менее m+ 1 опытов,   чтобы     в каждом из них значения входных параметров x_i составляли свою, отличную от других опытов комбинацию, т.е. опытные, данные позволяли бы решить полученную систему уравнений. При произвольном выборе значений входных параметров x_i для нахождения коэффициентов  b_i регрессии необходимо решить систему m + 1 линейных алгебраических уравнений, что при большом числе m входных параметров является сложной задачей. Уменьшить общий объем вычислений и упростить сам эксперимент можно, варьируя каждый входной параметру, только на двух уровнях. Обозначим эти уровни знаками “-1” (нижний) и ”+1” (верхний) и предположим, что исследуется связь выходного параметра у  о тремя входными параметрами x₁, x₂, x₃. В этом случае для нахождения коэффициентов регрессии необходимо провести четыре опыта по плану, называемому матрицей планирования (табл. 2.1).

Таблица 2.1

В соответствии с матрицей планирования эксперименты выполняют следующий образом: в первом опыте параметры  x₁ и x₂. устанавливают на нижнем уровне, а параметр  x₃ - на верхнем; во втором опыте параметры x₂ и x₃ устанавливают на нижнем уровне, а x₁ - на верхней и т.д. Геометрически такой план эксперимента задается координатами трех равноудаленных друг от друга вершин куба (рис. 2.1), образованного уровнями входных параметров, или, как их принято называть, координатами вершин правильных симплексов. Данный план является насыщенным, поскольку все степени свободы используются для оценки коэффициентов регрессии. Коэффициенты регрессии при использовании подобных планов эксперимента могут быть рассчитаны по следующей формуле:

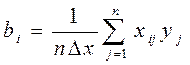                                                    (2.2)

где i, - номер входного параметра и соответствующего ему коэффициента регрессии; j - номер опыта;   n - число опытов;

x_ij-     уровень параметра x_i  в j-м опыте (“-I ” и “+I ”)

-   отклонение параметра x_i  от исходного значения.

Рис. 2.1 Выбор уровней параметров x₁, x₂, x₃ при проведении опытов для определения коэффициентов линейной  регрессии.

Коэффициент b₀ в формуле (2.1) определяется среднеарифметическим значением выходного параметра всех опытов, коэффициентами и исходным значением параметров:

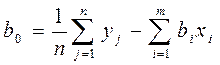                                    (2.3)

Если стоит задача выявления возможного взаимодействия входных параметров, то т уравнение регрессии входят слагаемые, содержащие произведения взаимодействующих параметров, например,