Машиностроение \ Моделирование и оптимизация материалов и технологических процессов

Статистическое моделирование. Особенности планирования и проведения исследования по оптимизации процесса, страница 2

y=b0+b1x1+b2x2+b3x3x2                                      (2.4)

Очевидно, что после введения фиктивного параметра x3=x1x2 исследование сводитcя к рассмотренному случаю (2.1). Для учета всех возможных взаимодействий между входными параметрами необходимо осуществить полный факторный эксперимент, пример плана, которого для случая трех входных параметров приведен в табл. 2.2.

Таблица 2.2

Номер опыта

x1

X2

x3

x1x2

x1x3

x2x3

x1x2x3

y

1

+I

+I

+I

+I

+I

+I

+I

y1

2

-I

+I

+I

-I

-I

+I

-I

y2

3

+I

-I

+I

-I

+I

-I

-I

y3

4

-I

-I

+I

+I

-I

-I

+I

y4

5

+I

+I

-I

+I

-I

-I

-I

y5

6

-I

+I

-I

-I

+I

-I

+I

y6

7

+I

-I

-I

-I

-I

+I

+I

y7

8

-I

-I

-I

+I

+I

+I

-I

y8

Все коэффициенты регрессии имеют одинаковую точность и оцениваются дисперсией выходного параметра

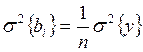                                               (2.5)

Для оценки точности дисперсии воспроизведения выходного параметра проводят дополнительные опыты при постоянном значении входных параметров.

Проверку значимости каждого коэффициента уравнения регрессии осуществляют путем построения доверительного интервала. Коэффициент значим, если произведение его абсолютного значения на шаг варьирования входного параметра больше доверительного интервала входного параметра:

>                                                      (2.6)

Слагаемые уравнения регрессии с незначимыми коэффициентами следует исключить из уравнения (2.6).

При построении статистической модели исследуемого объекта первоначально используют простейшую линейную форму уравнения регрессии, которая не всегда соответствует истинной взаимосвязи между выходным и входными параметрами объекте. Соответствие формы уравнения регрессии исследуемому объекту проверяют по дисперсии адекватности

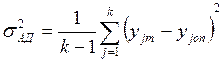                                              (2.7)

где yjm и yjon- значения выходного параметра, рассчитанные по статистической модели и полученные при дополнительных опытах; к- число дополнительных опытов, проведенных с целью проверки соответствия формы уравнения регрессии исследуемому объекту.

Опыты по определению дисперсии адекватности следует проводить при различных значениях входных параметров.

Для проверки адекватности модели удобен известный в статистике F-критерий Фишера;

                                                  (2.8)

Значение F, рассчитанное по формуле (2.8), сравнивают с табличным значением, зависящим, от числа опытов при определении дисперсии адекватности и доверительной вероятности. Если вычисленное значение F-критерия не превышает табличного, то с доверительной вероятностью модель можно считать адекватной, т.е. соответствующей истинной взаимосвязи параметров объекта. При превышении табличного значенияследует перейти к модели в виде полинома более высокой  степени - уравнению регрессии второго порядка.

2.2. Особенности планирования и проведения исследования по оптимизации процесса

Скачать файл