Статистическое моделирование. Особенности планирования и проведения исследования по оптимизации процесса, страница 3

Задачей исследования с целью оптимизации процесса является определение таких значений входных параметров, при которых выходной параметр процесса имеет максимальное или минимальное значение. С целью уменьшения количества опытов исследование осуществляют в определенной последовательности,

В области первоначального значения входных параметров проводят серию опытов, необходимую для получения линейного уравнения регрессии. После нахождения адекватного линейного уравнения регрессии изменяют входные параметры в направлении градиента этого уравнения в области оптимума, т.е. пропорционально соответствующим коэффициентам уравнения. Выбирая произвольно для одного из параметров шаг движения по градиенту, вычисляют шаги для остальных входных параметров:

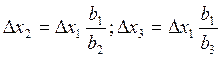                                            (2.9)

Затем последовательно к исходному значению параметров прибавляют или вычитают из него (в зависимости от знака коэффициента регрессии и направления движения) рассчитанные шаги и при полученном таким образом значении входных параметров ставят опыты. Опыты прекращают, когда достигается область оптимума (рис. 2.2)

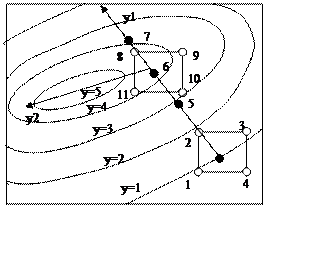
Рис. 2.2 Последовательность проведения опытов по поиску максимума выходного параметра

Первоначально выполняются опыты в точках 1-4 и определяется направление y₁ , в котором необходимо изменять входные параметры x₁ и x₂ для последовательного проведения опытов 5,6,7, прекращаемые после достижения максимального значения выходной величины, В этой  области выполняются опыты в точках 8-11 по определению нового направления у₂ . Еcли какие-то ограничения не позволяют          изменять некоторые параметры, то их фиксируют на достигнутом уровне,  продолжая изменение других параметров.

После достижения области оптимума либо удовлетворяются результатом, либо ставят дополнительный эксперимент с целью получения статистической модели для последующей белее точной оптимизации процесса.

2.3. Пример статистического моделирования процесса

Задача. Математически описать зависимость между параметрами режима точечной контактной сварки. Целью исследования является получение расчетной формулы, связывающей значение и длительность импульса сварочного тока, усилие сжатия электродов и толщину свариваемых точечной контактной сваркой листов из малоуглеродистой стали, обеспечивающих стандартные размеры литого ядра.

1. Теоретический анализ задачи. Целью анализа является выявление приблизительного вида искомой взаимосвязи для упрощения экспериментального исследования. Рассмотрим соотношения между отдельными параметрами сварочного процесса.

Стандартные размеры литого ядра определяются толщиной свариваемых листов. При приблизительно одинаковой их толщине нормальными считаются: проплавление деталей, генное 2/3 их толщины, и диаметр литого ядра d_я равный, где - толщина листа. Объем V и теплоемкость C_v зоны тепловыделения при точечной контактной сварке нарастают пропорционально квадрату толщины листов:

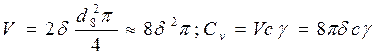
где - удельная теплоемкость металла.

Размеры литого ядра   определяются температурой в зоне тепловыделения в момент выключения тока, которая пропорциональ­на теплоcодержанию металла этой зоны. Теплосодержание Q ме­талла между электродами машины в процессе сварки изменяется по экспоненциальному закону:

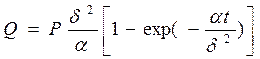
где P  -мощность; α-       температуропроводность        металла. Мощность, выделяемая током I в деталях, зависит от сопротивления R, на величину которого оказывает влияние усилие F снятия электродов:

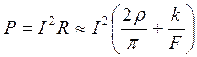
где ρ - удельное электросопротивление металла деталей;

К - коэффициент, зависящий от состояния поверхности деталей.

Для получения литого ядра нормальных размеров необходи­мо нагреть металл в зоне сварки до некоторой средней темпера­туры  T₀=Q/C_v Для этого необходимо, чтобы через детали про­текал ток I   в течение времени t;