Величина обменного взаимодействия зависит от расстояния между атомами в кристаллических решетках. На рис. 5.4 приведена схематическая зависимость обменного интеграла (A) от отношения межатомного расстояния (d) к радиусу (a) незавершенной внутренней оболочки.
Как видно из рис.5.4 при значительных расстояниях обменный интеграл равен нулю. При сближении атомов за счет появления обменной энергии обменный интеграл растет в положительном направлении. Однако, на расстояниях превышающих межатомное, обменные силы ничтожно малы и
Рис. 5.4. Схематическая зависимость обменного интеграла (А)
от отношения (d/a) (кривая Бете-Слетера)
не могут противостоять тепловому разупорядочиванию спинов, магнитные моменты атомов в этом случае будут располагаться хаотично, и материал будет обладать парамагнитными свойствами. Сближение атомов приводит к возрастанию обменных сил, и спиновые моменты электронов соседних атомов начинают располагаться параллельно друг другу, вследствие чего возникает ферромагнитное состояние. С уменьшением межатомного расстояния спиновые магнитные моменты удерживаются в параллельном положении все более прочно, а величина обменного интеграла возрастает и достигает максимума. Затем величина обменного интеграла уменьшается , обращается в ноль и становится отрицательной. При этом спины устанавливаются антипараллельно. Состояние вещества, характеризуемое самопроизвольной антипараллельной ориентацией спинов, называется антиферромагнетизмом.
Таким образом, для возникновения ферромагнитного состояния необходимо наличие некоторого интервала расстояний между соседними атомами, при котором обменный интеграл имеет положительное значение. Это второе условие существования ферромагнетизма.
Значение обменного интеграла приближенно можно определить из выражения
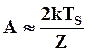(5.30)
где Тs - температура точки Кюри; Z – координационное число.
Из (5.30) видно, что значение обменного интеграла зависит от температуры Кюри: чем больше обменный интеграл, тем необходима большая тепловая энергия для разрушения ферромагнитного состояния
 |
5.7. Влияние температуры на самопроизвольную
намагниченность ферромагнетиков
На состояние самопроизвольной намагниченности большое влияние оказывает тепловое поле. В соответствии с теорией Вейсса величина общего магнитного поля ферромагнетика складывается из внешнего поля Н и поля Вейсса Нi. Если внешнее поле отсутствует и нет теплового разупорядочивания (Т = 0), то ферромагнетик будет намагничен до насыщения, а параллельная ориентация спиновых магнитных моментов будет удерживаться внутренним полем Нi. Тогда суммарный магнитный момент насыщения при Т = 0 составит
(5.31)
где Ms – магнитный момент, соответствующий намагниченности насыщения; N0 – число носителей магнетизма; μВ – магнетон Бора.
При нагревании ферромагнетика вследствие дезориентирующего действия теплового поля и повышения кинетической энергии электронов возможно самопроизвольное переворачивание их спинов. В результате переворачивания спиновых моментов антипараллельно их общей ориентации намагниченность тела будет уменьшаться. В области низких температур эта убыль почти незначительна, а с повышением температуры намагниченность падает все быстрее. В области высоких температур этот спад идет стремительно, и при некоторой температуре (температура Кюри) ферромагнетизм исчезает. Самопроизвольная намагниченность становится нулевой, и ферромагнетик переходит в парамагнитное состояние (рис. 3.5).
Рис.5.5. Влияние температуры на ферромагнитное состояние материала
Процесс спиновых разворотов можно с некоторым приближением рассматривать как тепловое движение частиц. Если принять это допущение, то, зная количество перевернутых спинов в какой-либо момент времени, можно определить величину уменьшения магнитного момента за счет теплового возбуждения. Согласно статистике Больцмана, количество перевернутых спинов можно найти из выражения
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.