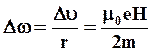Магнитные свойства материалов. Носители магнетизма. Диамагнетизм электронного газа. Намагничивание ферромагнетиков. Магнитные свойства гетерогенных сплавов, страница 3

                                                                          (5.20)

Подставив полученное выражение в (5.12) можно определить изменение магнитного момента орбитального движения электрона за счет наложения внешнего поля

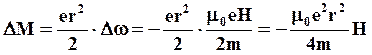                                 (5.21)

Знак минус указывает, что индуцированный магнитный момент направлен против вектора напряженности внешнего наложенного поля.

Для определения изменения магнитного момента атома необходимо просуммировать значение ΔМ по всем электронам. Тогда суммарный диамагнитный момент атома составит

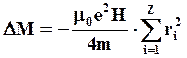                                                                       (5.22)

где Z – число электронов в атоме; r_i – радиус орбиты каждого их Z электронов.

Так как все ориентации орбит равновероятны, то  среднее значение радиуса определяется выражением

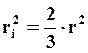                                                                                                   (5.23)

где r – радиус орбиты

Тогда (5.22) примет вид

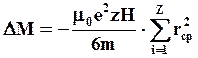                                                                                 (5.24)

где r_ср – средний радиус орбиты.

Если выражение (5.24) умножить на число Авогадро N получим молярную намагниченность, из которой можно определить молярную диамагнитную восприимчивость

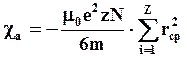                                                                        (5.25)

При выводе соотношения (5.25) было принято, что поле Н перпендикулярно к плоскости орбиты электрона. В общем случае орбита наклонена к вектору напряженности поля, поэтому под действием поля вызывается прецессия орбиты (рис. 5.2). В результате прецессионного движения нормаль р к плоскости орбиты будет описывать конус вокруг вектора напряженности магнитного поля Н с постоянной угловой скоростью Δω.

Рис. 5.2. Прецессия орбиты электрона

Такое движение  орбиты называется ламоровой прецессией. Из теоремы Ламора следует, что движение электрона в атоме под действием магнитного поля  относительно вектора напряженности Н происходит так же, как и в отсутствии поля. При этом имеет место общая прецессия, благодаря которой угловая частота меняется на величину ламоровой частоты  Δω_L = Δω, для которой справедлива формула (5.20).

На рис. 5.3  приведены схемы образования диамагнитного момента при вращении электрона в разных направлениях относительно вектора напряженности магнитного поля. Независимо от направления вектора магнитного момента индуцированный момент будет направлен против поля, т.е. в обоих случаях возникает диамагнитная составляющая.

Если две орбиты, изображенные на рис. 5.3, принадлежат одному атому, то его намагниченность будет равна нулю, а при наложении внешнего магнитного поля появится диамагнитный момент равный  -2ΔМ, так как оба вектора ΔМ имеют одно и то же направление (против поля).

Типичными диамагнетиками являются благородные газы, состоящие из атомов с завершенными электронными оболочками. Магнитные моменты всех электронов скомпенсированы, поэтому благородные газы не имеют собственного магнитного момента. Любой элемент является диамагнитным, если он ионизирован на столько, что  электронная оболочка его атома такая же, как у атома благородного газа.

Рис. 5.3. Схема образования диамагнитного момента

Все неметаллы (за исключением кислорода и графита) являются диамагнетиками. Причем их магнитная восприимчивость близка к восприимчивости инертных газов вследствие того, что электроны в неметаллах не свободны, а их межатомная связь преимущественно ковалентная. При ковалентной  связи  магнитные моменты двух спаренных электронов, связывающих два соседних атома, скомпенсированы, а их суммарный  магнитный момент равен нулю.

Из металлов к диамагнетиками относятся медь, кадмий, бериллий, ртуть, серебро, золото,  висмут, бор, свинец и другие. Диамагнитная восприимчивость, как правило, растет с увеличением номера элемента в Таблице Менделеева.