Магнитные свойства материалов. Носители магнетизма. Диамагнетизм электронного газа. Намагничивание ферромагнетиков. Магнитные свойства гетерогенных сплавов, страница 2

где  e и m – заряд и масса электрона.

Магнетон Бора принимается за атомную единицу магнитного момента.

Из (5.7) и (5.8) следует, что отношение механического и магнитного моментов спина равно

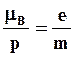                                                                                            (5.9)

При движении  электрона вокруг атома также создается механический момент количества движения и магнитный момент. Момент количества движения определяется выражением

                                                                                          (5.10)

где υ – линейная скорость электрона;  r – радиус обитали.

Орбитальный магнитный момент при этом будет равен

                                                                                                   (5.11)

где ν – частота вращения.

Принимая   и   , где  ω – угловая скорость, получим

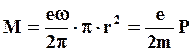                                                                                (5.12)

Тогда

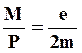                                                                                         (5.13)

Сравнение выражений (5.9) и (5.13) позволяет утверждать, что гиромагнитное отношение спиновых моментов в два раза больше, чем орбитальных. Следовательно, в создании магнитных свойств вещества больший вклад принадлежит спинам магнитных составляющих.

Магнитный момент многоэлектронного атома представляет собой сумму магнитных моментов всех электронов, включая орбитальные и спиновые. Если число электронов в атоме четно, а векторы их магнитных моментов направлены навстречу друг другу, то  магнитный момент атома будет равен нулю. Такой случай имеет место у атомов инертных элементов.

5.3.  Диамагнитные свойства

Диамагнетизм является универсальным свойством, присущий всем телам, но благодаря своей малости он обнаруживается только тогда, когда другие магнитные эффекты отсутствуют или настолько малы, что перекрываются им. Обычно диамагнетизм проявляется в том случае, когда магнитные моменты всех электронных орбит и спинов взаимно скомпенсированы.

Возникновение диамагнетизма обусловлено орбитальным движением электрона, как изолированных атомов, так и атомов, составляющих молекулы и кристаллы. Диамагнетизм возникает при наложении магнитного поля вследствие электромагнитной индукции, приводящей к появлению добавочного магнитного момента, направленного против вектора напряженности внешнего поля. Вследствие появления добавочного магнитного момента диамагнетик, помещенный во внешнее поле, выталкивается из него.

Явление диамагнетизма удобнее рассматривать с позиций классической теории электронного строения материала. Определим величину изменения магнитного момента ΔМ,  для этого рассмотрим электрон, движущийся по замкнутой круговой орбите с угловой скоростью ω.  Будем считать, что радиус круговой орбиты равен радиусу наружной сферы орбитали. При таком движении на него действует центростремительная сила равная

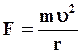                                                                                         (5.14)

Если на этот электрон наложить магнитное поле, вектор напряженности  Н которого перпендикулярен плоскости орбиты, то появится добавочная сила Лоренца, направленная по радиусу и равная

                                                                                              (5.15)

где μ₀ – магнитная постоянная, равная проницаемости вакуума.

Тогда результирующая сила, действующая на электрон, будет равна

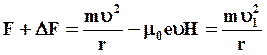                                                                  (5.16)

где υ₁ – результирующая скорость движения электрона.

Из (5.16) следует

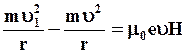                                                                     (5.17)

или                                     

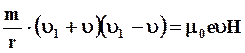                                                                    (5.18)

Если предположить, что изменение скорости при наложении поля незначительно, то можно принять υ₁ +  υ ≈ 2υ, тогда

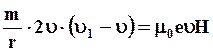
или

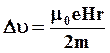                                                                                 (5.19)

Изменение линейной скорости орбитального движения электрона при неизменном радиусе орбиты соответствует изменению угловой скорости