Магнитные свойства материалов. Носители магнетизма. Диамагнетизм электронного газа. Намагничивание ферромагнетиков. Магнитные свойства гетерогенных сплавов, страница 5

Рассмотрим взаимодействие молекул с постоянными магнитными моментами М₀. Максимальная магнитная энергия взаимодействия таких двух элементарных магнетиков даже при очень низких температурах на порядок и более ниже их тепловой энергии.  Следовательно, в отсутствии внешнего магнитного поля тепловое движение нарушает ориентацию магнитных моментов, и результирующая намагниченность парамагнетика равна нулю. При наложении внешнего магнитного поля магнитные моменты элементарных магнетиков начинают ориентироваться параллельно вектору напряженности наложенного поля. Энергия магнитного взаимодействия магнетиков с внешним полем (без учета взаимодействия магнетиков друг с другом) будет зависеть от угла φ между векторами М₀ и напряженностью внешнего магнитного поля Н, при этом сама энергия взаимодействия может быть рассчитана но формуле

                                                                               (5.20)

минимальная энергия магнитного взаимодействия будет иметь место при φ = 0, что соответствует параллельной ориентации магнитных моментов магнетиков относительно вектора напряженности внешнего магнитного поля.

Только при очень высокой напряженности внешнего магнитного поля  или сверх низкой температуре тела магнитные моменты М₀ могут быть строго ориентированы в направлении вектора напряженности Н. Во всех других случаях при любой конечной температуре соударение атомов из-за теплового движения будет приводить к разупорядочению моментов М₀, в результате чего суммарный момент множества парамагнитных частиц будет несколько меньше возможного максимального значения. Величина и степень  ориентации всех моментов М₀ будет зависеть от соотношения магнитной и тепловой энергий.

Вероятность ориентации магнитных моментов под углом φ определяется функцией Больцмана

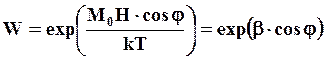                                           (5.21)

где  

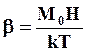
Средний магнитный момент всего тела с учетом распределения Больцмана описывается выражением

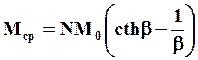                                                                (5.22)

где N – количество магнитных частиц с магнитным моментом М₀.

Если напряженность внешнего магнитного поля слабая, а температура частицы высокая, то β << 1. При малых значениях β

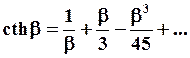                                                                      (5.23)

Ограничившись первыми двумя членами ряда, получим

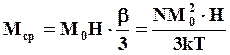                                                                          (5.24)

Так как магнитная восприимчивость есть отношение магнитного момента к напряженности внешнего магнитного, то при равенстве N числу Авогадро N_A получим значение молярной  магнитной восприимчивости парамагнитного вещества

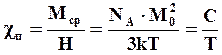                                                                  (5.25)

где 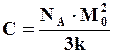   - постоянная Кюри.

Полученное выражение (5.25) представляет закон Кюри, согласно которому магнитная восприимчивость парамагнитно-упорядоченных частиц обратно пропорциональна температуре.

Однако для многих веществ, в частности, твердых парамагнитных металлов, в области низких температур или сильных магнитных полей закон Кюри не выполняется. Действительно, при низкой температуре отношение (Н/Т) стремится к бесконечности, а намагниченность при этом должна  стремиться к насыщению, но эта закономерность не имеет места. П. Вейсс предположил, что при больших значениях напряженности внешнего магнитного поля  оно одновременно вызывает возникновение в частице направленного эффективного внутреннего магнитного поля, пропорционального ее намагниченности I. В результате магнитная восприимчивость парамагнетика будет подчиняться более уточненному закону Кюри-Вейсса

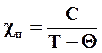                                                                             (5.26)

где Θ – постоянная для данного парамагнетика величина, имеющая размерность температуры и называемая парамагнитной точкой Кюри.

При Т = Θ парамагнитная восприимчивость стремится к бесконечности, это означает появление ферромагнетизма или антиферромагнетизма.