Учебное пособие по курсу «Арифметические и логические основы вычислительной техники»

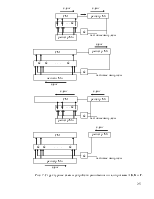
независимость образования разрядов числа, в силу чего каждый разряд несет информацию обо всем исходном числе, а не о промежуточном числе, получившемся в результате формирования младших разрядов (позиционная система счисления). Отсюда вытекает независимость разрядов числа друг от друга и возможность их параллельной обработки, что в свою очередь в дальнейшем позволяет вводить принципиально новые методы арифметического контроля. При введении дополнительного контрольного основания остаток, взятый по этому основанию, при его избыточности позволяет контролировать и исправлять ошибки в цифрах по рабочим основаниям;

§ малоразрядность остатков, представляющих число. Ввиду малого количества кодовых комбинаций открывается возможность построения табличной (не вычислительной) арифметики.

          Недостатки:

§ невозможность визуального сопоставления чисел, так как внешняя запись числа не дает представления о его величине;

§ отсутствие простых признаков выхода результата операций за пределы [0,ρ];

§ ограниченность действий системы сферой целых положительных чисел;

§ получение во всех случаях точного результата исключает возможность приближенных вычислений, округлений.

Представление отрицательных чисел в СОК

          Рассмотрим правила выполнения операций вычитания в системе остаточных классов для чисел А и В, удовлетворяющих условию А-В Í[0,];

          А = (a₁, a₂, ... ,a_n),

          В = (b₁, b₂, ... ,b_n),

          A-B = (g₁, g₂, ... ,g_n),

при этом А<ρ, B< ρ, 0<=А-В< ρ.

          Как и ранее, получаем для А-В

          g_i = a_i - b_i - ,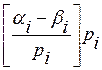

          g_i º a_i - b_i (mod p_i).

 Операция вычитания при положительном результате выполняется вычитанием соответствующих цифр разрядов, в результате приводится наименьший положительный остаток.

          При отрицательной разности цифр берется ее дополнение к основанию. При этом знак результата в результате никак не отражен.

          Возникает необходимость ввести специальным образом знак в представление числа и определить правила выполнения операций, обеспечивающих получения не только величин, но и знака результата.

          Рассмотрим варианты введения отрицательных чисел.

          Пусть p₁, p₂, ... p_n - основания системы счисления.

              = p₁, p₂, ... ,p_n  - диапазон представимых чисел.

          Пусть   p₂ =2. Обозначим через В СОK  Р=(1, 0, 0, ... , 0).

 Будем оперировать числами, лежащими в диапазоне 0≤ |N| <P.

          Примем в качестве нуля число Р и представим положительные числа N= |N|  как N' = P + |N|, отрицательные числа N = - |N| как N' =P - |N|.

 Таким образом, N' =P+N - искусственная форма (общая форма представления + и - чисел).

          Следовательно, мы всегда будем иметь дело с положительными числами, так как |N|<P.

          Но числа в интервале [0,P) в искусственной форме будут отображать отрицательные, а в интервале [P,) - положительные числа.

          Операцию сложения и вычитания можно выполнять следующим образом:

          N′₁ = P + N₁,

          N′₂ = P + N₂,

          N′₁ + N′₂ = P + N₁ + P + N₂ = 2P + (N₁ + N₂).

          Для суммы N₁ + N₂  искусственная форма:

          (N₁ + N₂)′ = P + (N₁ + N₂),

          (N′₁ + N′₂) = N′₁ + N′₂ - P

или так как P = (1, 0, 0, ..., 0), то (N₁ + N₂) ′ =N′₁ + N′₂ + P.             (9)

          Пример.  Пусть p₁ = 2, p₂ = 3, p₃ = 5, p₄ = 7. 

P = 3∙5∙7 = 105

          N₁ = 17, N₂ = 41

          N′₁ = (1, 0, 0, 0) + (1, 2, 2, 3) = (0, 2, 2, 3),

N′₂ = (1, 0, 0, 0) + (1, 2, 1, 6) = (0, 2, 1, 6),

согласно (9)  (N₁ + N₂) ′ =  (0, 2, 2, 3) + (0, 2, 1, 6) + (1, 0, 0, 0) = (1, 1, 3, 2) - искусственная форма N₁ + N₂, что можно проверить, перейдя и десятичной системе счисления.

          (17 + 41)′ = (58)′ = 105 + 58 = (1, 0, 0, 0) + (0, 1, 3, 2) = (1, 1, 3, 2)

          Пример.   N₁ = 17, N₂ = 41.

          N′₁ = (0, 2, 2, 3),

          N′₂ = (1, 0, 0, 0) - (1, 2, 1, 6) = (0, 1, 5, 1),

          (N₁ + N₂)′ = (0, 2, 2, 3) + (0, 1, 5, 1) + (1, 0, 0, 0) = (1, 0, 1, 4),

          (17 - 41)′ = (-24)′ = 105 - 24 = (1, 0, 0, 0) - (0, 0, 4, 3) = (1, 0, 1, 4).

          Переход из положительного числа в отрицательное и обратно, то есть образование его дополнительного кода производится вычитанием данного числа из числа  (1, p₁, p₂, ... ,p_n).

          +41 = (1, 2, 1, 6)

          - 41 = (1, 3, 5, 7) - (1, 2, 1, 6) = (0, 1, 4, 1) = 64.

          Следует отметить, что если вычитаемое уже было представлено в искусственной форме, то для получения дополнительного кода надо его вычитать из (2,p₁,p₂, ..., p_n).

Контроль работы цифрового автомата

          В процессе вычислений происходит постоянная передача и преобразование информации, находящейся в памяти ЭВМ, арифметическом