Санкт-Петербургский Государственный Политехнический Университет
Факультет Технической Кибернетики
Кафедра Системного Анализа и Управления
Задание по вычислительной математике №2
«Решение дифференциальных уравнений»
Вариант №9
Выполнил ст. гр. 2082/2 Серебряков Д.В.
Проверил Куприянов В.Е.
Санкт-Петербург
2006
1. Постановка задачи.
Исследовать зависимость устойчивости и погрешности решения дифференциального уравнения заданным численным методом. Сравнить полученное решение с аналитическим решением и результатом использования стандартного сольвера Matlab. Дифференциальное уравнение имеет вид: a0 y’’’(t) + a1 y’’(t) + a2 y’(t) + y(t) = 10. Начальные условия: y(0) = y’(0) = y’’(0) = 0. Интервал: t Є [0, tm].
Вариант №9.
a0 = 0,12376; a1 = 1,015; a2 = 0,323; tm = 40 [с].
Метод Эйлера-Коши 2 порядка точности.
2. Метод решения.
Метод Эйлера-Коши 2 порядка точности:
xk+1 = xk + h/2(f(tk, xk) + f(tk + h, xk + hf(tk, xk))
3. Аналитическое решение.
0,12376y’’’ + 1,015y’’ + 0,323y’ + y = 10;
Корни характеристического многочлена:
α1 = -8,0014; α1,2 = -0,1 ± 0.9999i;
Соответствующие им частные решения диф. уравнения имеют вид:
y1 = e-8,0014; y2 = e-0,1tcos(0,9999t); y3 = e-0,1tsin(0,9999t);
Общее решение:
y = C1y1 + C2y2 + C3y3 + _y;
Дифференцируя общее решение необходимое число раз и исходя из начальных условий, составляем систему, решая которую, находим:
y = -0,1517 e-8,0014 – 9,3565 e-0,1tcos(0,9999t) – 2,1491 e-0,1tsin(0,9999t) + 9,5082
4. Структура программы
1) function main(n)
Входные значения: n – количество точек разбиения
Функция main вызывает функции MyEK2 и ode45, решая дифф. уравнение, строит графики полученных решений и графики погрешностей.
2) function dydt = de(t, y)
Входные данные: t – значение аргумента;
y – значение вектор функции.
Выходные данные: dydt – значение функции de(t, y)).
3) function [T, y] = MyEK2(t, x0, h, k)
Вх. значения: t – начальное значение по шкале абцисс,
x0 – массив начальных значений,
h – шаг, k - количество точек разбиения
Вых. значения: T – массив точек разбиения,
y – соответсвующее точкам разбиения решение
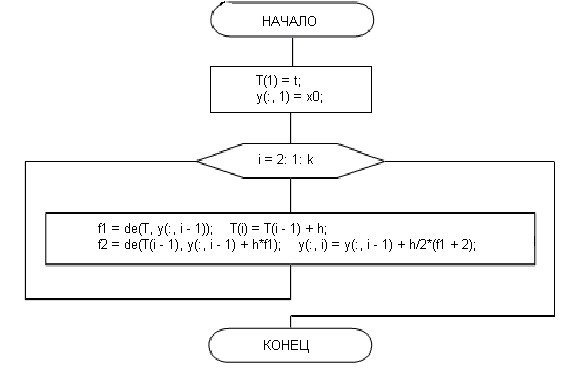
5. Текст программных модулей.
function main(n)
y0 = [0; 0; 0];
t0 = 0;
tm = 40;
h = (tm - t0)/n;
subplot(2,1,1);
for k = 1: n
T(k) = t0 + (k-1)*h;
Y(k) = -0.1517*exp(-0.80014*T(k)) - 9.3565*exp(-0.1*T(k))*cos(0.9999*T(k)) - 2.1491*exp(-0.1*T(k))*sin(0.9999*T(k)) + 10;
end
[t_s, y_s] = ode45(@de, T, y0);
[t, y] = MyEK2(t0, y0, h, n);
plot(t_s, y_s(:,1), ':g', t, y(1, :), '-.r', T, Y, '-b'), grid on;
subplot(2,1,2);
plot(T, Y - y_s(:, 1)', ':r', T, Y - y(1, :), '-.b'), grid on;
function dydt = de(t, y)
a(1) = 0.12376;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.