Решение дифференциальных уравнений, страница 2

a(2) = 1.015;

a(3) = 0.323;

dydt = [y(2); y(3); 1/a(1)*(10 - a(2)*y(3) - a(3)*y(2) - y(1))];

function [T, y] = MyEK2(t, x0, h, k)

T = zeros(1, k);

T(1) = t;

y = zeros(3, k);

y(:, 1) = x0;

for i = 2: 1: k

    f1 = de(T, y(:, i - 1));

    T(i) = T(i - 1) + h;

    f2 = de(T(i - 1), y(:, i - 1) + h*f1);

    y(:, i) = y(:, i - 1) + h/2*(f1 + f2);

end

6.  Решение.

n = 40;

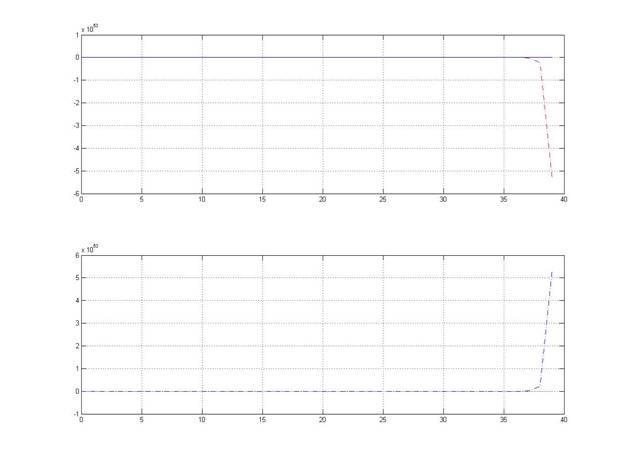
n = 100;

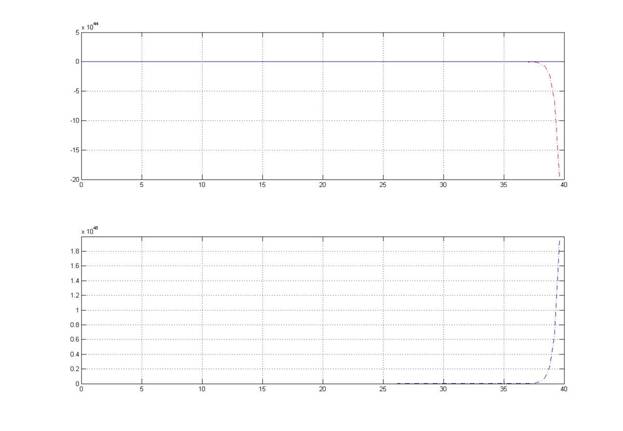
n = 400;

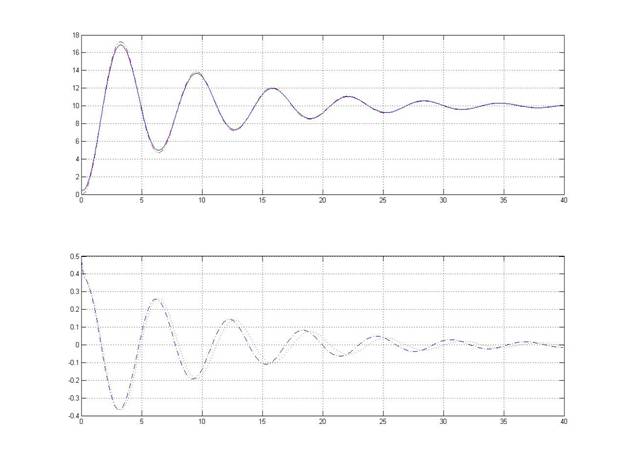
7.  Выводы.

   Были построены графики решения уравнения и графики погрешностей при  n = 40, 100, 400. С увеличением количества шагов вдвое, а значит, уменьшением величины шага, амплитуда колебаний увеличивается, причем она также увеличивается со временем. При  n = 400 погрешность заметно меньше.