|
Формирование линейного и кубического сплайн-интерполяторов. Оценка возможности и точности интерполяции.
Ключевые термины раздела 10.
интерполяция данных – построение функциональной или расчетной зависимости по точкам (строительным) данных, восполняющей отсутствующие данные в промежутках между этими точками.
сплайн – интерполяционнаякривая, аппроксимирующая график функции кусками полинома определенной степени на цепочке интерполяционных (строительных) точек, в которых сплайн и ряд его производных равны аппроксимируемой функции и её соответствующим производным. По степени применяемого полинома сплайн называется линейным, параболическим, кубическим и т.д.
L-сплайн, р-сплайн, с-сплайн – кубические сплайны Mathcad, векторы вторых производных которых в наборе интерполяционных точек (vx, vy) формируются функциями соответственно lspline(vx,vy), pspline(vx,vy), cspline(vx,vy).
Под интерполяцией подразумевается создание по ранее полученным расчетным или экспериментальным данным (строительным или опорным точкам) – значениям аргумента х и функции у неизвестного вида (например, границы устойчивости на рис. 7.8) – некоторой формулы, позволяющей рассчитывать значения функции у при промежуточных между опорными значениях аргумента х.
Интерполяция в Mathcad может быть реализована на основе В-сплайна, кубических сплайнов и кусочно линейной кривой. Рассмотрим последние два вида интерполяции, в которых используется семь функций:vsL:=lspline(vx,vy), vsp:=pspline(vx,vy), vsc:=cspline(vx,vy), iLs(x):=interp(vsL,vx,vy,x), ips(x):=interp(vsp,vx,vy,x), ics(x):=interp(vsc,vx,vy,x) и iL(x):=linterp(vx,vy,x). Первые три предназначены для создания вектора vs вторых производных в опорных точках, представляемых векторами координат vxиvy, для последующего использования соответственно в L-, p- и c-сплайн-интерполяторах (четвертая, пятая и шестая функции).iLs(x) – это линейный интерполятор, соединяющий опорные точки отрезками прямых.
Построение кривой на примере интерполяции границы области устойчивости на рис. 7.8 разд. 7 – на рис. 10.1:
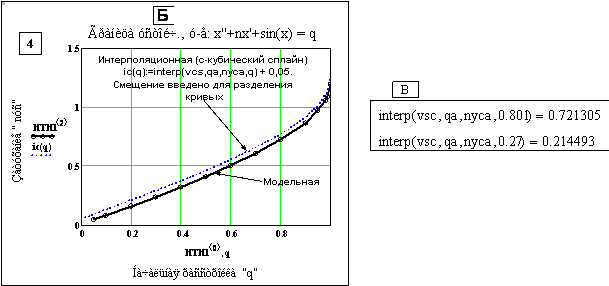
А – этапы построения; Б – сравнение исходной границы и интерполяционной (в пределах трех знаков после запятой расхождения кривых не наблюдается); В – вычисление конкретных значений затухания в промежуточных точках с использованием интерполяционной формулы nус(q промеж.), равнойinterp(vs,q,nус,q промеж.).
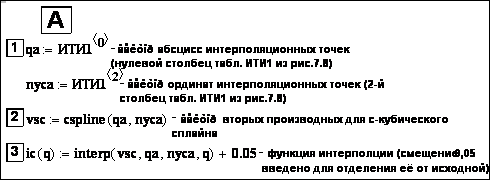 |
Рис. 10.1. Этапы построения интерполяционной кривой (А), ее использование для построения границы (Б) и для вычисления в отдельных промежуточных между опорными точках (при q = 0,801 и 0,27), (В). На графике для ic(q) шаг по q равен 0, 001 – выбран пакетом Mathcad
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.