Сплайн-интерполирование расчетных и экспериментальных данных (Глава 10 Методики применения пакета Mathcad для решения научных и типовых общетехнических задач), страница 2

Продолжение рис. 10.1

Этапы построения интерполяционной кривой                                                                      (на примере рис. 10.1)

  1.   Создайте векторы: абсцисс аппроксимации  vxа (в рассматриваемом примере – q_а) и ординат  vyа = nус(q_а), используя измерительную панельку Trace,в характерных точках интерполируемой кривой: начальной и конечной, в точках максимума и минимума, перегиба, пересечения оси абсцисс, изменения наклона, конечного скачка и т.п..

  2.  Введите вектор сплайна vs (vsL или  vsр или  vsс, являющегося вектором вторых производных соответственно для линейного, параболического и кубического сплайнов) через присвоение одному из трех видов функций (lspline(vxа,vyа), pspline(vxа,vyа), cspline(vxа,vyа), которые формируют векторы вторых производных): в примере - cspline(q_а, nус_а).

  3.  Введите аппроксимирующую функцию iс(q_а) через присвоение ее функции интерполяцииinterp(vs,vx,vy,x) (в нашем примере – с-кубическому полиному interp(vsс,q_а,nус_а,q)), причем в скобках последнее q может принимать как значения компонент q_а вектора q_а (в этом случае выдается значение iс(q_а)), так и любые промежуточные значения q_П между значениями компонент вектора q_а – в этом случае выдается интерполирующее значение функции iс(q_П)).

  4.  Введите для q над графиком присвоение, например, в виде рядной переменной, обеспечивающей нужное число точек в промежутке построения интерполирующей функции iс(q). Постройте график интерполирующей функции iс(q) (см.рис. 10.1) на рисунке, где расположены интерполяционные точки.

10.2. Оценка точности интерполирования

Рассмотрим возможности интерполяции на примере интерполяции sin(x)  в точках 1…5 рис. 10.3. Процедура формирования необходимых объектов в РДМ согласно этапов построения из разд. 10.1 представлена на рис. 10.2: (ха,уа), векторов вторых производных vsL, vsp и vsc ( рис.10.2, А и В),  интерполирующих функций iLs(х), ips(х), ics(х) ( рис. 10.2, Б). Первые три элемента вектора производных являются его заголовком, осталь–

Рис. 10.2. Формирование элементов рис. 10.3: А – точек 1…5 кривой уа(ха) и векторов vs;                                                 Б – точек х для интерполяционных кривых iLs(х), iрs(х), iсs(х). В – структура векторов vs

ные – значениями вторых производных в интерполяционных точках. Интерполяционные сплайны, линейный интерполятор  iL(x) и интерполируемая функция sin(x) представлены на рис. 10.3.

 

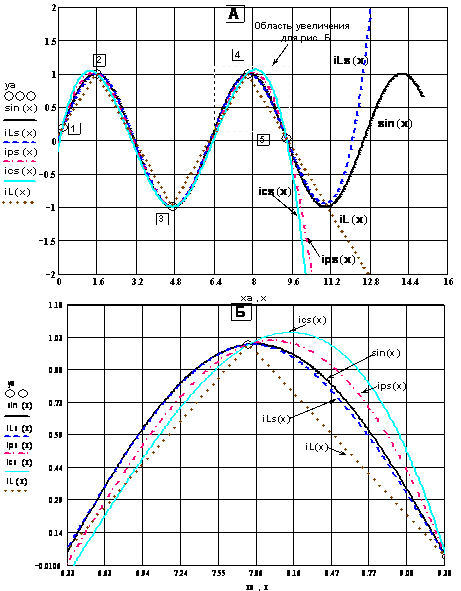
Рис. 10.3. Интерполяция в точках 1…5 кривой sin(x) в промежутке 0,2 £ х £ 9,4 линейным iL(x):= linterp(xa,ya,x) интерполятором и кубическими (iLs(x),  ips(x) и ics(x)) сплайнами из рис. 10.2

Из сравнения точности совпадения сплайн-кривых и sin(х) на рис.10.3 (в увеличенном масштабе на рис. 10.3, Б) следует хорошая аппроксимирующая способность интерполирующих кубических сплайнов пакета Mathcad:  наиболее точно аппроксимирует sin(x) сплайн iLs(х). Конкретные значения абсолютных погрешностей интерполяции приведены в табл. 10.1. Данные показывают, что погрешность интерполяции на большей части  диапазона аргумента у сплайна iLs(х) меньше в несколько раз, чем у сплайна iрs(х), погрешность которого в свою очередь в 2…3 раза меньше, чем у iсs(х). Таким образом, для функций с плавно меняющейся первой производной в диапазоне ±d (±1 для sin(х) рис. 10.3) наилучшая интерполяция у сплайна iLs(х). Линейный интерполятор iL(х) аппроксимирует sin(х) хуже, чем сплайны (см. рис. 10.3, Б).