
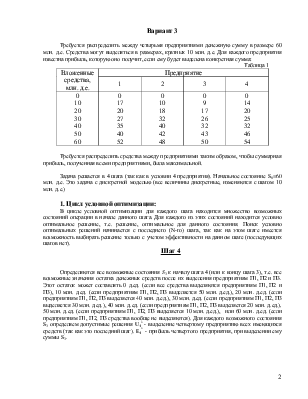

переходит операция распределения средств в результате принятия каждого решения (после выделения средств первому, второму и третьему предприятию), S3=S2-U3. Для каждого состояния S3 по таблице решения шага 4 находим условно-оптимальное значение критерия эффективности для четвертого шага, т.е. прибыль четвертого предприятия E4* от выделенных ему средств в размере S3. Находим критерий эффективности операции на третьем и четвертом шаге (суммарная прибыль третьего и четвертого предприятий) E3=Z3+ E4*. По максимальному значению E3 находим условно-оптимальное значение критерия эффективности для третьего и четвертого шагов – U3*. Здесь U3* - денежные средства, которые следует выделить предприятию П3 при наличии суммы S2. E3* - условно оптимальный критерий эффективности для предприятий П3 и П4, т.е. прибыль, получаемая этими предприятиями в результате решения U3*.
Таблица 3
|
S2 |
U3 |
Z3 |
S3 |
E4* |
E3 |
U3* |
E3* |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
10 |
0 10 |
0 9 |
10 0 |
14 0 |
14 9 |
0 |
14 |
|
20 |
0 10 20 |
0 9 17 |
20 10 0 |
20 14 0 |
20 23 17 |
10 |
23 |
|
30 |
0 10 20 30 |
0 9 17 26 |
30 20 10 0 |
25 20 14 0 |
25 29 31 26 |
20 |
31 |
|
40 |
0 10 20 30 40 |
0 9 17 26 32 |
40 30 20 10 0 |
32 25 20 14 0 |
32 34 37 40 32 |
30 |
40 |
|
50 |
0 10 20 30 40 50 |
0 9 17 26 32 43 |
50 40 30 20 10 0 |
46 32 25 20 14 0 |
46 41 42 46 46 43 |
0 |
46 |
|
60 |
0 10 20 30 40 50 60 |
0 9 17 26 32 43 50 |
60 50 40 30 20 10 0 |
54 46 32 25 20 14 0 |
54 55 49 51 52 57 50 |
50 |
57 |
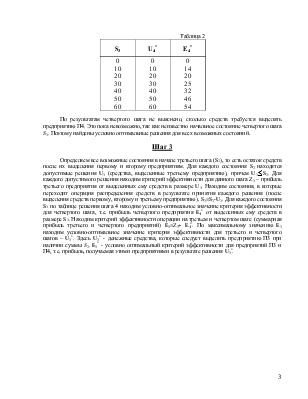
Шаг 2
Находим всевозможные состояния в начале второго шага (S1) – остаток средств после их выделения первому предприятию. Для каждого из них находим все допустимые решения U2. Для каждого решения находится критерий эффективности для данного шага Z2 – прибыль второго предприятия от выделения ему средств в размере U2. Находим состояния, в которые переходит операция распределения средств в результате принятия каждого решения (остатки средств после их выделения первому и второму предприятиям): S2=S1-U2. Для каждого состояния S2 по таблице из шага 3 находим условно-оптимальное значение критерия эффективности для третьего шага E3* - прибыль четвертого и третьего предприятий при условии, что им будет выделена сумма S2. Находим критерий эффективности на втором и третьем шаге (суммарная прибыль второго, третьего и четвертого предприятий), соответствующий каждому состоянию S1 и решению U2: E2=Z2+E3*. ПО максимальному значению E2 для каждого состояния S1 находится условно-оптимальное значение критерия эффективности для второго, третьего и четвертого шагов E2*. Здесь U2* - средства, которые следует выделить второму предприятию, если имеется сумма в размере S1; E2* - суммарная прибыль второго, третьего и четвертого предприятий, при условии, что сумма S1 будет разделена между ними оптимальным образом.
Таблица 4
|
S1 |
U2 |
Z2 |
S2 |
E3* |
E2 |
U2* |
E2* |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
10 |
0 10 |
0 10 |
10 0 |
14 0 |
14 10 |
0 |
14 |
|
20 |
0 10 20 |
0 10 18 |
20 10 0 |
23 14 0 |
23 24 18 |
10 |
24 |
|
30 |
0 10 20 30 |
0 10 18 32 |
30 20 10 0 |
31 23 14 0 |
31 33 32 32 |
10 |
33 |
|
40 |
0 10 20 30 40 |
0 10 18 32 40 |
40 30 20 10 0 |
40 31 23 14 0 |
40 41 41 46 40 |
30 |
46 |
|
50 |
0 10 20 30 40 50 |
0 10 18 32 40 42 |
50 40 30 20 10 0 |
46 40 31 23 14 0 |
46 50 49 55 54 42 |
30 |
55 |
|
60 |
0 10 20 30 40 50 60 |
0 10 18 32 40 42 48 |
60 50 40 30 20 10 0 |
57 46 40 31 23 14 0 |
57 56 58 63 63 56 48 |
30 |
63 |
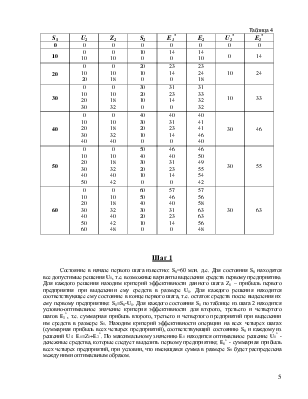
Шаг 1
Состояние в начале первого шага известно: S0=60 млн. д.е. Для состояния S0 находятся все допустимые решения U1, т.е. возможные варианты выделения средств первому предприятию. Для каждого решения находим критерий эффективности данного шага Z1 – прибыль первого предприятия при выделении ему средств в размере U1. Для каждого решения находится соответствующее ему состояние в конце первого шага, т.е. остаток средств после выделения их ему первому предприятию: S1=S0-U1. Для каждого состояния S1 по таблице из шага 2 находится условно-оптимальное значение критерия эффективности для второго, третьего и четвертого шагов E2*, т.е. суммарная прибыль второго, третьего и четвертого предприятий при выделении им средств в размере S1. Находим критерий эффективности операции на всех четырех шагах (суммарная прибыль всех четырех предприятий), соответствующий состоянию S0 и каждому из решений U1: E1=Z1+E2*. По максимальному значению E1 находится оптимальное решение U1* - денежные средства, которые следует выделить первому предприятию; E1* - суммарная прибыль всех четырех предприятий, при условии, что имеющаяся сумма в размере
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.