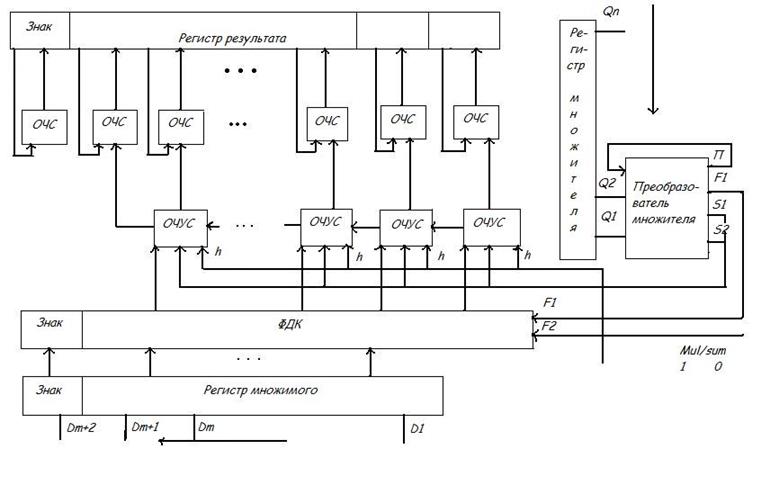
Рис.1
· Синтез одноразрядного четверичного сумматора.
ОЧС - это комбинационное устройство, имеющее 5 входов (2 разряда одного слагаемого, 2 разряда второго слагаемого и вход переноса) и 3 выхода. Принцип работы ОЧС описывается с помощью таблицы истинности (табл.4).
Разряды обоих слагаемых закодированы : 0 - 00; 1 - 01; 2 - 11; 3 - 10.
ОЧС синтезируется для схемы 2-го типа, поэтому безразличные наборы в таблице истинности отсутствуют.
Минимизацию переключательных функций проведем с помощью карт Карно и Вейча.
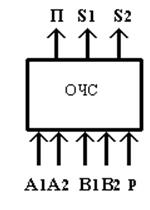
Таблица 4.
|
À1 |
À2 |
В1 |
В2 |
p |
П |
S1 |
S2 |
Пример операции в четверичной с/с |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0+0+0=00 |
|
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0+0+1=01 |
|
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0+1+0=01 |
|
|
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0+1+1=02 |
|
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0+3+0=03 |
|
|
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0+3+1=10 |
|
|
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0+2+0=02 |
|
|
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0+2+1=03 |
|
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1+0+0=01 |
|
|
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1+0+1=02 |
|
|
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1+1+0=02 |
|
|
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1+1+1=03 |
|
|
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1+3+0=10 |
|
|
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1+3+1=11 |
|
|
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1+2+0=03 |
|
|
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1+2+1=10 |
|
|
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
3+0+0=03 |
|
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
3+0+1=10 |
|
|
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
3+1+0=10 |
|
|
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
3+1+1=11 |
|
|
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
3+3+0=12 |
|
|
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
3+3+1=13 |
|
|
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
3+2+0=11 |
|
|
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
3+2+1=12 |
|
|
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
2+0+0=02 |
|
|
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
2+0+1=03 |
|
|
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
2+1+0=03 |
|
|
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
2+1+1=10 |
|
|
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
2+3+0=11 |
|
|
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
2+3+1=12 |
|
|
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
2+2+0=10 |
|
|
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
2+2+1=11 |
|
· Минимизация переключательных функций картами Карно-Вейча.
Для проведения минимизации переключательных функций необходимо выделить те наборы переменных, где функция принимает единичное значение.
4.1 Минимизация переключательной функции для S1:
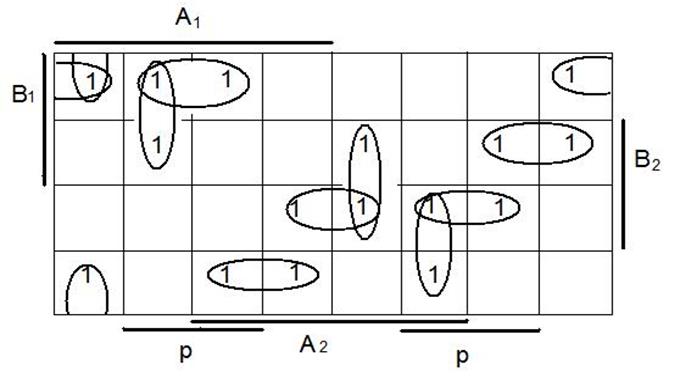
Следовательно, S1=a1
2
2
+b122+a1b12p+a1b12p+a1a212+1b2a2+1a2b2+
+1a21p+11b2p+1b1b22
Эффективность минимизации:
К=(16*5+16+5)/(10*4+10+4)=1.9
4.2 Минимизация переключательной функции для S2:
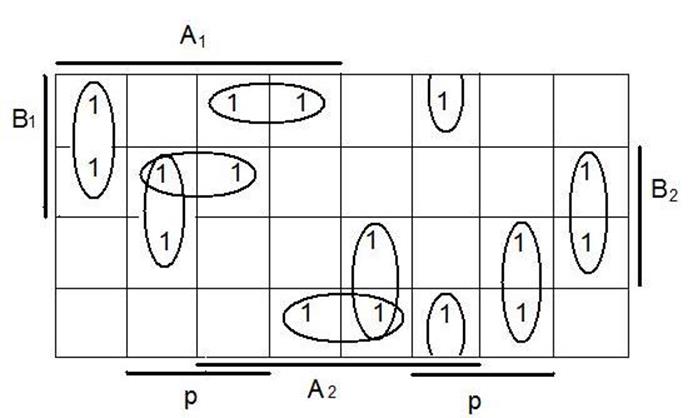
S2= a12b1 +a12 b2p+a1b1b2p+a1b12 a2+1 2a2 +11a2+12a2p+
+112p+1b22
Эффективность минимизации:
К=(16*5+16+5)/(9*4+9+4)=2
4.3 Минимизацию переключательной функции для П:
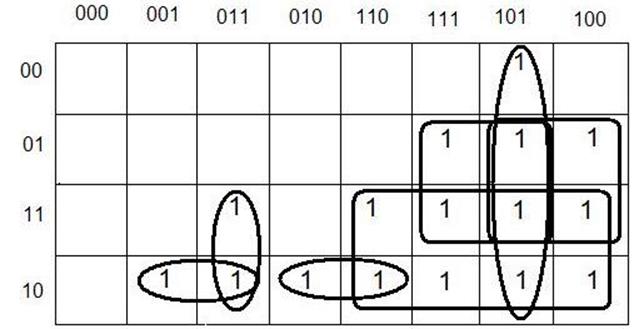
П=a121p+a11b2p+a12b2+a1b1+a2b1p+a2b12+b12p
Эффективность минимизации:
К=(16*5+16+5)/(23+7+4)=2.9
4.4 Функциональная схема ОЧС
(см. приложение 1)
4.5 Логический синтез ОЧС на мультиплексорах
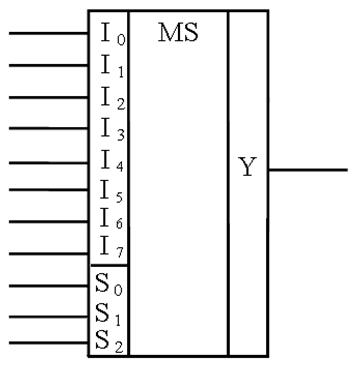
Рис. 2
Согласно заданию, ОЧС необходимо построить на мультиплексорах. Мультиплексор – это логическая схема, имеющая n информационных входов, m управляющих входов и один выход. При этом должно выполняться условие n=2m. На выход мультиплексора может быть пропущен без изменений любой (один) логический сигнал, поступающий на информационные входы. Порядковый номер информационного входа, значение с которого в данный момент должно быть передано на выход, определяется двоичным кодом на управляющих входах.
Для синтеза ОЧС используем функциональный базис, состоящий из элементов И, НЕ, ИЛИ (табл.5).
Таблица 5. ОЧС на мультиплексорах.
|
A1 A2B1 |
B2 P |
П |
S1 |
S2 |
I |
|
000 |
00 01 10 11 |
0 0 « 0» 0 0 |
0 0 0 В2Р 1 |
0 1 1 В2+Р 1 |
0 |
|
001 |
00 01 10 11 |
0 1 0 0 |
1 0 1 B2+ 1 |
0 0 1 B2 0 |
1 |
|
010 |
00 01 10 11 |
0 0 0 «0» 0 |
0 1 1 В2+Р 1 |
1 1 1 0 |
2 |
|
011 |
00 01 10 11 |
1 1 0 1 |
0 0 1 B2 0 |
0 1 0 0 |
3 |
|
100 |
00 01 10 11 |
0 1 1 B2+P 1 |
1 0 0 0 |
0 0 0 В2Р 1 |
4 |
|
101 |
00 01 10 11 |
1 1 1 «1» 1 |
1 1 0 1 |
1 0 1 B2+ 1 |
5 |
|
110 |
00 01 10 11 |
0 0 0 В2Р 1 |
1 1 1 0 |
1 0 0 0 |
6 |
|
111 |
00 01 10 11 |
1 1 1 «1» 1 |
0 1 0 0 |
1 1 0 1 |
7 |
Управляющее поле определяется тремя переменными: A1,A2,B1. На рис.3 показана функциональная схема ОЧС на мультиплексорах.
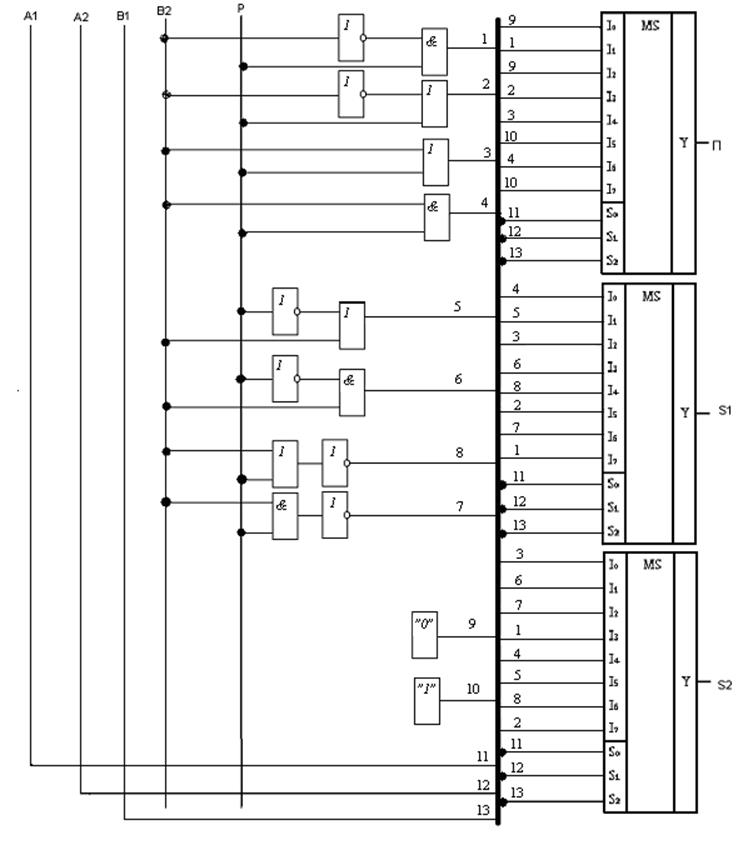
Рис. 3
Логический синтез одноразрядного четверичного умножителя - сумматора.
ОЧУС – это комбинационное устройство, имеющее шесть входов (два разряда из регистра множимого, два разряда из регистра множителя, вход переноса и управляющий вход h) и три выхода. Принцип работы ОЧУС представлен с помощью таблицы истинности (табл.6.).
Разряды множителя закодированы: 0 – 00; 1 – 01; 2 – 10; 3 – 11;
Разряды множимого закодированы: 0 – 00; 1 – 01; 2 – 11; 3 – 10;
Управляющий вход h определяет тип операции: 0 - умножение закодированных цифр, поступивших на информационные входы, и добавление переноса; 1 - вывод на выходы без изменения значения разрядов, поступивших из регистра множимого. В табл.6. выделено 36 безразличных наборов, так как на входы ОЧУС из разрядов множителя не может поступить код 11. При работе ОЧУС как сумматора на вход переноса не может поступить единица, а при умножении на ноль или единицу на вход переноса также не может поступить единица.
Таблица.6.
|
Пер |
Мн |
Мт |
Упр |
Перенос |
Результат |
Результат операции в четверичной с/с |
|||
|
Р1 |
X1 |
X2 |
Y1 |
Y2 |
h |
P |
Q1 |
Q2 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0*0+0=00 |
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
Выход – код «00» |
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0*1+0=00 |
|
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
Выход – код «00» |
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0*2+0=00 |
|
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
Выход – код «00» |
|
0 |
0 |
0 |
1 |
1 |
0 |
X |
X |
X |
0*3+0=00 |
|
0 |
0 |
0 |
1 |
1 |
1 |
X |
X |
X |
Выход – код «00» |
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1*0+0=00 |
|
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
Выход – код «01» |
|
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1*1+0=01 |
|
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
Выход – код «01» |
|
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1*2+0=02 |
|
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
Выход – код «01» |
|
0 |
0 |
1 |
1 |
1 |
0 |
X |
X |
X |
1*3+0=03 |
|
0 |
0 |
1 |
1 |
1 |
1 |
X |
X |
X |
Выход – код «01» |
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
3*0+0=00 |
|
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
Выход – код «03» |
|
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
3*1+0=03 |
|
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
Выход – код «03» |
|
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
3*2+0=12 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
Выход – код «03» |
|
0 |
1 |
0 |
1 |
1 |
0 |
X |
X |
X |
3*3+0=21 |
|
0 |
1 |
0 |
1 |
1 |
1 |
X |
X |
X |
Выход – код «03» |
|
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
2*0+0=00 |
|
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
Выход – код «02» |
|
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
2*1+0=02 |
|
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
Выход – код «02» |
|
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
2*2+0=10 |
|
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
Выход – код «02» |
|
0 |
1 |
1 |
1 |
1 |
0 |
X |
X |
X |
2*3+0=12 |
|
0 |
1 |
1 |
1 |
1 |
1 |
X |
X |
X |
Выход – код «02» |
|
1 |
0 |
0 |
0 |
0 |
0 |
X |
X |
X |
0*0+1=01 |
|
1 |
0 |
0 |
0 |
0 |
1 |
X |
X |
X |
Выход – код «00» |
|
1 |
0 |
0 |
0 |
1 |
0 |
X |
X |
X |
0*1+1=01 |
|
1 |
0 |
0 |
0 |
1 |
1 |
X |
X |
X |
Выход – код «00» |
|
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0*2+1=01 |
|
1 |
0 |
0 |
1 |
0 |
1 |
X |
X |
X |
Выход – код «00» |
|
1 |
0 |
0 |
1 |
1 |
0 |
X |
X |
X |
0*3+1=01 |
|
1 |
0 |
0 |
1 |
1 |
1 |
X |
X |
X |
Выход – код «00» |
|
1 |
0 |
1 |
0 |
0 |
0 |
X |
X |
X |
1*0+1=01 |
|
1 |
0 |
1 |
0 |
0 |
1 |
X |
X |
X |
Выход – код «01» |
|
1 |
0 |
1 |
0 |
1 |
0 |
X |
X |
X |
1*1+1=02 |
|
1 |
0 |
1 |
0 |
1 |
1 |
X |
X |
X |
Выход – код «01» |
|
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1*2+1=03 |
|
1 |
0 |
1 |
1 |
0 |
1 |
X |
X |
X |
Выход – код «01» |
|
1 |
0 |
1 |
1 |
1 |
0 |
X |
X |
X |
1*3+1=10 |
|
1 |
0 |
1 |
1 |
1 |
1 |
X |
X |
X |
Выход – код «01» |
|
1 |
1 |
0 |
0 |
0 |
0 |
X |
X |
X |
3*0+1=01 |
|
1 |
1 |
0 |
0 |
0 |
1 |
X |
X |
X |
Выход – код «03» |
|
1 |
1 |
0 |
0 |
1 |
0 |
X |
X |
X |
3*1+1=10 |
|
1 |
1 |
0 |
0 |
1 |
1 |
X |
X |
X |
Выход – код «03» |
|
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
3*2+1=13 |
|
1 |
1 |
0 |
1 |
0 |
1 |
X |
X |
X |
Выход – код «03» |
|
1 |
1 |
0 |
1 |
1 |
0 |
X |
X |
X |
3*3+1=22 |
|
1 |
1 |
0 |
1 |
1 |
1 |
X |
X |
X |
Выход – код «03» |
|
1 |
1 |
1 |
0 |
0 |
0 |
X |
X |
X |
2*0+1=01 |
|
1 |
1 |
1 |
0 |
0 |
1 |
X |
X |
X |
Выход – код «02» |
|
1 |
1 |
1 |
0 |
1 |
0 |
X |
X |
X |
2*1+1=03 |
|
1 |
1 |
1 |
0 |
1 |
1 |
X |
X |
X |
Выход – код «02» |
|
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
2*2+1=11 |
|
1 |
1 |
1 |
1 |
0 |
1 |
X |
X |
X |
Выход – код «02» |
|
1 |
1 |
1 |
1 |
1 |
0 |
X |
X |
X |
2*3+1=13 |
|
1 |
1 |
1 |
1 |
1 |
1 |
X |
X |
X |
Выход – код «02» |
Минимизируем ОЧУС при помощи алгоритма Рота
4.7 Минимизация функции Q1:
Множество единичных кубов:
L={001100, 010001, 010010, 010011, 010100, 010101, 011001,011010, 011011, 011101, 101100, 110100}
Множество безразличных кубов:
N={000110, 000111, 001110, 001111, 010110, 010111, 011110, 011111, 100000, 100001,100010,100011, 100101, 100110, 100111,101000, 101001,101010, 101011, 101101, 101110, 101111, 110000, 110001, 110010, 110011, 110101, 110110, 110111, 111000, 111001, 111010, 111011, 111101, 111110, 111111}.
Сначала склеим множество безразличных кубов N при помощи карты Карно: (рис4.)
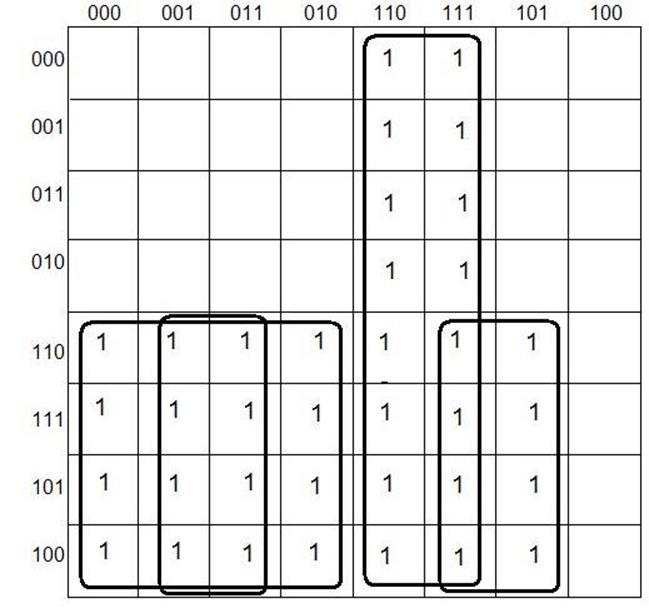
Рис4
После минимизации получили:
N=
.
Сформируем множество 
Первым этапом алгоритма Рота является нахождение множества простых импликант. Для реализации этого этапа используется операция умножения (*) над множествами C0, C1 и т.д.
Первый шаг умножения приведен в таблице 6.
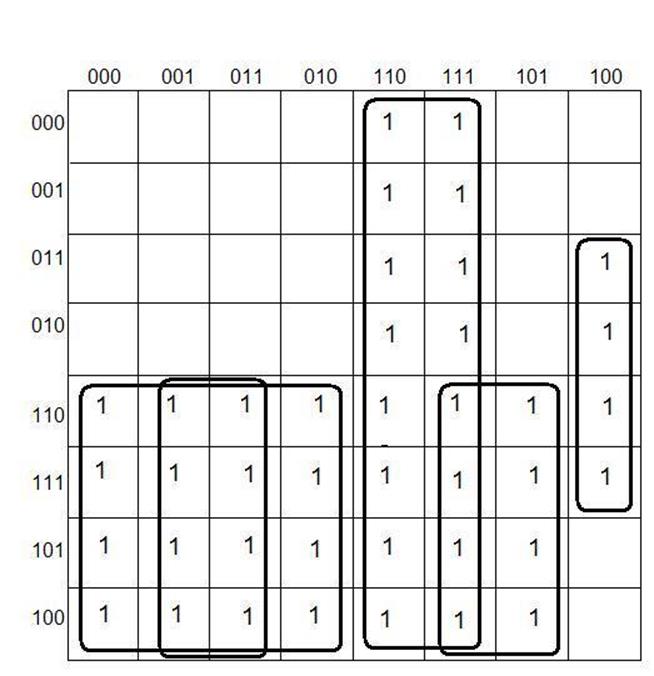
Р2={1xx0xx, xxx11x, 1xxxx1, x1x100}
Эффективность минимизации:
К=(40*6+40+6)/(10+4+3)=15.6
4.10 Функциональная схема ОЧУС
(приложение 2)
Преобразователь множителя (ПМ) служит для исключения
из множителя диад 11, заменяя их на триады 
.
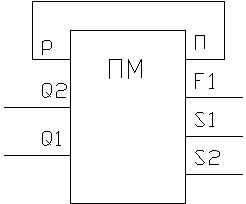
Схематическое изображение ПМ.
Таблица истинности ПМ.
|
Входы ПМ |
Выходы ПМ |
||||||
|
Q1 |
Q2 |
p |
П |
F1 |
S1 |
S2 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
|
|
0 |
1 |
1 |
0 |
0 |
1 |
0 |
|
|
1 |
0 |
0 |
0 |
0 |
1 |
0 |
|
|
1 |
0 |
1 |
1 |
1 |
0 |
1 |
|
|
1 |
1 |
0 |
1 |
1 |
0 |
1 |
|
|
1 |
1 |
1 |
1 |
0 |
0 |
0 |
|
5.1. Минимизация функций выходов ПМ.
Минимизируем функции выхода с использованием карт Вейча от трех переменных.
Минимизация Q 1:
П = Q 1 p + Q 2 Q 1
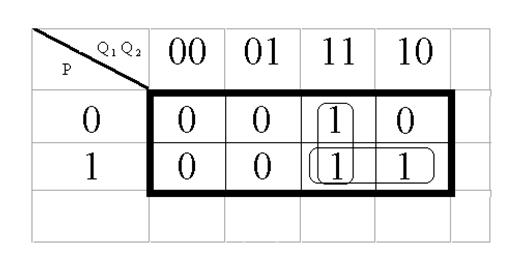
Минимизация Q 2:
F1= Q 1 Q 2 p + Q 1 Q 2 p
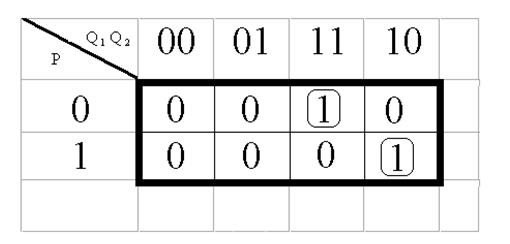
Минимизация S1:
S1 = Q 1
Q 2 p + Q 1 Q 2 p
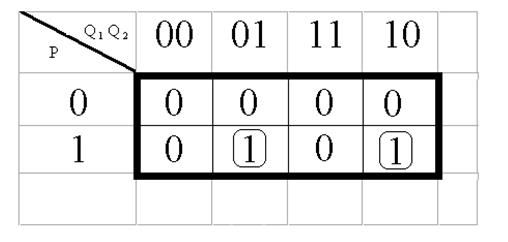
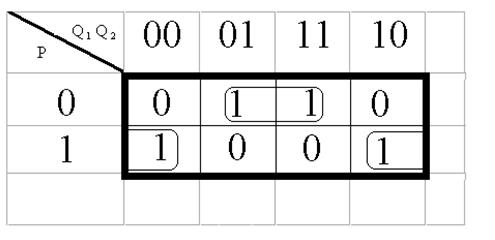
Минимизация S2:
S2 = Q 2 p + Q 2 p
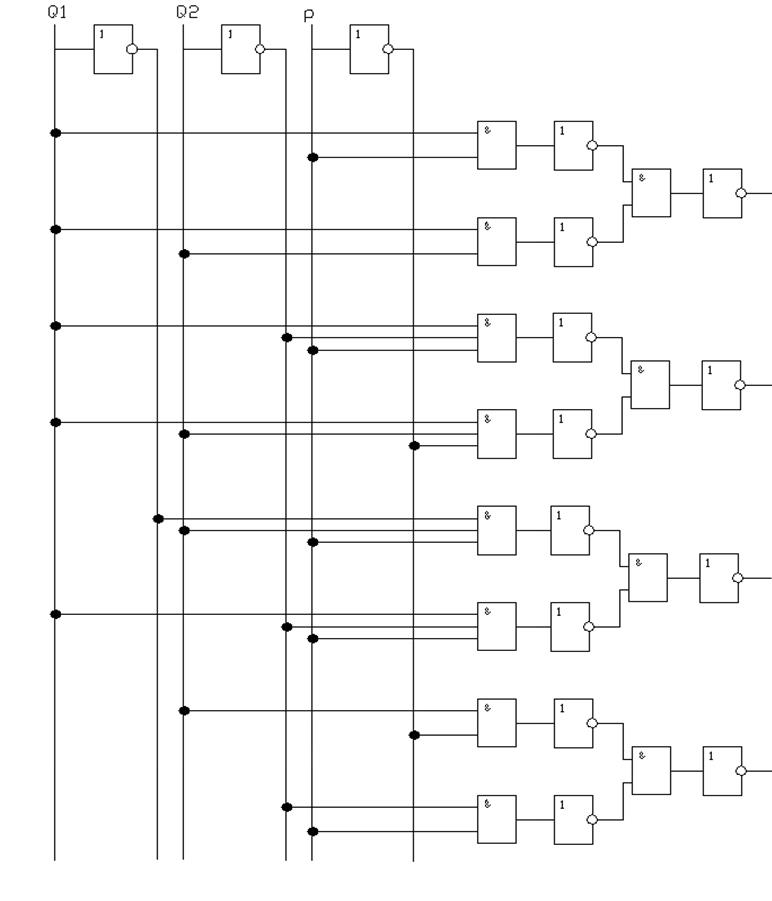
5.2. Функциональная схема ПМ.
Функциональная схема ПМ, построенная в логическом базисе А4, изображена на рис. 6.
П
F1
S1
S2
Рис. 6. Функциональная схема ПМ.
Временные затраты на умножение сомножителей определяются в основном затратами на образование частичных произведений, получаемых на выходах ОЧУС, и примерно равны:
Т=tсх+tочус+takk+tочс+Зочс+tфдк,
где tпм – время работы ПМ, tочс - время работы ОЧС, tочус - время работы ОЧУС, Зочс - время, затрачиваемое на ожидание единицы переноса во всех ОЧС, tакк – время работы регистра результата, tсх - время задержки в схеме
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
P
