Информатика и выч. техника \ Арифметические и логические основы вычислительной техники

Разработка сумматора-умножителя (Пояснительная записка)

Страницы работы

33 страницы (Word-файл)

Посмотреть все страницы

Скачать файл

Фрагмент текста работы

Согласно заданию, ОЧС необходимо построить на мультиплексорах. Мультиплексор – это логическая схема, имеющая n информационных входов, m управляющих входов и один выход. При этом должно выполняться условие n = 2^m.На выход мультиплексора может быть пропущен без изменений любой (один) логический сигнал, поступающий на информационные входы. Порядковый номер информационного входа, значение с которого в данный момент должно быть передано на выход, определяется двоичным кодом на управляющих входах.

Для синтеза ОЧС используем функциональный базис, состоящий из элементов И, НЕ, ИЛИ (табл.4)

Таблица. 4 ОЧС на мультиплексорах

A₁ A₂B₁

B₂P

S₁

S₂

000

0 « 0»

0 В2Р

1 В2+Р

001

1 P

1 B2+

1 B2

010

0 «0»

1 В2+Р

₁

₀

₂

011

0 +P

1 B2

0 P

100

1 B2+P

0 В2Р

101

1 «1»

0 +P

1 B2+

110

0 В2Р

111

1 «1»

0 P

0 +P

9. Функциональная схема ОЧС на мультиплексорах

Управляющее поле определяется тремя переменными: A₁,A₂,B₁. На рис.5 показана функциональная схема ОЧС на мультиплексорах.

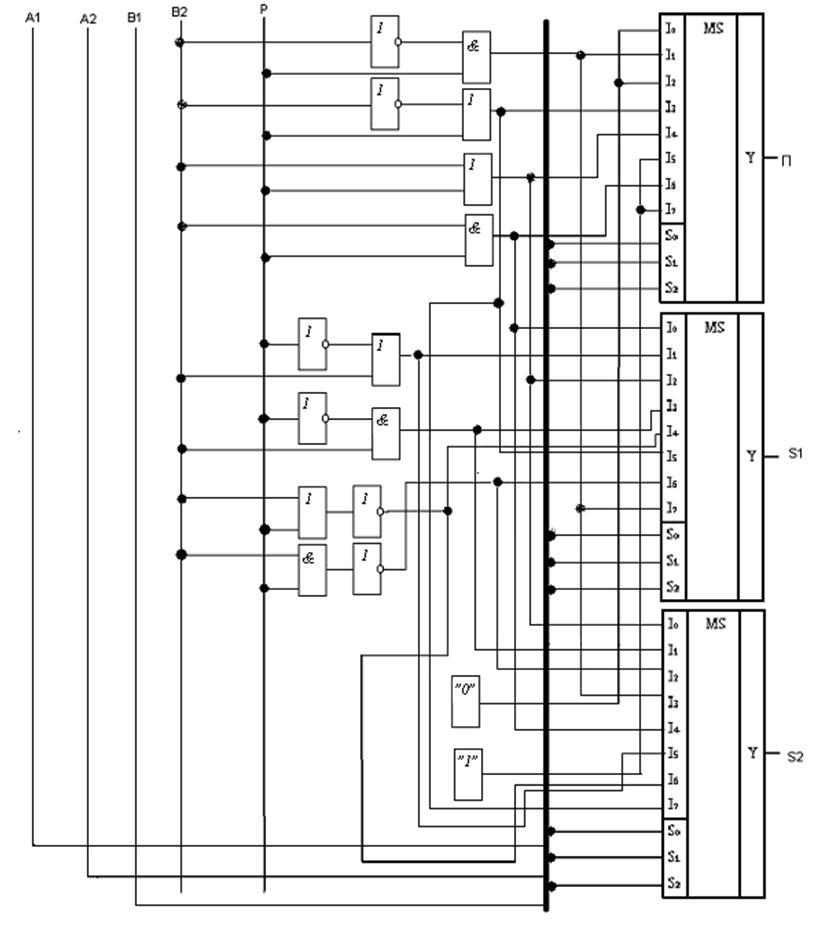
Рис. 5

10. ЛОГИЧЕСКИЙ СИНТЕЗ ОДНОРАЗРЯДНОГО ЧЕТВЕРИЧНОГО

УМНОЖИТЕЛЯ

ОЧУ - это комбинационное устройство, имеющее 5 входов (2 разряда из регистра МН, 2 разряда из регистра Мт и управляющий вход h) и 4 выхода. Принцип работы ОЧУ описывается с помощью таблицы истинности (табл.5).

Разряды множителя закодированы : 0 - 00; 1 - 01; 2 - 10; 3 - 11.

Разряды множимого закодированы : 0 - 00; 1 - 01; 2 - 11; 3 - 10.

Управляющий вход h определяет тип операции: 0 - умножение закодированных цифр, поступивших на информационные входы; 1 - вывод на выходы без изменения значения разрядов, поступивших из регистра множимого.

В таблице выделено 8 безразличных наборов, т.к. на входы ОЧУ из разрядов множителя не может поступить код 11.

Таблица. 5

Мн		Мт		упр.	Старшие разряды		Младшие разряды		Пример операции
X1	X2	Y1	Y2	h	P1	P2	P3	P4	В четверичной с/с
0	0	0	0	0	0	0	0	0	0*0=00
0	0	0	0	1	0	0	0	0	выход - код «00»
0	0	0	1	0	0	0	0	0	0*1=00
0	0	0	1	1	0	0	0	0	выход - код «00»
0	0	1	0	0	0	0	0	0	0*2=00
0	0	1	0	1	0	0	0	0	Выход - код «00»
0	0	1	1	0	0	0	0	0	0*3=00
0	0	1	1	1	0	0	0	0	выход - код «00»
0	1	0	0	0	0	0	0	0	1*0=00
0	1	0	0	1	0	0	0	1	выход - код «01»
0	1	0	1	0	0	0	0	1	1*1=01
0	1	0	1	1	0	0	0	1	выход - код «01»
0	1	1	0	0	0	0	1	1	1*2=02
0	1	1	0	1	0	0	0	1	выход - код «01»
0	1	1	1	0	0	0	1	0	1*3=03
0	1	1	1	1	0	0	0	1	выход - код «01»
1	0	0	0	0	0	0	0	0	3*0=00
1	0	0	0	1	0	0	1	0	выход - код «03»
1	0	0	1	0	0	0	1	0	3*1=03
1	0	0	1	1	0	0	1	0	Выход - код «03»
1	0	1	0	0	0	1	1	1	3*2=10
1	0	1	0	1	0	0	1	0	выход - код «03»
1	0	1	1	0	1	1	0	1	3*3=21
1	0	1	1	1	0	0	1	0	выход - код «03»
1	1	0	0	0	0	0	0	0	2*0=00
1	1	0	0	1	0	0	1	1	выход - код «02»
1	1	0	1	0	0	0	1	1	2*1=02
1	1	0	1	1	0	0	1	1	выход - код «02»
1	1	1	0	0	0	1	0	0	2*2=10
1	1	1	0	1	0	0	1	1	Выход - код «02»
1	1	1	1	0	0	1	1	1	2*3=12
1	1	1	1	1	0	0	1	1	Выход - код «02»

Минимизируем ОЧУ при помощи алгоритма Рота:

10.1 Минимизация функции Р1:

Множество единичных кубов:

L={нету}

Множество безразличных кубов:

N={00110,00111,01110,01111,10110,10111,11110,11111}

Так как единичных кубов нету, то на выходе функции Р1получается константа нуля

10.2 Минимизация функции Р2:

Множество единичных кубов:

L={10100,11100}

Множество безразличных кубов:

N={00110,00111,01110,01111,10110,10111,11110,11111}

Сформируем множество

Первым этапом алгоритма Рота является нахождение множества простых импликант. Для реализации этого этапа используется операция умножения (*) над множествами C₀, C₁ и т.д.

Первый шаг умножения приведен в таблице 6.

Таблица 6 Поиск простых импликант(C₀* C₀)

C0*C0	10100	11100	00110	00111	01110	01111	10110	10111	11110	11111
10100	---------
11100	1x100	---------
00110			---------
00111			0011x	---------
01110			0x110		---------
01111				0x111	0111x	---------
10110	101x0		x0110				---------
10111				x0111			1011x	---------
11110		111x0			x1110		1x110		---------
11111						x1111		1x111	1111x	---------

С1={1x100, 101x0, 111x0, 0011x, 0x110, x0110, x0110,

x0111, 0111x, x1110, x1111, 1011x, 1x110, 1x111, 1111x }

Таблица 7. Поиск простых импликант(C₁* C₁)

C1*C1

1x100

101x0

111x0

0011x

0x110

x0110

0x111

x0111

0111x

x1110

x1111

1011x

1x110

1x111

1111x

1x100

--------

101x0

--------

111x0

1x1x0

--------

0011x

--------

0x110

--------

X0110

--------

0x111

0x11x

--------

X0111

x011x

--------

0111x

0x11x

--------

X1110

xx110

--------

X1111

xx111

x111x

--------

1011x

x011x

--------

1x110

1x1x0

xx110

--------

1x111

xx111

1x11x

--------

1111x

x111x

1x11x

--------

C2={ 1x1x0, 0x11x, x011x, xx110, xx111, x111x, 1x11x }

Таблица 8. Поиск простых импликант(C₂* C₂)

C2*C2	1x1x0	0x11x	x011x	xx110	xx111	x111x	1x11x
1x1x0
0x11x
X011x
xx110
xx111				xx11x
X111x			xx11x
1x11x		xx11x

C3={ xx11x } Z0 = {1x1x0}

Таблица 9. Поиск простых импликант(C₃* C₃)

C3*C3	xx11x
xx11x

Множество простых импликант z={1x1x0, xx11x}

Для поиска L-экстремалей на множестве простых импликант воспользуемся операцией вычитание (#)

Таблица 10. Поиск L-экстремалей

Z#(Z\z)	1x1x0	xx11x
1x1x0		0zzz1 0x11x xx111
xx11x	zzz0z 1x100

Таблица 11. Проверка L-экстремалей

L&^E	10100	11100
1x100	10100	11100
0x11x	Ø	Ø
xx111	Ø	Ø

Далее необходимо проанализировать, какие из исходных кубов множества L не покрыты найденными L-экстремалями

Таблица 12. Поиск непокрытых исходных наборов.

L#E

10100

11100

1x1x0

zzzzz

Множество простых импликант

E={1x1x0}

Р2=X1Y1

10.3 Минимизация функции Р3:

Множество единичных кубов:

L={01100,10001,10010,10011,10100,10101,11001,11010,11011,11101}

Множество безразличных кубов:

N={00110,00111,01110,01111,10110,10111,11110,11111}

Таблица 13. Поиск простых импликант(C₀* C₀)

C0*C0	01100	10001	10010	10011	10100	10101	11001	11010
01100	----------
10001		----------
10010			----------
10011		100x1	1001x	----------
10100					----------
10101		10x01			1010x	----------
11001		1x001					----------
11010			1x010					----------
11011				1x011			110x1	1101x
11101						1x101	11x01
00110
00111
01110	011x0
01111
10110			10x10		101x0
10111				10x11		101x1
11110								11x10
11111

Таблица 13(Продолжение). Поиск простых импликант(C₀* C₀)

C0*C0	11011	11101	00110	00111	01110	01111	10110	10111	11110	11111
01100
10001
10010
10011
10100
10101
11001
11010
11011	----------
11101		----------
00110			----------
00111			0011x	----------
01110			0x110		----------
01111				0x111	0111x	----------
10110			x0110				----------
10111				x0111			1011x	----------
11110					x1110		1x110		----------
11111	11x11	111x1				x1111		1x111	1111x	----------

C1= {011x0, 100x1, 10x01, 1x001, 1001x, 1x010, 10x10, 1x011, 10x11, 1010x,

101x0, 1x101, 101x1, 110x1, 11x01, 1101x, 11x10, 11x11, 111x1, 0011x,

0x110, x0110, 0x111, x0111, 0111x, x1110, x1111, 1011x, 1x110, 1x111, 1111x}

Таблица 14. Поиск простых импликант(C₁* C₁)

C1*C1

011x0

100x1

10x01

1x001

1001x

1x010

10x10

1x011

10x11

1010x

101x0

1x101

101x1

110x1

11x01

1101x

11x10

011x0

--------

100x1

--------

10x01

--------

1x001

--------

1001x

--------

1x010

--------

10x10

--------

1x011

1x0x1

1x01x

--------

10x11

10xx1

10x1x

--------

1010x

--------

101x0

--------

1x101

1xx01

--------

101x1

10xx1

101xx

--------

110x1

1x0x1

--------

11x01

1xx01

--------

1101x

1x01x

--------

11x10

1xx10

--------

11x11

1xx11

11xx1

11x1x

111x1

1x1x1

11xx1

0011x

0x110

x0110

0x111

x0111

0111x

x1110

x1111

1011x

10x1x

101xx

1x110

1xx10

1x111

1xx11

1x1x1

1111x

11x1x

Таблица 14(Продолжение). Поиск простых импликант(C₁* C₁)

C1*C1

11x11

111x1

0011x

0x110

x0110

0x111

x0111

0111x

x1110

x1111

1011x

1x110

1x111

1111x

011x0

100x1

10x01

1x001

1001x

1x010

10x10

1x011

10x11

1010x

101x0

1x101

101x1

110x1

11x01

1101x

11x10

11x11

--------

111x1

--------

0011x

--------

0x110

--------

x0110

--------

0x111

0x11x

--------

x0111

x011x

--------

0111x

0x11x

--------

x1110

xx110

--------

x1111

xx111

x111x

--------

1011x

x011x

--------

1x110

xx110

--------

1x111

xx111

1x11x

--------

1111x

x111x

1x11x

--------

C2 = { 11xx1; 1xx01; 1x1x1; 1x01x; 11x1x; 1x0x1; 1xx11; 1xx10;

101xx; 10xx1; 10x1x; 1x11x; x111x; xx111; xx110; x011x; 0x11x }

Z1 = { 011x0 }

Таблица 15. Поиск простых импликант(C₂* C₂)

C2*C2

10xx1

1x0x1

1xx01

1x01x

10x1x

1xx10

1xx11

101xx

1x1x1

11xx1

11x1x

0x11x

x011x

xx110

xx111

x111x

1x11x

10xx1

--------

1x0x1

--------

1xx01

--------

1x01x

--------

10x1x

--------

1xx10

--------

1xx11

1xxx1

1xx1x

--------

101xx

--------

1x1x1

1xxx1

--------

11xx1

1xxx1

--------

11x1x

1xx1x

--------

0x11x

--------

x011x

--------

xx110

--------

xx111

xx11x

--------

x111x

xx11x

--------

1x11x

1xx1x

xx11x

--------

C3 = { 1xxx1; 1xx1x; xx11x }

Z2 = { 011x0; 101xx }

Таблица 16. Поиск простых импликант(C₃* C₃)

C3*C3	1xxx1	1xx1x	xx11x
1xxx1	-------------
1xx1x		-------------
xx11x			-------------

Конечное множество простых импликант Z = { 011x0; 101xx; 1xxx1; 1xx1x; xx11x }

Поиск L-экстремалей.

Таблица 17. Поиск L-экстремалей

Z#(Z\z)	011x0	101xx	1xxx1	1xx1x	xx11x
011x0		yyzz1 101xx	y00zy 1xxx1	y00z1 1xx1x	10zz1 1x11x x011x xx111
101xx	yyzzz 011x0		z10zz 11xx1 1x0x1	z10zz 11x1x 1x01x	z1zzz 1111x 0zzzz 0011x 01zzz 0x111 x1111
1xxx1	yzzzy 011x0	zzzz0 101x0		zzzz0 11x10 zzzz0 1x010	zzzz0 11110 yzzz0 0011x yzzzz 0x111 0zzzz 01111
1xx1x	yzz0z 011x0	zzz0z 10100	zzz0z 11x01 zzz0z 1x001		zzzzz Ø yzzzz 0011x yzzzz 0x111 yzzzz 01111
xx11x	zzz0z 01100	zzzyz 10100	zz0yz 11x01 zzyyz 1x001	zz0zz 11010 zzyzz 1x010

Удаление лишних L-экстремалей

Таблица 18. Удаление лишних L-экстремалей

L&^E	01100	10001	10010	10011	10100	10101	11001	11010	11011	11101
01100	01100	Ø	Ø	Ø	Ø	Ø	Ø	Ø	Ø	Ø
10100	Ø	Ø	Ø	Ø	10100	Ø	Ø	Ø	Ø	Ø
11x01	Ø	Ø	Ø	Ø	Ø	Ø	11001	Ø	Ø	11101
1x001	Ø	10001	Ø	Ø	Ø	Ø	11001	Ø	Ø	Ø
11010	Ø	Ø	Ø	Ø	Ø	Ø	Ø	11010	Ø	Ø
1x010	Ø	Ø	10010	Ø	Ø	Ø	Ø	11010	Ø	Ø
0011x	Ø	Ø	Ø	Ø	Ø	Ø	Ø	Ø	Ø	Ø
0x111	Ø	Ø	Ø	Ø	Ø	Ø	Ø	Ø	Ø	Ø
01111	Ø	Ø	Ø	Ø	Ø	Ø	Ø	Ø	Ø	Ø

Множество L-экстремалей E = { 011x0; 101xx; 1xxx1; 1xx1x }

Таблица 19 .Покрытие оставшихся кубов

L#E	01100	10001	10010	10011	10100	10101	11001	11010	11011	11101
011x0	zzzzz Ø	yyyzy 10001	yyyzz 10010	yyyzy 10011	yyzzz 10100	yyzzy 10101	yzyzy 11001	yzyzz 11010	yzyzy 11011	yzzzy 11101
101xx		zzyzz 10001	zzyzz 10010	zzyzz 10011	zzzzz Ø	zzzzz Ø	zyyzz 11001	zyyzz 11010	zyyzz 11011	zyzzz 11101
1xxx1		zzzzz Ø	zzzzy 10010	zzzzz Ø			zzzzz Ø	zzzzy 11010	zzzzz Ø	zzzzz Ø
1xx1x			zzzzz Ø					zzzzz Ø

Минимальное покрытие - множество L-экстремалей E = { 011x0; 101xx; 1xxx1; 1xx1x }

Р3=x2y1+ x1y1+x1h+x1y2

10.4 Минимизация функции Р4:

Множество единичных кубов:

L={01001, 01010, 01011, 01100, 01101, 10100, 11001, 11010, 11011, 11101 }

Множество безразличных кубов:

N={00110,00111,01110,01111,10110,10111,11110,11111}

Таблица 20. Поиск простых импликант(C₀* C₀)

C0*C0	01001	01010	01011	01100	01101	10100	11001	11010	11011	11101	00110	00111	01110	01111	10110	10111	11110	11111
01001	--------
01010		--------
01011	010x1	0101x	--------
01100				--------
01101	01x01			0110x	--------
10100						--------
11001	x1001						--------
11010		x1010						--------
11011			x1011				110x1	1101x	--------
11101					x1101		11x01			--------
00110											--------
00111											0011x	--------
01110		01x10		011x0							0x110		--------
01111			01x11		011x1							0x111	0111x	--------
10110						101x0					x0110				--------
10111												x0111			1011x	--------
11110								11x10					x1110		1x110		--------
11111									11x11	111x1				x1111		1x111	1111x	--------

C1 = { 11x01; x1101; 111x1; 1101x; 110x1; x1011; 11x11; x1010; 11x10; x1001;

101x0; 0110x; 01x01; 011x1; 011x0; 0101x; 010x1; 01x11; 01x10; 0011x;

0x110; x0110; 0x111; x0111; 0111x; x1110; x1111; 1011x; 1x110; 1x111; 1111x }

Z0 = { Ø }

Таблица 21. Поиск простых импликант(C₁* C₁)

C1*C1

010x1

01x01

x1001

0101x

x1010

01x10

x1011

01x11

0110x

011x0

x1101

011x1

101x0

110x1

11x01

1101x

010x1

--------

01x01

--------

x1001

--------

0101x

--------

x1010

--------

01x10

--------

x1011

x10x1

x101x

--------

01x11

01xx1

01x1x

--------

0110x

--------

011x0

--------

x1101

x1x01

--------

011x1

01xx1

011xx

--------

101x0

--------

110x1

x10x1

--------

11x01

x1x01

--------

1101x

x101x

--------

11x10

x1x10

11x11

x1x11

11xx1

111x1

x11x1

11xx1

0011x

0x110

x0110

0x111

x0111

0111x

01x1x

011xx

x1110

x1x10

x1111

x1x11

x11x1

1011x

1x110

1x111

1111x

11x1x

Таблица 21(Продолжение). Поиск простых импликант(C₁* C₁)

1 2 3 4

Информация о работе

ВУЗ:

Белорусский государственный университет информатики и радиоэлектроники (БГУИР)

Предмет:

Арифметические и логические основы вычислительной техники

Тип:

Курсовые работы

Категория:

Информатика и выч. техника (Технические предметы)

Размер файла:

940 Kb

Скачали:

Скачать файл

Разработка сумматора-умножителя (Пояснительная записка)

Страницы работы

Фрагмент текста работы

9. Функциональная схема ОЧС на мультиплексорах

Z1 = { 011x0 }

C3 = { 1xxx1; 1xx1x; xx11x }

Z2 = { 011x0; 101xx }

Поиск L-экстремалей.

Таблица 17. Поиск L-экстремалей

Минимальное покрытие - множество L-экстремалей E = { 011x0; 101xx; 1xxx1; 1xx1x }

C1 = { 11x01; x1101; 111x1; 1101x; 110x1; x1011; 11x11; x1010; 11x10; x1001;

101x0; 0110x; 01x01; 011x1; 011x0; 0101x; 010x1; 01x11; 01x10; 0011x;

0x110; x0110; 0x111; x0111; 0111x; x1110; x1111; 1011x; 1x110; 1x111; 1111x }

Похожие материалы

Информация о работе