






БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТРАНСПОРТА
Электротехнический факультет
Кафедра «Электротехника»
РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА №3
по курсу «Теоретические основы электротехники»
Шифр: 794
|
Выполнил студент группы ЭТ-21 Шелег В.Н. |
Проверил преподователь Воронин А.В. |
2006
Задача №1
Исходные данные:
Uлm =440 B; ψu = 1200; ZЛ = 2+j2 Ом; Z1 = 16+j20 Ом; Z2 = 14-j18 Ом; Z3 = 10+j21 Ом;
Z4 = j19 Ом; Z5 = 21+j20 Ом; Z6 = 23+j15 Ом;
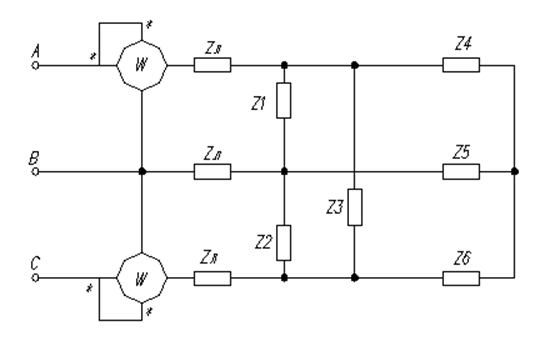
Расчётная схема:
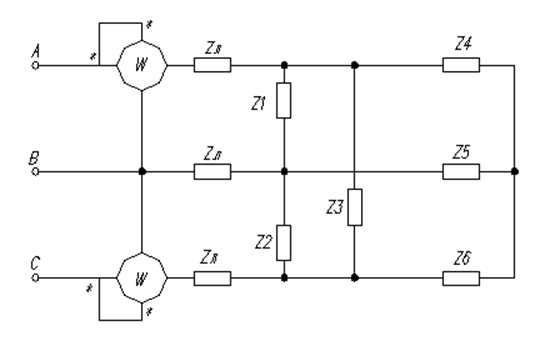
Рассчитать токи и напряжения на всех участках цепи:
Определение фазных ЭДС. Примем, что вектор фазы ЭДС «А» совпадает с осью действительных чисел. В этом случае ЭДС фаз источника питания в комплексной форме определяется следующим образом:
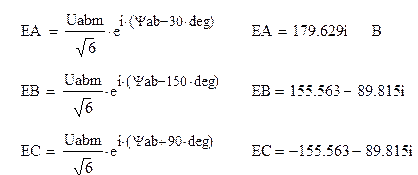
Следующим этапом расчёта является упрощение схемы. Заменим схему звезда с сопротивлениями (Z4, Z5, Z6,) на соединение треугольник
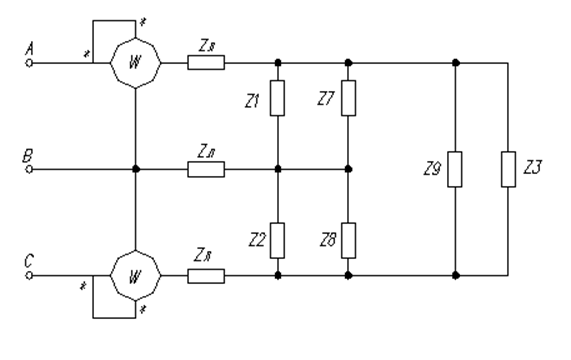
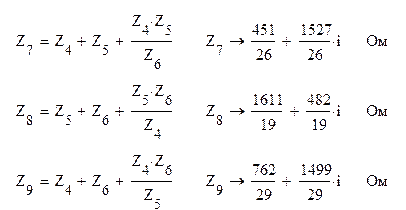
Сопротивления Z1-Z7, Z2-Z8, Z3-Z9 включены параллельно, значит
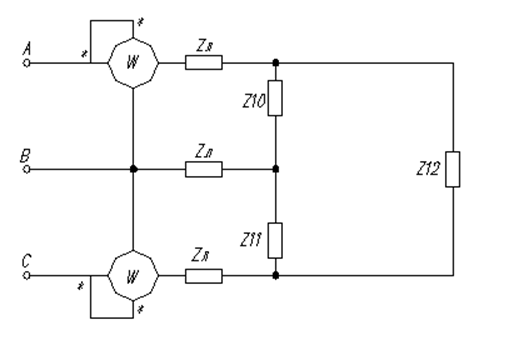
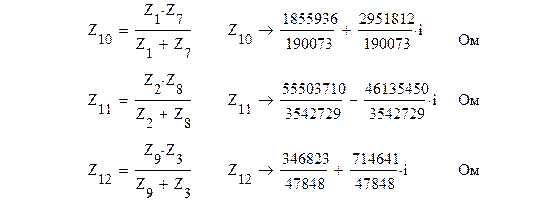
Схема ещё более упроститься, если треугольник сопротивлений Z10, Z11, Z12, заменить эквивалентной звездой
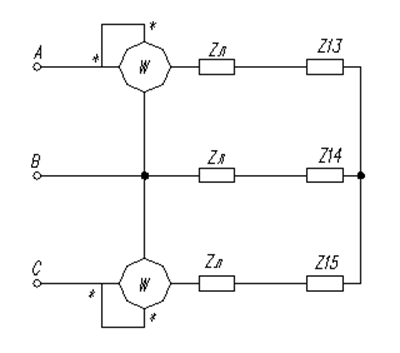
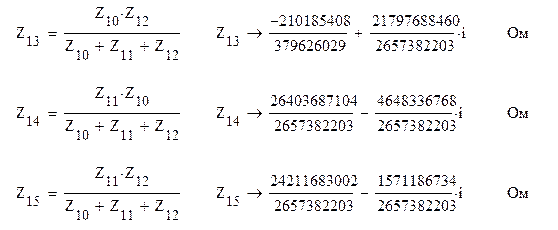
Сопротивления фазы нагрузки определяются суммированием линейного и результирующих сопротивлений Z13, Z14,Z15:
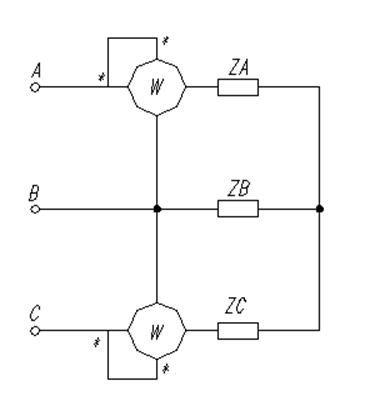
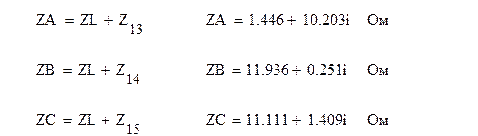
Напряжение смещения нейтрали определяется по выражению
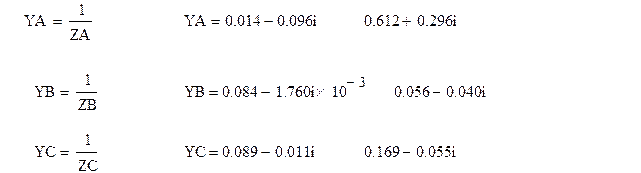
Напряжение на фазах нагрузки определяется следующим образом:
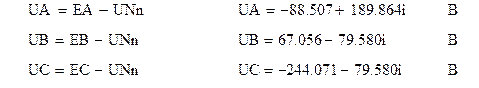
Линейные токи теперь легко определить по закону Ома:
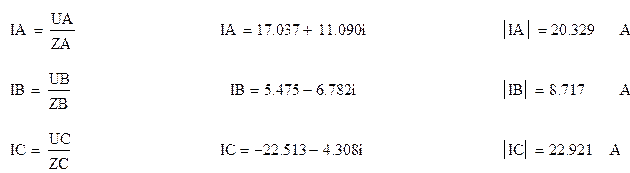
Правильность определения токов IA, IB, IC может быть проверена по первому закону Кирхгофа, составленному для узла «0»:
![]()
Токи в ветвях с сопротивлениями Z1, Z2, Z3 можно найти, используя закон Ома, если известны потенциалы точек 1,2,3. Заземляя точку 0 и приравнивая тем её потенциал к нулю, определяем комплексные потенциалы точек 1,2,3,4:
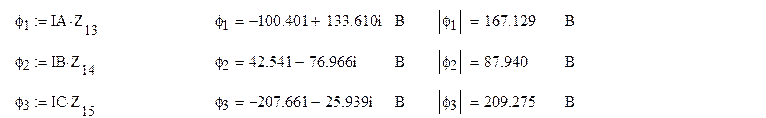
![]()
Токи в сопротивлениях нагрузки(Z1, Z2, Z3) определяются по закону Ома, а для (Z4, Z5, Z6) применим первый закон Кирхгофа:
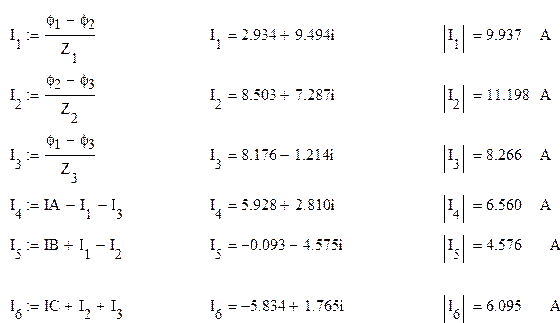
Найдём падение напряжения на каждом участке цепи:
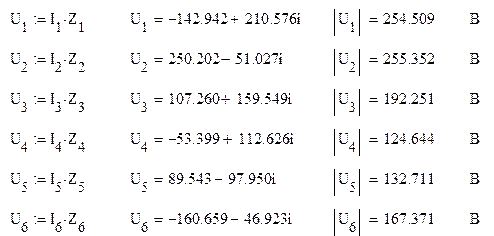
Проверка правильности расчётов
Правильность проведённых расчётов проверяется балансом мощности.
В цепях переменного тока баланс мощности определяется равенством комплекса полной мощности источника источника питания комплексу мощности потерь во всех сопротивлениях нагрузки.
Полная мощность трёхфазного источника питания, работающего в несимметричном режиме, равна сумме полных мощностей каждой фазы, определённых в комплексной форме:
![]()
где S∑ - комплекс полной мощности трёхфазного источника питания.
Следовательно, выражение баланса мощности системы имеет вид
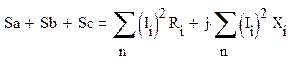
где ![]() ;
; ![]() ;
; ![]()
IA, IB, IC – комплексно сопряжённые значения токов IA, IB, IC; Ri, Xi – активное и реактивное сопротивление i-й ветви; Ii – действующее значение тока в ветви с номером i.Причём активное сопротивление всегда положительно, индуктивное сопротивление берётся со знаком плюс, а емкостное – со знаком минус.
Подставляя численные значения, получим
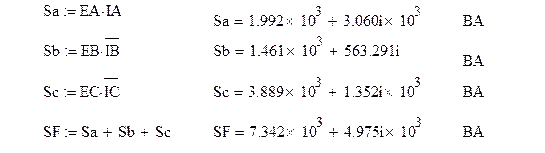
Мощность активных потерь определяется из выражения
![]()
![]()
Определяем мощность реактивных потерь:
![]()
![]()
Мощность источника питания S∑ и мощность потерь в сопротивлениях цепи ΔS совпадают:
SF=P + iQ
это говорит о том, что расчёт выполнен верно
Определим показания ваттметра:
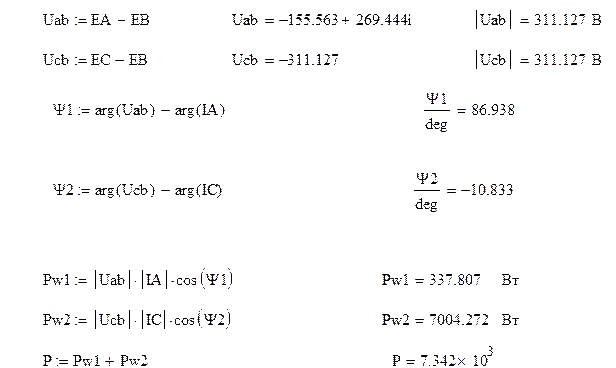
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.