БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТРАНСПОРТА
Электротехнический факультет
Кафедра «Электротехника»
РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА №6
по курсу «Теоретические основы электротехники»
Шифр: 821
|
Выполнил студент группы ЭС-31 Матылицкий И. В. |
Проверил ассистент Воронин А.В. |
2006
Задача №1.
Расчёт электростатического поля несоосных пераллельных цилиндров.
1. Для данной системы двух
параллельных цилиндров, имеющих равные заряды противоположного знака (![]() ), определить:
), определить:
а) ёмкость;
б) напряжение или заряд (в зависимости от варианта).
Поле считать плоскопараллельным.
2. Построить графическую картину электростатического поля, соблюдая следующие требования:
а) разность потенциалов между двумя любыми соседними линиями равного потенциала должна быть одна и та же;
б) поток вектора напряжённости электростатического поля во всех силовых трубках должен быть одинаков ;
в) при построении картины поля на каждой линии равного потенциала указать значение потенциала; на силовых линиях должно быть указано их направление и ограниченное данной линией значение потока напряжённости поля, отсчитываемое от некоторой фиксированной линии, принятой за начальную.
3. Вычислить и представить в виде графиков изменение потенцтала и напряжённости элктростатического поля на линии, соединяющей наиболее близкие точки цилиндров, и распределение плотности заряда на поверхности цилиндра меньшего радиуса.
Параметры расчёта:
![]()
![]()
![]()
Расчётный чертёж:
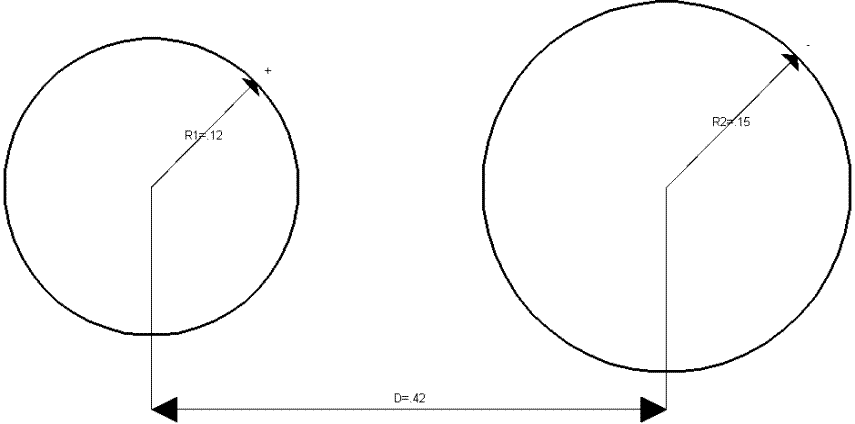
1. Для данной системы двух
параллельных цилиндров, имеющих равные заряды противоположного знака (![]() ),
определим:
),
определим:
а) ёмкость;
б) напряжение или заряд (в зависимости от варианта).
Поле считаем плоскопараллельным.
Расчитаем параметры ![]() и
и ![]() - расстояния между
позиционируемой осью Y
и центрами цилиндров.
- расстояния между
позиционируемой осью Y
и центрами цилиндров.
![h[1] = abs(1/2*(D^2-R[2]^2+R[1]^2)/D), h[2] = abs(1/2*(D^2+R[2]^2-R[1]^2)/D)](https://files3.vunivere.ru/workbase/00/03/70/14/images/image008.jpg)
![]()
Рассчитаем параметр b - расстояние между
осью Y и
электрическими осями цилиндров (расстояние одинаковое).
![sqrt(h[1]^2-R[1]^2) = .1604462049, sqrt(h[2]^2-R[2]^2) = .1604462051](https://files3.vunivere.ru/workbase/00/03/70/14/images/image010.jpg)
![sqrt(h[1]^2-R[1]^2) = sqrt(h[2]^2-R[2]^2)](https://files3.vunivere.ru/workbase/00/03/70/14/images/image011.jpg)
![]()
Построим чертёж с нанесёнными электрическими осями цилиндров, указанной осью Y и расчитанными выше параметрами.
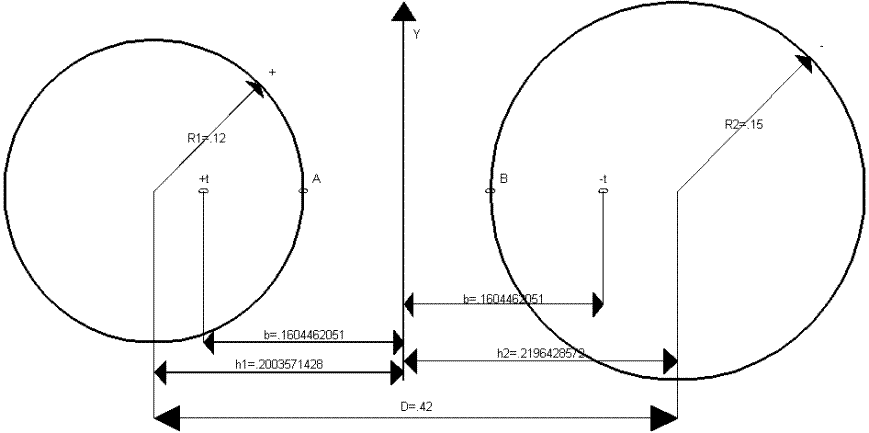
Определим параметры ![]() ,
,![]() ,
,![]() ,
,![]() - расстояния между точкой A и осями
- расстояния между точкой A и осями ![]() и
и ![]() , точкой B и осями
, точкой B и осями ![]() и
и ![]() , соответственно.
, соответственно.
![]()
![]()
Зададим формулу потенциал в точке A:
![phi[A] = 1/2*tau*ln(r[A-tau]/r[A+tau])/(Pi*epsilon[r]*epsilon[0])](https://files3.vunivere.ru/workbase/00/03/70/14/images/image023.jpg)
Зададим формулу потенциал
в точке B:
![phi[B] = 1/2*tau*ln(r[B-tau]/r[B+tau])/(Pi*epsilon[r]*epsilon[0])](https://files3.vunivere.ru/workbase/00/03/70/14/images/image024.jpg)
Зададим формулу разности
потенциалов между точками A и B:
![]()
![U = 1/2*tau*ln(r[A-tau]*r[B+tau]/(r[A+tau]*r[B-tau]))/(Pi*epsilon[r]*epsilon[0])](https://files3.vunivere.ru/workbase/00/03/70/14/images/image026.jpg)
Константы расчёта:
![epsilon[0] = 0.8850000000e-11, epsilon[r] = 1.](https://files3.vunivere.ru/workbase/00/03/70/14/images/image027.jpg)
Определим неизвестное
(напряжение или заряд):
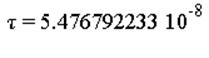
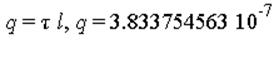
Определим ёмкость системы:
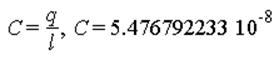
2. Построим графическую картину электростатического поля, соблюдая следующие требования:
а) разность потенциалов между двумя любыми соседними линиями равного потенциала должна быть одна и та же;
б) поток вектора напряжённости электростатического поля во всех силовых трубках должен быть одинаков ;
в) при построении картины поля на каждой линии равного потенциала указать значение потенциала; на силовых линиях должно быть указано их направление и ограниченное данной линией значение потока напряжённости поля, отсчитываемое от некоторой фиксированной линии, принятой за начальную.
Силовые линии можно
построить на основе окружностей, пересекающих ось Y. Их центры лежат на
оси Y и
имеют координаты 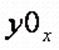 и имеют радиусы
и имеют радиусы 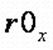 .
.
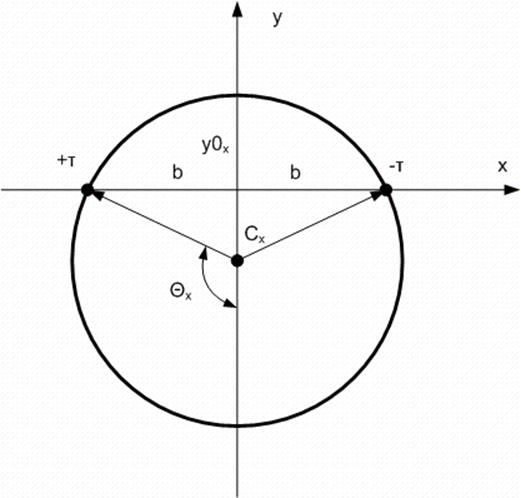
![y0[x] = b/tan(Theta[x])](https://files3.vunivere.ru/workbase/00/03/70/14/images/image034.jpg)
![r0[x] = b/sin(Theta[x])](https://files3.vunivere.ru/workbase/00/03/70/14/images/image035.jpg)
Зададимся шагом ![]() в π/6 и в соответствии с
этим вычислим радиусы и координаты центров окружностей в промежутке значений
угла [0,π].
Семейство данных окружностей и будет представлять собой картину силовых линий
для двух заряженных нитей.
в π/6 и в соответствии с
этим вычислим радиусы и координаты центров окружностей в промежутке значений
угла [0,π].
Семейство данных окружностей и будет представлять собой картину силовых линий
для двух заряженных нитей.
Определим аналитическое
выражение для потока через плоскую поверхность высотой y0, отсчитывая от оси х и длиной l, расположенную
перпендикулярно электрическим осям цилиндров. Ось Y принадлежит данной
плоскости:
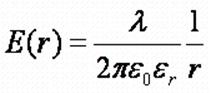 - напряжённость
поля, создаваемая бесконечной тонкой нитью, заряженной с линейной плотностью
заряда λ
на расстоянии r от
неё;
- напряжённость
поля, создаваемая бесконечной тонкой нитью, заряженной с линейной плотностью
заряда λ
на расстоянии r от
неё;
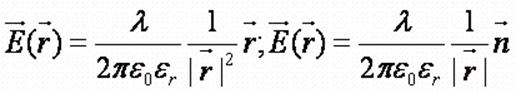 - то же в векторной форме (
- то же в векторной форме (![]() - радиус-вектор между
рассматриваемой точкой и осью нити/нитью;
- радиус-вектор между
рассматриваемой точкой и осью нити/нитью; ![]() - направляющий единичный вектор вектора
- направляющий единичный вектор вектора ![]() ).
).
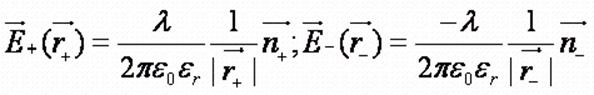 - векторы
напряжённостей полей создаваемых положительно и отрицательно заряженной нитью,
соответственно, имеющих одинаковые линейные плотности зарядов.
- векторы
напряжённостей полей создаваемых положительно и отрицательно заряженной нитью,
соответственно, имеющих одинаковые линейные плотности зарядов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.