Расчет электростатического поля несоосных параллельных цилиндров (Еr = 1; l = 7 м; U = 2000, D = 0,42 м), страница 2

Напряжённость в определённой точке пространства в нашем случае определяется, как суперпозиция двух этих напряжённостей в данной точке:
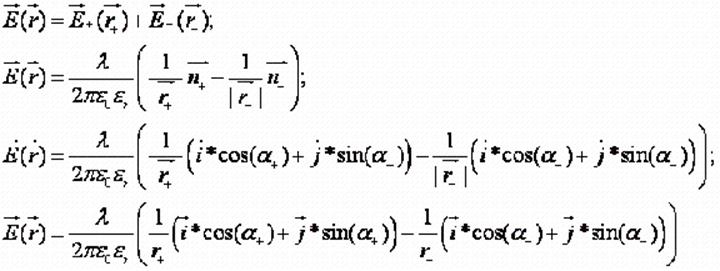(1)
α+ и α- - углы между радиус-векторами и вектором оси для положительно и отрицательно заряженной оси, соответственно.

Если выбираемые точки лежат на одной прямой, перпендикулярной отрезку, соединяющему нити, и делящей его пополам, то: 

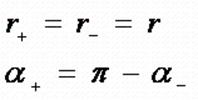
и конечное выражение для вектора напряжённости можно записать в форме:

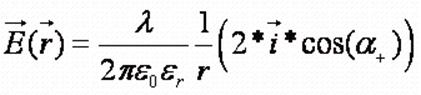
а так как направление вектора в данной точке детерминировано, то можно перейти к скаляру

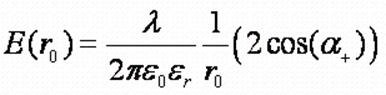
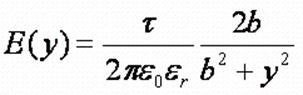- y - координата точки, отсчитываемая от одной из нитей (*).
E(y) - функция напряжённости электрического поля в точках данной поверхности.
Выражения потока примет следующий вид:

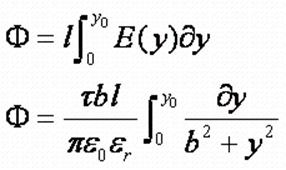
y для каждой силовой линии в 1 и 2-й четверти чертежа будет координатой пересечения соответствующей окружности и оси Y в положительной области.

y для каждой силовой линии в 3 и 4-й четверти чертежа будет координатой пересечения соответствующей окружности и оси Y в отрицательной области. 

 

Номер линии	1	2	3	4	5	6
Ф, В*м	18049.69191	14439.75353	10829.81515	7219.876764	3609.938377	0.

Θ, рад	1/6*Pi	1/3*Pi	1/2*Pi	2/3*Pi	5/6*Pi	Pi
Y, м	0.2779009792	0.9263365973e-1	0	-0.9263365973e-1	-0.2779009792	∞
R, м	0.3208924102	0.1852673194	0.1604462051	0.1852673194	0.3208924102	∞

Выражение потенциала в произвольной точке пространства записывается, как:
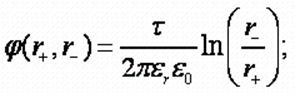, где
r- - расстояние от отрицательной электрической оси до точки;
r+ - расстояние от положительной электрической оси до точки;

Подставляя в эту формулу значения координат, получим:
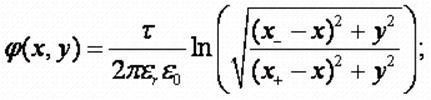, где
x- - координата отрицательно заряженной оси;
x+ - координата положительно заряженной оси;
x,y - координаты точки.
 

 

Построение эквипотенциальных поверхностей можно произвести на основе семейства окружностей. Радиусы и центры этих окружностей находятся из условий:
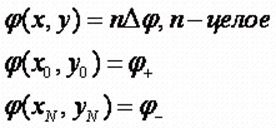, где
Δф - шаг следования эквипотенциальных поверхностей;
ф- - значение потенциала на поверхности отрицательно заряженного цилиндра;
ф+ - значение потенциала на поверхности положительно заряженного цилиндра.

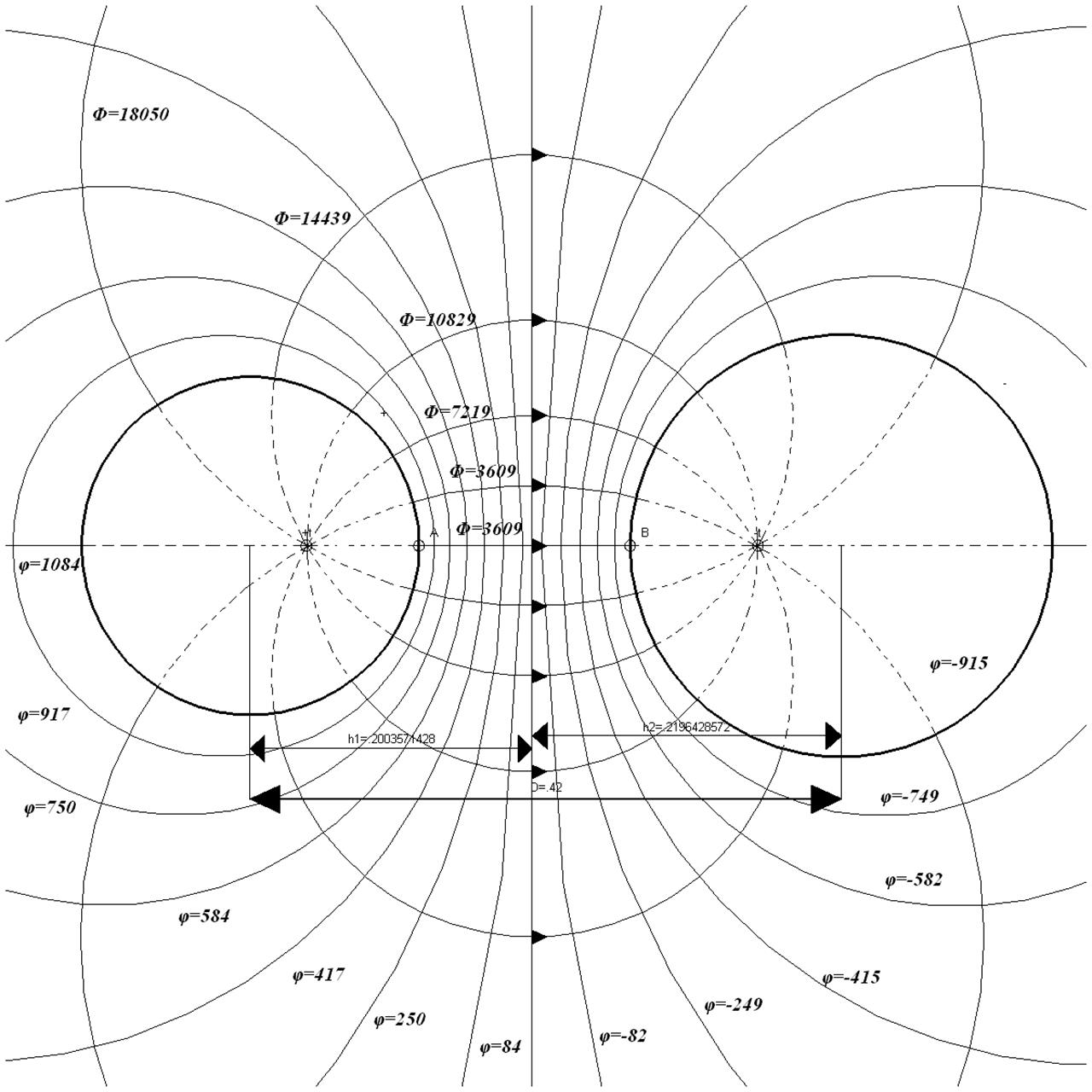
Учитывая следствия из теоремы Гаусса, построим чертёж, с нанесёнными силовыми линиями и эквипотенциальными поверхностями:
 

Х, м	R, м	ф, В
-0.2003571431 -0.2193836084 -0.2497248338 -0.3014858424 -0.4008446235 -0.6433766393 -1.880357181 1.921802819 0.6478943580 0.4024105440 0.3022410546 0.2501490641 0.2196428571	0.1200000004 0.1496201287 0.1913622426 0.2552464074 0.3673328565 0.6230493685 1.873499438 1.915093494 0.6277134015  0.3690410021 0.2561379908 0.1919155271 0.1499999998	1084.246054 917.5793870  750.9127202 584.2460535 417.5793867 250.9127201 84.24605342 -82.42061323 -249.0872799 -415.7539464 -582.4206131 -749.0872799 -915.7539466

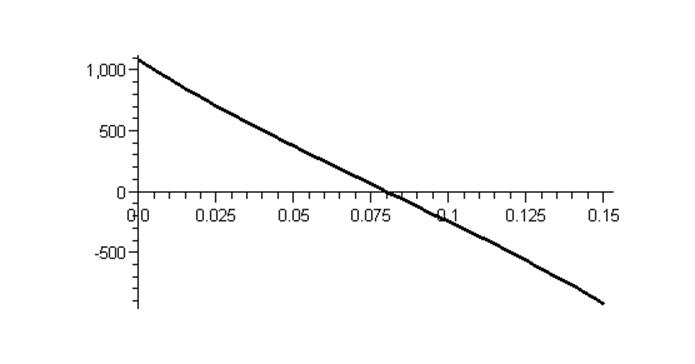
3. Вычислим и представим в виде графиков изменение потенциала и напряжённости элктростатического поля на линии, соединяющей наиболее близкие точки цилиндров, и распределение плотности заряда на поверхности цилиндра меньшего радиуса.

График изменения потенциала на линии A-B (функция ):
 

 

 

Аналитическую функцию для напряжённости поля найдём из следующих соображений (на линии A-B):

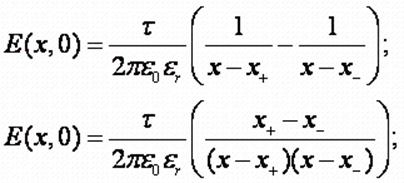
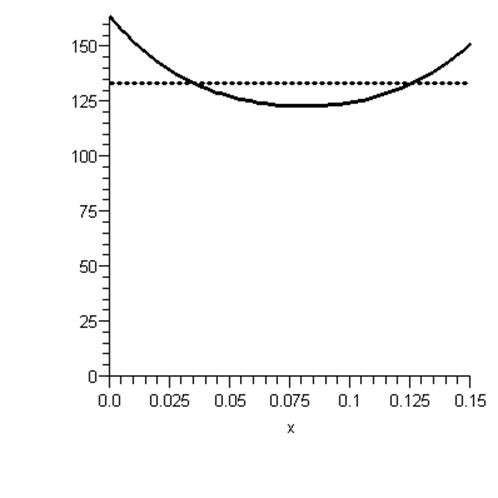
График напряжённости поля на отрезке A-B:
 

 

 

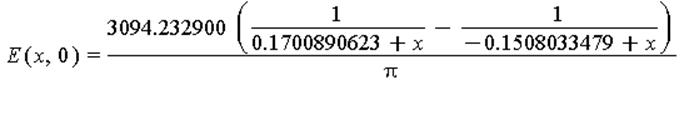
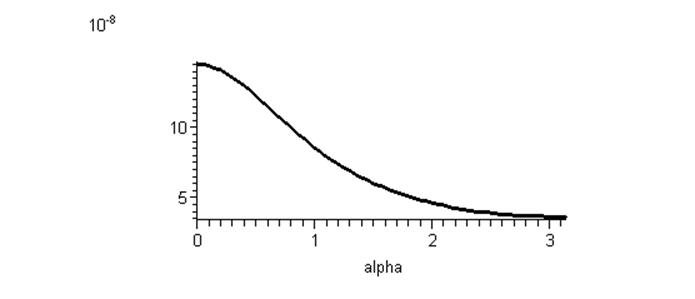
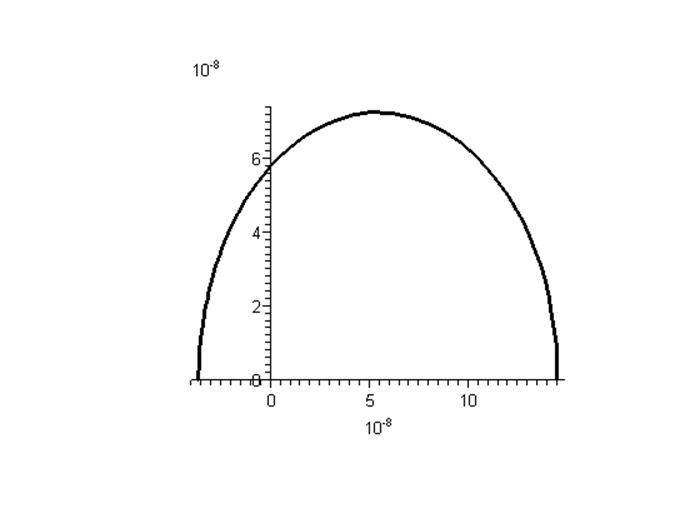
Построим зависимость плотности заряда на положительном цилиндре от угла поворота радиус-вектора, соединяющего точку на цилиндре и его геометрическую ось.
Вектор напряжённости поля, создаваемого двумя заряженными нитями: 

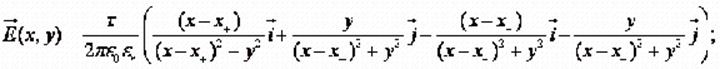
Координаты x,y определяются параметрическими выражениями:
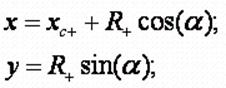, где

α - вышеуказанный угол;

R+ - радиус положительно заряженного цилиндра;

Xc+ - координата по оси X центра цилиндра.
 




 

 

 

 

 

 

 

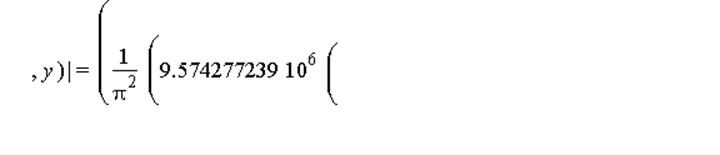
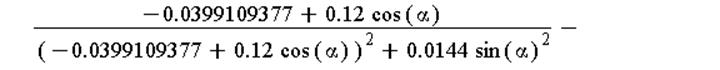
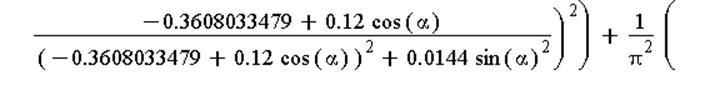
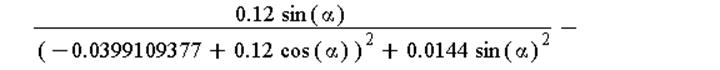
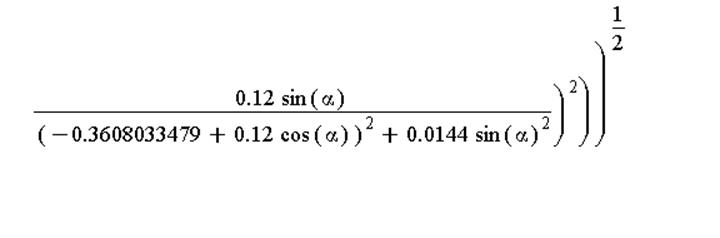
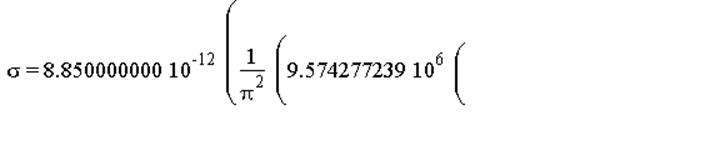
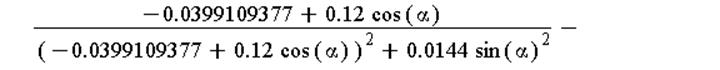
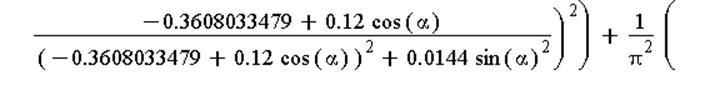
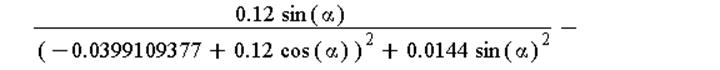
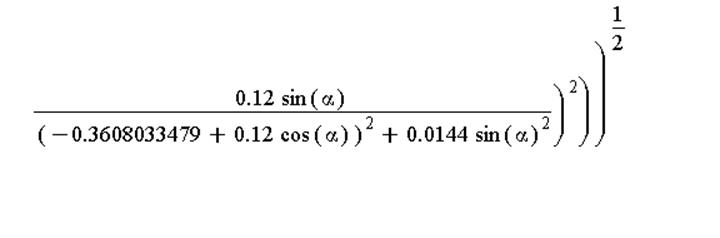
Построим зависимость в декартовых координатах:
 

 

Построим зависимость в полярных координатах: