






1. Представить сложный четырёхполюсник в виде двух простых и определить способ их соединения.
2. Определить коэффициенты матриц А элементарных четырёхполюсников, а также коэффициенты других матриц, соответствующих соединению четырёхполюсников.
3. Используя правила сложения и умножения матриц, определить коэффициенты матрицы А составного четырёхполюсника.
4. Определить собственные и рабочие параметры составного четырёхполюсника (Zc1, Zc2, g, a, b, Zвх1, Zвх2, aраб, aвн).
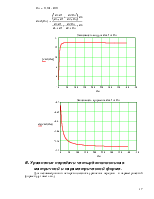
5. Рассчитать и построить зависимости модуля и аргумента входного сопротивления составного четырёхполюсника от сопротивления нагрузки Zвх1(Rн), Yвх1(Rн).
6. Записать уравнения передачи четырёхполюсников в матричной и параметрической формах.
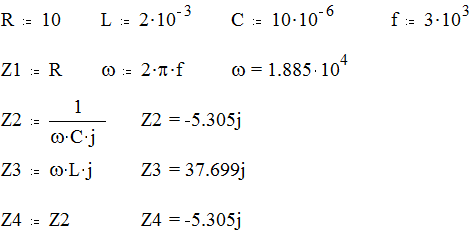
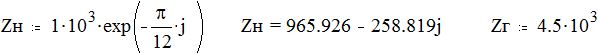
Определять коэффициенты четырёхполюсников целесообразно с помощью непосредственного применения законов Ома и Кирхгофа.
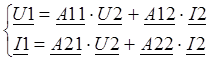
Запишем выражение первого закона Кирхгофа для узла а:
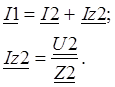
По второму закону Кирхгофа:
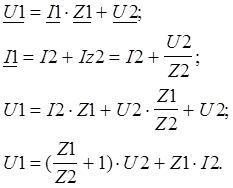
Отсюда (все вычисления производятся при помощи пакета Mathcad 6.0):
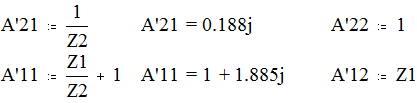
Произведём проверку правильности вычислений:
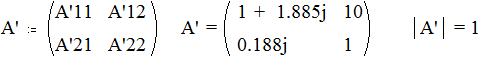
Проверка показала, что расчёт коэффициентов матрицы А произведён правильно.
Произведём аналогичный расчёт коэффициентов матрицы А для второго четырёхполюсника.

Коэффициенты других матриц, соответствующих данному соединению определим из таблицы 14.1 [1] с.427.
Для первого четырёхполюсника:
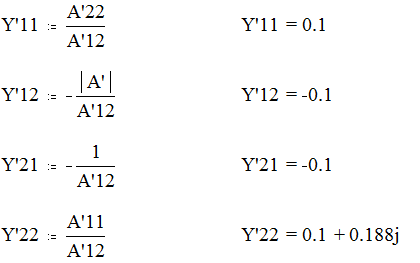
Для второго четырёхполюсника:
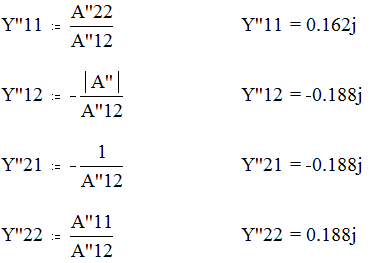
Для параллельного соединения четырёхполюсников справедливы соотношения:
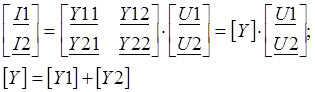
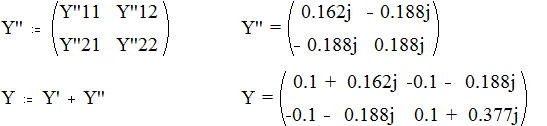
Зная коэффициенты матрицы Y можно определить коэффициенты матрицы А:

Произведём расчёт характеристических сопротивлений Zc1 и Zc2 со стороны входа и выхода, определяющих входные сопротивления четырёхполюсника в согласованном режиме.
Для этого предварительно определим сопротивления короткого замыкания и холостого хода со стороны входных и выходных зажимов четырёхполюсника Zxx1,Zxx2,Zкз1,Zкз2.
Zкз1 определяется при замкнутых зажимах 2-2’, Zxx1 – при разомкнутых.
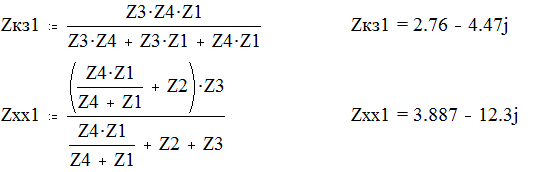
Zкз2 определяется при замкнутых зажимах 1-1’, Zxx2 – при разомкнутых.
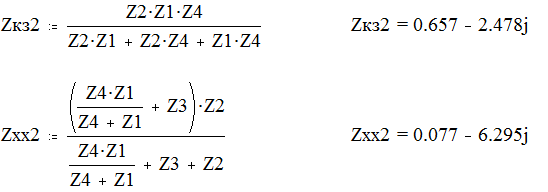
Отсюда определяем Zc1 и Zc2, g, a, b:

Определим входное сопротивление четырёхполюсника при подключенной нагрузке к зажимам 2-2’ Zвх1; к зажимам 1-1’ – Zвх2:
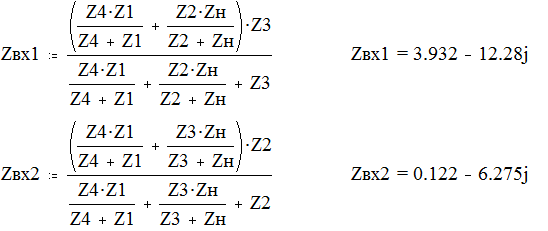
Определение рабочих параметров четырёхполюсника: aраб(рабочее затухание), авн(вносимое затухание). Для определения этих параметров необходимо предварительно определить:
а1 – дополнительное затухание, вызванное несогласованностью на входе;
а2 – дополнительное затухание, вызванное несогласованностью на выходе;
а3 – дополнительное затухание, вызванное взаимодействием отражений;
k1, k2 – коэффициенты отражения на входе и на выходе;
а4 – дополнительное затухание, вызванное несогласованностью сопротивлений генератора и нагрузки.

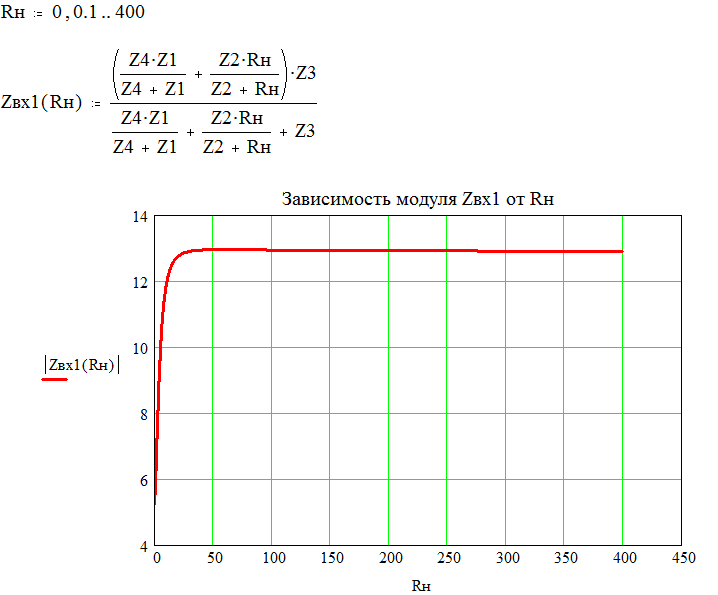
Для несимметричного четырёхполюсника уравнения передачи в параметрической форме будут иметь вид:
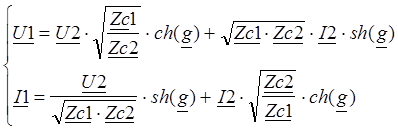
Расчёт коэффициентов перед U2 и I2 произведём при помощи пакета Mathcad:
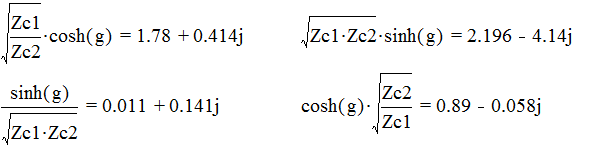
Тогда последняя система запишется в виде:
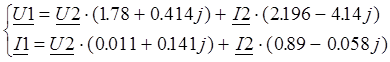
Уравнения передачи в матричной форме:
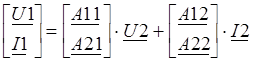

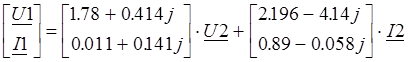
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.