Расчет цепочечных и полиноминальных фильтров

Республика Беларусь

Белорусский государственный

университет транспорта

Кафедра «Электротехника»

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №3 по курсу ТЛЭЦ

“ Расчет цепочечных и полиноминальных фильтров ”

шифр № 546

ВЫПОЛНИЛ:                                                                                                              ПРИНЯЛ:

студент группы  ЭМ-31                                                                                   ассистент

Муравьев С.В.                                                                  Грапов А.В.

г. Гомель 2004г.

Расчет цепочечных и полиноминальных фильтров.

Рассчитать электрический фильтр для работы между генератором и приёмником, имеющий заданную частотную характеристику затухания.

Исходные данные:

Дополнительное затухание в полосе пропускания

Минимальное затухание в полосе задержки на частоте  

Частоты среза  

Фиксированная частота в полосе задержки

Сопротивление нагрузки

Тип – фильтр Чебышева.

● Из-за несогласованности фильтра с нагрузкой возникает дополнительное затухание, поэтому расчётное значение  в ПЗ следует увеличить на величину 0.69 Нп:

● Определим частоты:

а) среднеквадратичную полосно-пропускающего фильтра:

б) граничную нижней полосы задержки: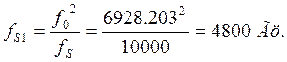

● Коэффициент преобразования ПП составляет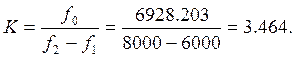

● Нормированная частота ФПНЧ:

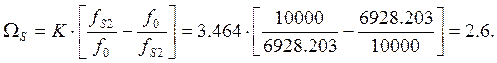
В качестве проверки:

● Далее найдём порядок ФПНЧ. Для этого воспользуемся следующей формулой:

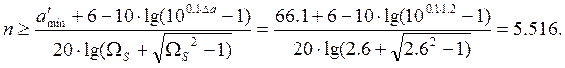
Т. к. округление необходимо проводить в сторону увеличения значения, примем n=6.

● Определим передаточную функцию в нормированных величинах.

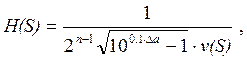 где  - полином Гурвица.

Вначале найдём вспомогательные постоянные для определения полюсов передаточной функции:

 

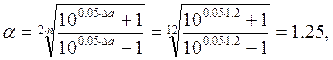
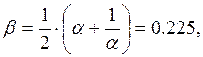
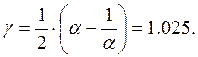
Первоначальное количество полюсов  Рассчитываем полюсы передаточной функции фильтра Чебышева по формуле: 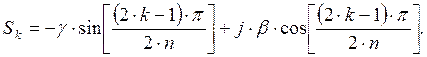 В результате расчёта получим:

Из этих 12-ти значений выбираем те, у которых действительная часть отрицательна, т.е. первые шесть ().  Полином Гурвица имеет вид:

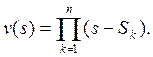
Полином Гурвица шестого порядка упрощается до многочлена шестой степени с коэффициентами:

     

Таким образом, полином Гурвица можно представить в следующем виде:

● Далее найдём функцию фильтрации.

1) Составим полином Чебышева 6-ого порядка (используя мат. справочник)

2) Получим выражение нормированного значения полинома Чебышева:

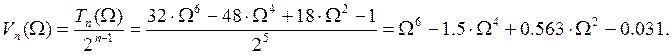
3) В последнем выражении заменим  на переменную ; при этом все его члены считаются положительными независимо от их знака:

Входное сопротивление ФПНЧ в нормированных величинах:

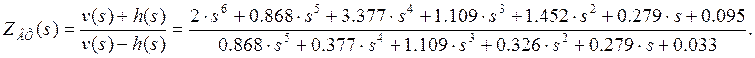
Разложив данную дробь в цепную, получим (разложение приведено ниже):

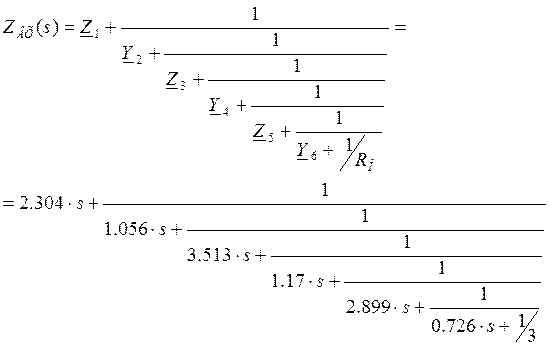
Отсюда нормированные значения элементов ФПНЧ:

     

 

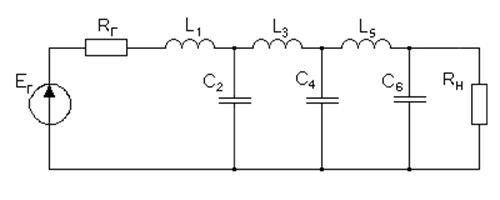
Схема ФПНЧ с нормированными элементами:

Перейдём от ФПНЧ к ППФ в нормированном виде.

 

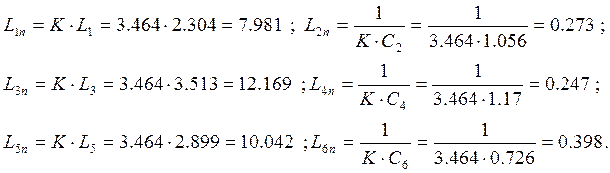
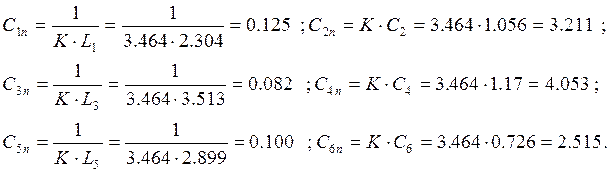
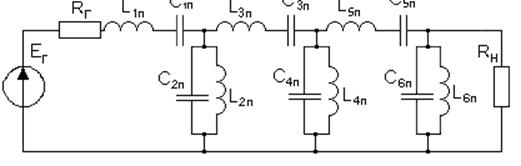
Схема полосопропускающего фильтра

Коэффициенты денормирования элементов:

1)  для индуктивности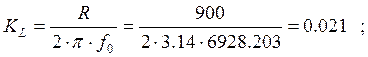

2)  для ёмкости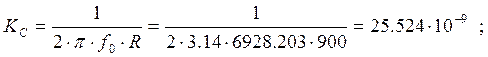

3)  для нагрузки

Принципиальная схема фильтра:

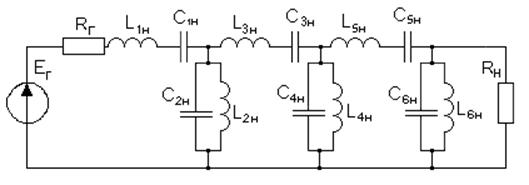
Определим номинальные значения элементов по формулам:   Результаты данного расчёта сведены в таблицу:

значение	165.012	5.652	251.6	5.101	207.626	8.221

значение	3.198	93.371	2.097	103.451	2.542	64.192

Произведём расчёт ослабления фильтра и построим характеристику затухания.

 где  - полином Чебышева,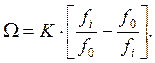  

Возьмём в качестве текущей частоты несколько значений и сведём результаты в таблицу

		6000 8000		10000   4800		12000   4000
	0	-1	1	2.6	-2.6		4	-4
	0	1.2		72.884		96.544

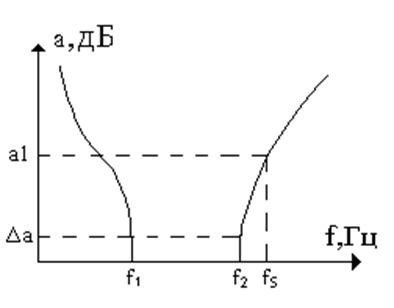
Частотная характеристика затухания:

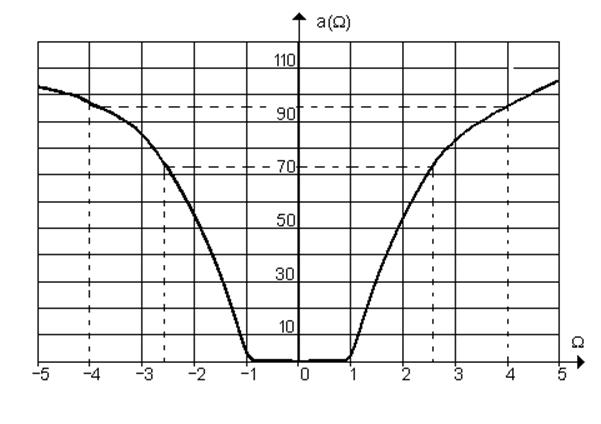
2s6+0.868s5+3.377s4+1.109s3+1.452s2+0.279s+0.095	0.868s5+0.377s4+1.109s3+0.326s2+0.279s+0.033
2s6+0.868s5+2.555s4+0.751s3+0.623s2+0.76s	2.304s       (z1)
0.822s4+0.358s3+0.829s2+0.203s+0.095

0.868s5+0.377s4+1.109s3+0.326s2+0.279s+0.033	0.822s4+0.358s3+0.829s2+0.203s+0.095
0.868s5+0.377s4+0.875s3+0.214s2+0.1s	1.056s       (y2)
0.234s3+0.112s2+0.179s+0.033

0.822s4+0.358s3+0.829s2+0.203s+0.095	0.234s3+0.112s2+0.179s+0.033
0.822s4+0.358s3+0.629s2+0.116s	3.513s       (z3)
0.2s2 + 0.087s+0.095

0.234s3+0.112s2+0.179s+0.033	0.2s2+0.087s+0.095
0.234s3+0.112s2+0.111s	1.17s       (y4)
0.069s+0.033

0.2s2+0.087s+0.095	0.069s+0.033
0.2s2+0.087s	2.889s       (z5)
0.095

0.069s+0.033	0.095
0.069s	0.726s       (y4)
0.033

0.095	0.033
0.095	3               (r)
0

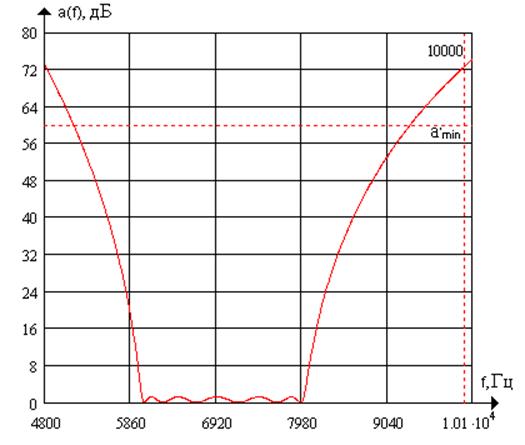
Общий вид частотной характеристики затухания:

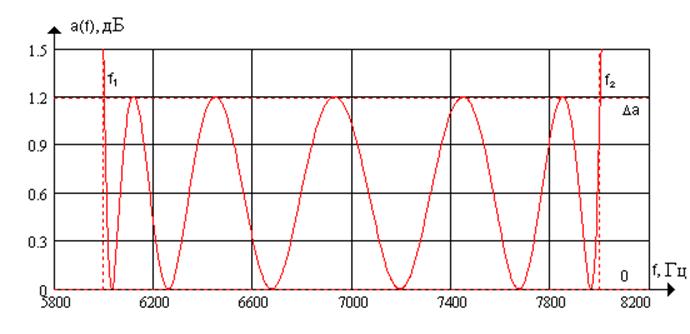
Полоса задержки фильтра: