Для заданной схемы четырехполюсника требуется:
1. Представить сложный четырехполюсник в виде двух простых и определить способ их соединения.
2. Определить коэффициенты матрицы А элементарных четырехполюсников, а также коэффициенты других матриц, соответствующих соединению четырехполюсника.
3. Используя правила сложения и умножения матриц, определить коэффициенты матрицы А составного четырехполюсника.
4. Определить собственные и рабочие параметры составного четырехполюсника (![]() ).
).
5. Рассчитать и построить зависимости модуля и аргумента входного сопротивления
составного четырехполюсника от сопротивления нагрузки ![]() .
.
6. Записать уравнения передачи четырехполюсника в матричной и параметрической формах.
Схема исходного четырехполюсника:
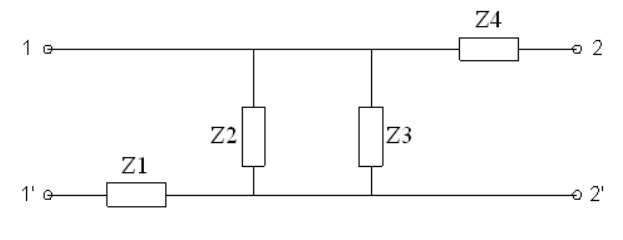
Исходные данные:
Таблица 1
|
Значения L, C, R |
С=10мкФ |
L=2 мГн |
R=10 Ом |
|
|
|
|
|
|
L |
R |
C |
L |
Таблица 2
|
Генератор |
Нагрузка |
f, кГц |
||
|
Модуль (ZГ, кОм) |
угол |
Модуль (Zн, кОм) |
угол |
|
|
12 |
-10˚ |
2,8 |
-10˚ |
2 |
Решение:
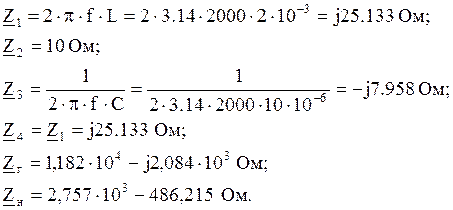
1 Представление сложного четырехполюсника в виде двух простых и определение способа их соединения
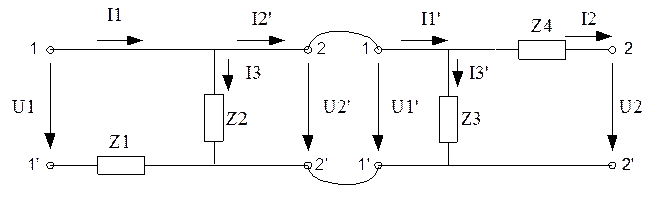
Тип соединения – каскадное (два Г-образных двухполюсника).
Определять коэффициенты четырехполюсников целесообразно с помощью непосредственного применения законов Ома и Кирхгофа.
Рассмотрим первый четырехполюсник.
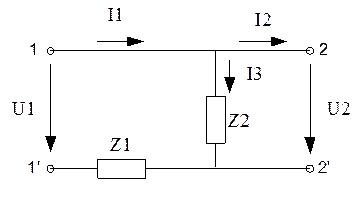
Основное уравнение передачи для этого четырехполюсника будет иметь вид:
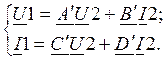
Рассмотрим режим холостого хода (I`2=0);
![]() ;
;
Отсюда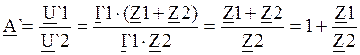 .
.
Т.е. 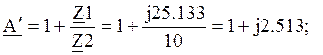
![]()
Отсюда 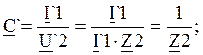
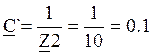 Cм;
Cм;
Рассмотрим режим короткого замыкания (![]() =0):
=0):
![]()
Отсюда: 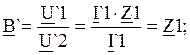
![]() ;
;
![]() ;
;
Отсюда: 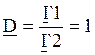 ;
;
Т.о. матрица ![]() ,будет
иметь вид:
,будет
иметь вид: 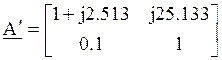 .
.
Определитель этой матрицы: |А`|=1.
Рассмотрим второй четырехполюсник.
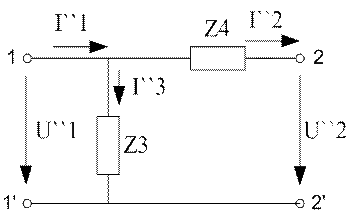
Основное уравнение передачи для этого четырехполюсника будут иметь вид:
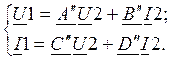
Рассмотрим режим холостого хода (I`2=0);
![]() ;
;
Отсюда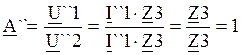 .
.
![]()
Отсюда 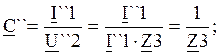
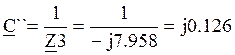 Cм;
Cм;
Рассмотрим режим короткого замыкания (![]() =0):
=0):
![]()
Отсюда: 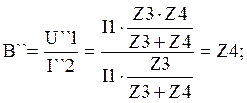
![]() ;
;
![]() ;
;
Отсюда: 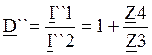 ;
;
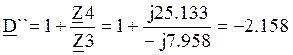
Т.е. матрица 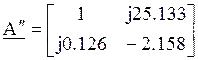 .
.
Определитель этой матрицы: |А``|=1.
3 Определение коэффициентов матрицы А составного четырехполюсника
Т.к. у нас каскадное соединение, то матрица А составного четырехполюсника равна произведению матриц простых четырехполюсников.
Т.е.
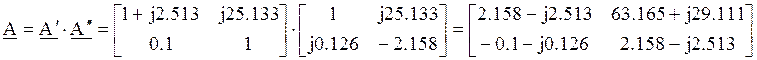
![]()
Следовательно коэффициенты матрицы А имеют вид:
![]()
![]()
![]()
![]()
Произведем расчет характеристических сопротивлений![]() со стороны входа и выхода, определяющих
входные сопротивления четырехполюсника в согласованном режиме.
со стороны входа и выхода, определяющих
входные сопротивления четырехполюсника в согласованном режиме.
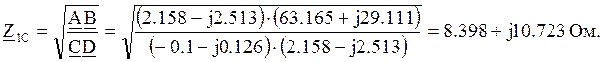
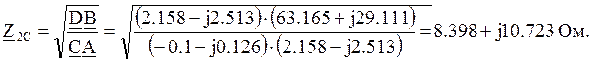
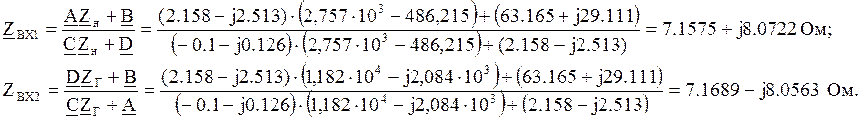
Определим
характеристическую постоянную затухания четырехполюсника ![]() , где
, где ![]() –
характеристический коэффициент затухания, а
–
характеристический коэффициент затухания, а ![]() –
характеристический коэффициент фазы четырехполюсника.
–
характеристический коэффициент фазы четырехполюсника.
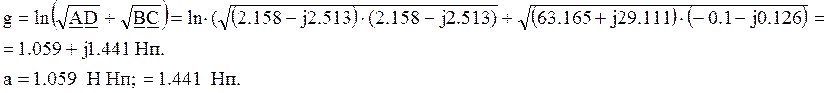
Определение
рабочих параметров четырехполюсника: ![]() (рабочее
затухание) и
(рабочее
затухание) и ![]() (вносимое затухание). Для
определения этих параметров необходимо предварительно определить:
(вносимое затухание). Для
определения этих параметров необходимо предварительно определить:
![]() – дополнительное затухание, вызванное
несогласованием на входе;
– дополнительное затухание, вызванное
несогласованием на входе;
![]() – дополнительное затухание,
вызванное несогласованием на выходе;
– дополнительное затухание,
вызванное несогласованием на выходе;
![]() – дополнительное затухание,
вызванное взаимодействием отражений;
– дополнительное затухание,
вызванное взаимодействием отражений;
![]() – коэффициенты отражения на входе и выходе;
– коэффициенты отражения на входе и выходе;
![]() – дополнительное затухание,
вызванное несогласованностью сопротивлений генератора и нагрузки.
– дополнительное затухание,
вызванное несогласованностью сопротивлений генератора и нагрузки.
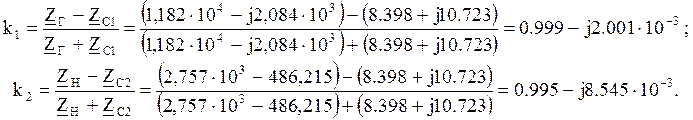
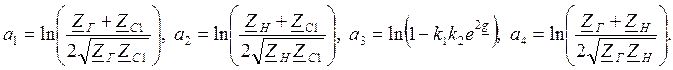
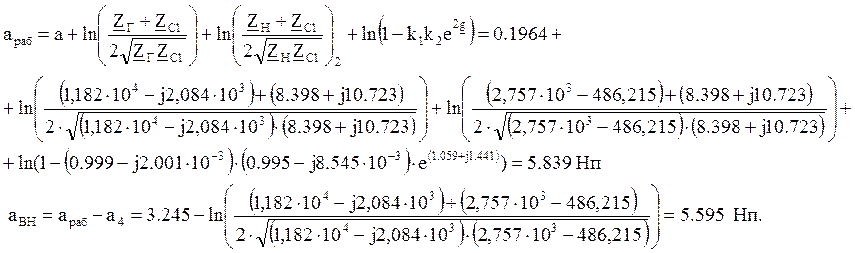
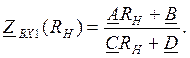
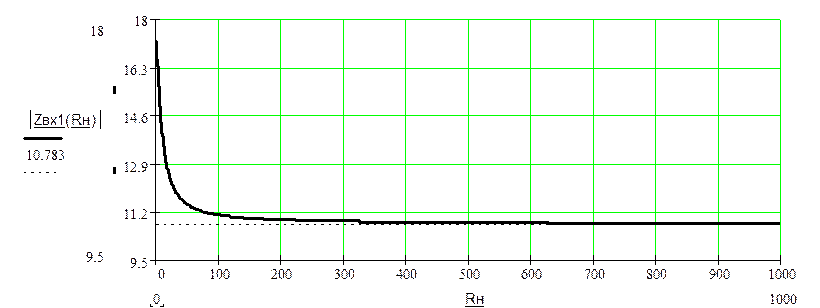
Зависимость модуля ![]() от RН.
от RН.
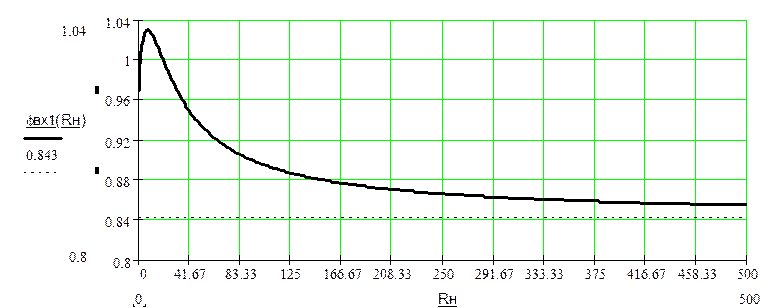
Зависимость аргумента фвх1 от RН
6 Уравнения передачи четырехполюсника в матричной и параметрической форме
Для несимметричного четырехполюсника уравнения передачи в параметрической форме будут иметь вид:
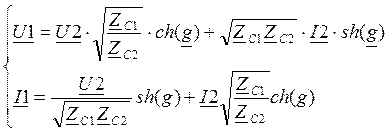
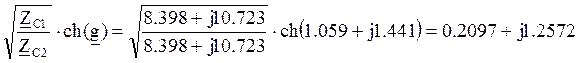 ;
;
![]()
![]() ;
;
![]()
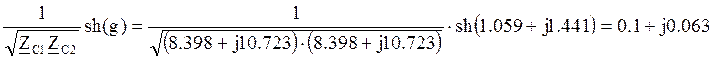 ;
;
![]()
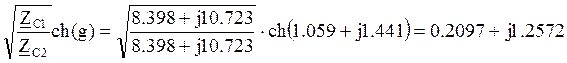 .
.
Тогда система примет следующий вид:
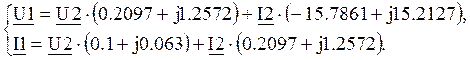
Уравнения передачи в матричной форме:
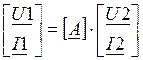 ;
;
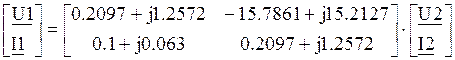 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.