
Задача №8.19
Условие: Вероятность попадания мячом в корзину при каждом броске для данного баскетболиста равна 0.4. Случайная величина X – число попаданий в серии из четырёх бросков M[X]=1.6; D[X]=0.96.
Решение:
Вычислим по формуле Бернули возможные значения данной случайной величины:
0
P(X=0) = C4*(0.4)0*(0.6)4=0.1296;
1
P(X=1) = C4*(0.4)1*(0.6)3=0.3456;
2
P(X=2) = C4*(0.4)2*(0.6)2=0.3456;
3
P(X=3) = C4*(0.4)3*(0.6)1=0.1536;
4
P(X=4) = C4*(0.4)4*(0.6)0=0.0256;
Проверка: P0 + P1 + P2 + P3 + P4 = 0.1296 + 0.3456 + 0.3456 + 0.1536 + 0.0256 = 1;
Ряд распределения случайной величины:
|
Xi |
0 |
1 |
2 |
3 |
4 |
|
Pi |
0.1296 |
0.3456 |
0.3456 |
0.1536 |
0.0256 |
|
|
|
|
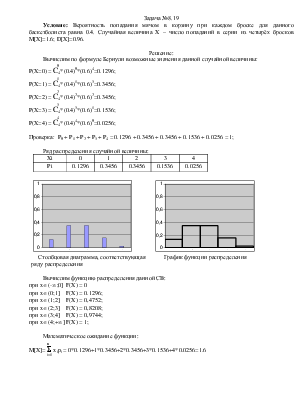
Столбцовая диаграмма, соответствующая ряду распределения |
График функции распределения |
Вычислим функцию распределения данной СВ:
при xÎ (-¥;0] F(X) = 0
при xÎ (0;1] F(X) = 0.1296;
при xÎ (1;2] F(X) = 0,4752;
при xÎ (2;3] F(X) = 0,8208;
при xÎ (3;4] F(X) = 0,9744;
при xÎ (4;+¥] F(X) = 1;
Математическое ожидание функции:
n
M[X]= S xipi = 0*0.1296+1*0.3456+2*0.3456+3*0.1536+4*0.0256=1.6
i=1
Данная случайная величина имеет две моды: xmod=2, xmod=3, т.е. наиболее вероятное число попаданий в корзину равно 2 и 3.
Вычислим дисперсию:
n
D[X]= S xi2pi – (M[X])2 = 0*0.1296+1*0.3456+4*0.345+9*0.1536+16*0.0256 -1.62=0.96
i=1
Среднее квадратичное отклонение:
s[X]= (D[X])-1 = 0.9798
Т.е. среднее квадратичное отклонение числа мячей, которые попадут в корзину, равно 0.9798
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.