Использование конкретного способа может зависить от наличия определённой компонентной базы. Например первый способ предпочтительней при синтезе устройства на базе ПЛИС, или ПЛМ и последующей реализации.
Преобразование кода:двоично-десятичный – (2 из 5);
Базис реализации: И-НЕ.
Используемые формулы:
![]() (Правило де Моргана)
(Правило де Моргана)
Определим таблицу соответствия между кодом 8421, кодом (2 из 5), а также десятичными цифрами.
Таблица 9 - Соответствие между кодами.
|
Десятичная цифра |
Двоичный код (8421) |
Двоичный код (2 из 5) |
|
0 |
0000 |
11000 |
|
1 |
0001 |
01100 |
|
2 |
0010 |
00110 |
|
3 |
0011 |
00011 |
|
4 |
0100 |
10001 |
|
5 |
0101 |
10100 |
|
6 |
0110 |
01010 |
|
7 |
0111 |
00101 |
|
8 |
1000 |
10010 |
|
9 |
1001 |
01001 |
Преобразователь кодов должен правильно обработать двоично-десятичный код (под каждый десятичный разряд в коде 2 из 5 должна быть выделена своя независимая область в выходном коде, вследствие чего преобразователь кода будет состоять из 2-х частей – кодирование единиц и кодирование десятков).
Составим таблицу истинности блока-преобразователя единиц.
Таблица 10 - Соответствие между кодами.
|
Десятичная цифра |
Двоичный код (8421) |
Двоичный код (2 из 5) |
|||||||
|
I1 |
I2 |
I3 |
I4 |
Y1 |
Y2 |
Y3 |
Y4 |
Y5 |
|
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
|
2 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
|
3 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
|
4 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
5 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
|
6 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
|
7 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
|
8 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
9 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
Зададим функции выходов единиц Y1-Y5 картами Карно и произведём их минимизацию для ДНФ.
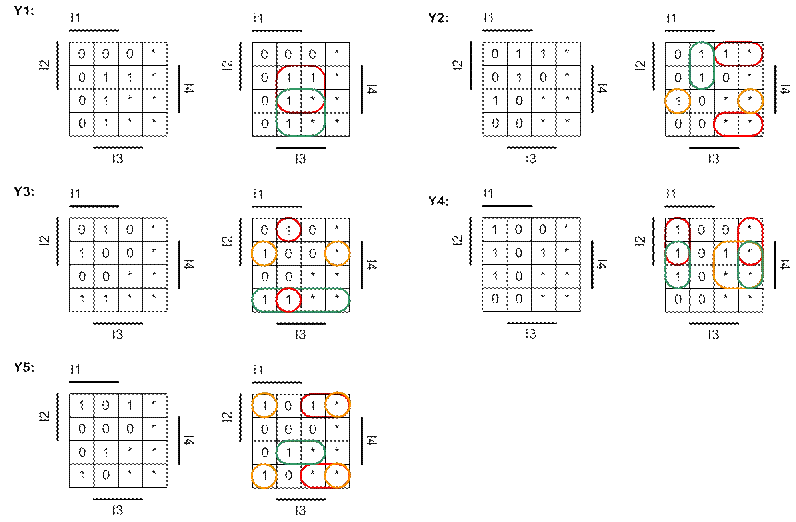 Рисунок 23 -
Минимизация функций картами Карно.
Рисунок 23 -
Минимизация функций картами Карно.
Составим минимизированные выражения для функций Y1-Y5:
![]()
![]()
![]()
![]()
![]()
Преобразуем эти выражения следующим образом с помощью правила де Моргана:
![]()
![]()
![]()
![]()
![]()
Реализуем блок-преобразователь в абстрактных логических элементах.
|
Рисунок 24 - Блок-преобразователь единиц (абстрактные элементы). |
Составим таблицу истинности блока-преобразователя десятков.
Таблица 11 - Соответствие между кодами.
|
Десятичная цифра |
Двоичный код (8421) |
Двоичный код (2 из 5) |
||||
|
I5 |
Y6 |
Y7 |
Y8 |
Y9 |
Y10 |
|
|
0 |
0 |
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
0 |
1 |
1 |
0 |
0 |
В данном случае из-за простоты получаемых выражений не будем проводить минимизацию. Составим минимизированные выражения для функций Y6-Y10:
![]()
![]()
![]()
![]()
![]()
Реализуем блок-преобразователь в абстрактных логических элементах.
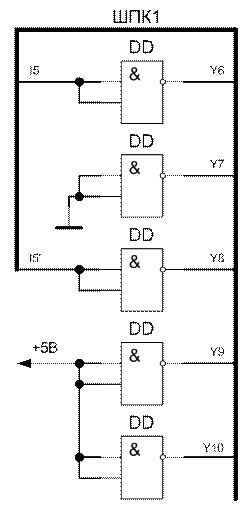
Рисунок 25 - Блок-преобразователь десятков (абстрактные элементы).
Логически избыточные элементы на выходах разрядов десятков необходимы для согласования входных/выходных напряжений, токов и сопротивлений, а также для регенерации поступающего сигнала.
Объединим все схемы в схему законченного функционального устройства в абстрактных элементах.
|
Рисунок 26 - Заданный преобразователь кода (абстрактные элементы). |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.