Разработка дискретного устройства (вид счётчика - суммирующий, базис реализации - И-НЕ, коэффициент счёта счётчика - 17), страница 4

-с последовательно-параллельным переносом (в счетчике выделяются блоки с параллельным переносом, связываемые последовательными связями).

Применение счетчиков с определенным типом счета обусловлено его функциональной задачей в более сложном устройстве.

Положительным свойством счетчиков с последовательным переносом является простота их построения, недостаток – достаточно большое время установления кода на выходе. Счетчики с параллельным переносом более сложны по структуре по сравнению со счётчиками с последовательным переносом, но они являются более быстродействующими. Счетчики с последовательно параллельным переносом применяются обычно тогда, когда имеются готовые ИМС счетчиков с параллельным переносом при наличии требования к минимуму количества микросхем на печатной плате.

Вид счётчика: суммирующий;

Базис реализации: И-НЕ;

Коэффициент счёта счётчика: 17;

Способ переноса счётчика: параллельно-последовательный;

Тип элемента памяти: Delay-триггер;

Используемые формулы:

 (Правило де Моргана)

, где

N – количество триггеров, необходимых для построения счётчика;

К_сч – коэффициент счёта счётчика.

Для построения параллельно-последовательного счётчика используем следующее разделение счётчика на составляющие (т.к. коэффициент счёта равен 17=1*10¹+7*10⁰ , то логично будет использовать двоично-десятичную систему счёта):

-единицы и десятки подсчитываются отдельными параллельными блоками-счётчиками;

-перенос из единиц в десятки осуществляется последовательным способом;

-т.к. коэффициент счёта у блока-счётчика единиц равен К_сч=10, то количество задействованных триггеров будет равно ;

-т.к. коэффициент счёта у блока-счётчика десятков равен К_сч=2, то количество задействованных триггеров будет равно ;

Определим таблицу переходов Delay-триггера. Построение счётчика будем производить на основе Delay-триггеров с прямым динамическим входом. Delay-триггеры с прямым динамическим синхронизирующим входом повторяют своё состояние на D-входе в момент изменения состояния на C►-входе с низкого на высокое.

Таблица 2 - Переходы Delay-триггера.

Определим таблицу истинности блока-счётчика единиц (К_сч=10).

Таблица 3 - Таблица истинности счётчика с К_сч=10 на Delay-триггерах.

Зададим возбуждающие функции входов D1-D4 картами Карно и произведём их минимизацию для ДНФ.

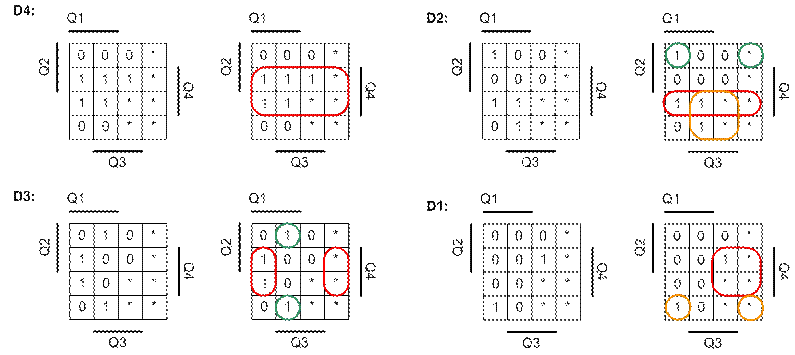
Рисунок 14 - Минимизация функций картами Карно.