Разработка амплитудно-выравнивающего корректора, страница 7

                                             l(t)

                                         S_c(l,t)                                                                                           t

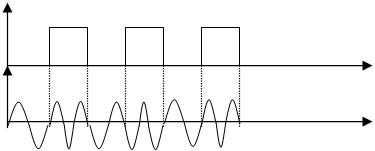
                                                 0       1       0      1       0        1

                                                                                                                                      t

Рис.3. 1.Диаграмма сигналов при ЧМ.

Выражение для напряжения вспомогательной частоты преобразования (несущей) в общем случае имеет вид   

u = U₀ cos(wt + y).

Мгновенные значения ординат кривой сигнала определяются выражением

u = U_W cos Wt.

В случае ЧМ частота w должна изменятся в соответствии с изменением мгновенных значений кривой сигнала

w(t) = w₀ + Dw cosWt.                  (1)

Здесь величина Dw представляет собой значение максимального отклонения от среднего ее значения w₀; эта величина называется девиацией частоты.

Зависимость между фазой и круговой частотой можно представить равенством

j(t) = w(t)dt.

Тогда изменение фазового угла при изменении частоты колебаний в соответствии с выражением (1) можно записать в виде

j(t) = (w₀ + Dw cosW t)dt = w₀t + t + C.

Считая, что постоянная интегрирования С представляет собой начальную фазу процесса (примем равной нулю), получим характерное для ЧМ выражение

u = U₀ cos(w₀t + sinWt) = U₀ cos(w₀t + M sinWt).               (2)

Величина М= называется индексом модуляции.

Выражение (2) показывает временную зависимость процесса ЧМ. Для получения спектральной  характеристики  ЧМ  колебаний  воспользуемся  соотношением     cos(x+y)=cosx cosy + sinx siny. Тогда выражение (2) можно представить как

u = U₀ [cos w₀t cos (M sin Wt) – sin w₀t sin (M sin Wt)].               (3)

Если М<<1, то принимая с некоторым приближением, что sin (M sin Wt)  M sin Wt и cos M sin Wt1, получим

u = U₀ [cos w₀t - M sin Wt sin w₀t ] = U₀ cos w₀t + MU₀/2 cos (w₀ + W)t –

                                              - MU₀/2 cos (w₀ - W)t.                                               (4)

Выражение (4) показывает, что в результате ЧМ появляются две боковые частоты (). Следует заметить, что выражение для одной из боковых частот имеет знак “минус”, что соответствует повороту вектора по фазе на 180⁰.

Определим спектр ЧМ колебаний без ограничения индекса модумяции М.. В выражении (3) величины cos (M sin Wt) и sin (M sin Wt) можно представить в виде рядов :

cos (M sin Wt) = J₀ (M) + 2 J_q(M) cos qWt

                                                     sin (M sin Wt) = 2 J_q(M) sin qWt            (5)

В этой формуле J_q(M) – коэффициенты ряда разложения функций, стоящих слева, на четные и нечетные составляющие. Эти коэффициенты являются функциями Бесселя первого рода q-порядка от аргумента М.

Для простейшего случая, когда сигнал является гармрническим колебанием с частотой W, приведенные соотношения позволяют представить формулу (3) так:

u = U₀ cos w₀t [ J₀ (M) + 2 J_q(M) cos qWt ] – U₀ sin w₀t [ 2 J_q(M) sin qWt ]=

= U₀ J₀ (M) cos w₀t +  2U₀ J_q(M) cos w₀t cos qWt - 2U₀ J_q(M) sin w₀t sin qWt.

Пользуясь известными из тригонометрии формулами

cosx cosy = ½ cos (x+y) + ½ cos (x-y);

sinx siny = ½ cos (x-y) + ½ cos (x+y),

можно определить частотные составляющие полученного спектра

u = U₀ J₀ (M) cos w₀t +   U₀ J_q(M) cos (w₀ + qW)t +(-1)^q U₀ J_q(M) cos (w₀ -qW)t.   (6)

Таким образом, даже при модуляции только одной частотой появляются две боковые полосы, содержащие комбинационные составляющих как от четных, так и от нечетных гармоник частоты W. Из выражения (6) следует, что разные знаки появляются только у боковых частот соответствующих нечетным гармоникам частоты сигнала. С увеличением коэффициента М= относительно возрастают также и амплитуды высших гармоник, а следовательно, и полоса частот, занимаемая преобразованным спектром.