Применение методов регрессионного анализа для аппроксимации вольтамперных характеристик диодов

Регрессионный анализ

Аппроксимация нелинейных характеристик элементов технических систем

методами линейного и нелинейного регрессионного анализа

Очень часто в реальных инженерных задачах характеристики элементов заданы в виде таблиц расчетных и/или экспериментальных данных.

В этом случае для моделирования систем требуется заменить наборы табличных данных аналитическими зависимостями. При этом экспериментальные данные, как правило, зашумлены помехами, соответственно, их необходимо фильтровать и далее применять алгоритмы поиска аппроксимирующих кривых. Если удается найти решение в полиномиальном базисе, то в этом случае достаточно использовать методы и алгоритмы линейной регрессии. В ряде случаев использование полиномов в силу особенностей их поведения при возрастании степени не приемлемо. В таких случаях можно пытаться применить методы нелинейной регрессии, которые позволяют находить аппроксимирующие зависимости в сложных нелинейных базисах.

Рассмотрим применение методов регрессионного анализа для аппроксимации вольтамперных характеристик диодов.

> restart: 

>   with (stats) : with (plots):  with ( stats [statplots] ) :

Warning, the name changecoords has been redefined

Итак, пусть вольтамперная характеристика задана набором табличных данных:

> Ud := [0, 0.2, 0.4, 0.6, 0.8 , 1] :

> Id := [0.0, 0.15, 0.58, 1.67, 4.82, 15.5] :

В начале найдем интерполирующий полином для приведенного набора данных, построим его график, предварительно записав его в переменную g1:

> f := interp (Ud, Id, z) ;

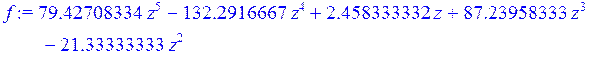
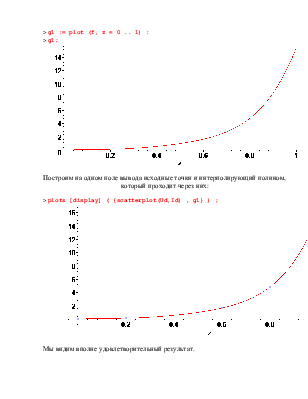
> g1 := plot (f, z = 0 .. 1) :

> g1;

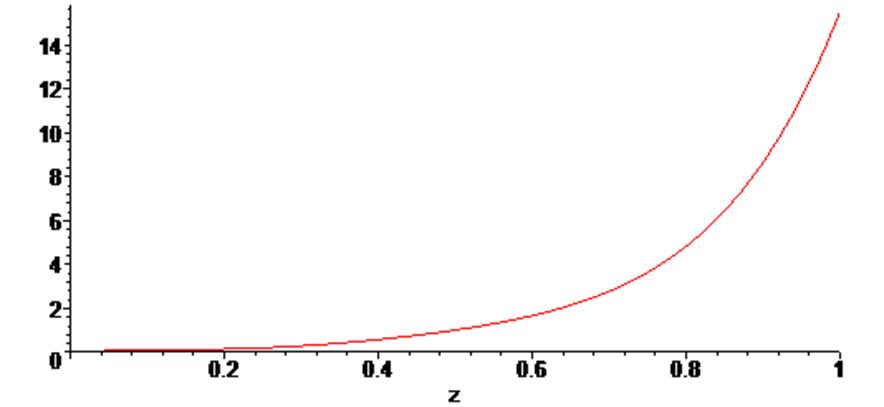
Построим на одном поле вывода исходные точки и интерполирующий полином, который проходит через них:

> plots [display] ( {scatterplot(Ud,Id) , g1} ) ;

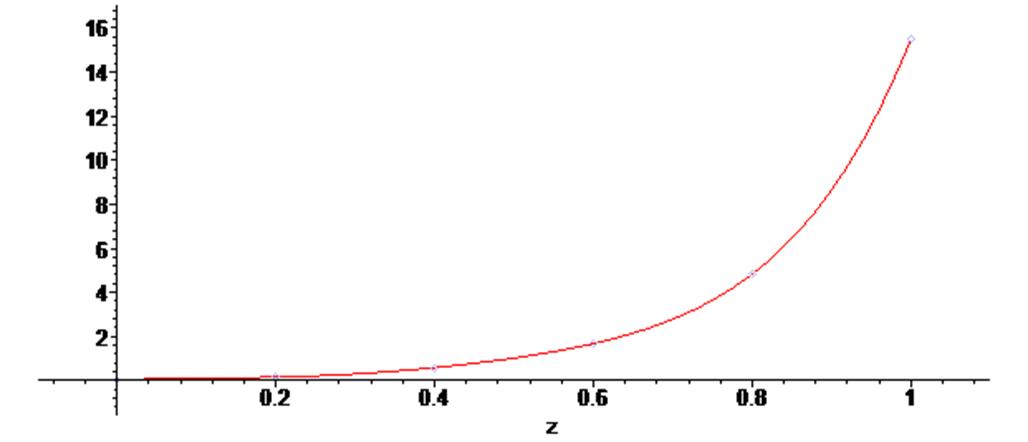
Мы видим вполне удовлетворительный результат.

Тем не менее для этого же набора данных найдем аппроксимирующую кривую в виде

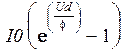
так как именно в таком виде как правило приводятся аналитические характеристики полупроводниковых элементов.

Для этого применим библиотеку Statistics , так как в неё включены функции Fit и  NonlinearFit , выполняющие поиск сложных аналитических  зависимостей по табличным данным, т.е. реализующие алгоритмы  регрессии.

Следует обратить внимание на то обстоятельство, что функция Fit этой же библиотеки выполняет как линейную, так и нелинейную регрессию в зависимости от задаваемых параметров, т.е. имеет универсальный  характер.

ФункцияNonlinearFit ориентирована на выполнение нелинейного регрессионного анализа.

> restart:

> with (plots):  with ( stats [statplots] ) : with(Statistics):

Warning, the name changecoords has been redefined

Вольт-амперную характеристику запишем в массивы X  и Y:

> X := [0, 0.2, 0.4, 0.6, 0.8 , 1]:

Y := [0.0, 0.15, 0.58, 1.67, 4.82, 15.5]:

Итак, найдём параметры аппроксимирующей функции  вида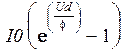 

в которой аргументом является переменная Ud.

Воспользуемся последовательно функциями Fit и  NonlinearFit  и затем сравним результаты

> F := Fit(I0 * ( exp (Ud/phi) - 1 ), X, Y, Ud);

> FF := NonlinearFit(I0 * ( exp (Ud/phi) - 1 ), X, Y, Ud);

Как видим, результат работы функций одинаков.

 Построим график аппроксимирующей кривой, а затем построим на одном поле вывода исходные точки и аппроксимирующую функцию:

> G := plot (F, Ud = 0 .. 1 ) :

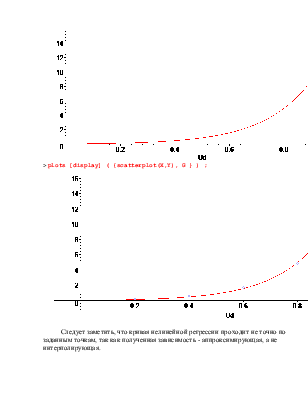
> G;

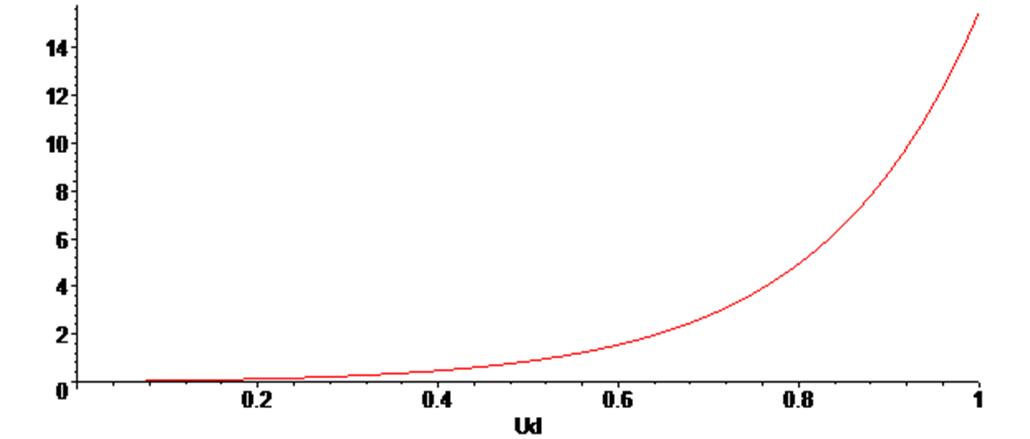
> plots [display] ( {scatterplot(X,Y), G } ) ;

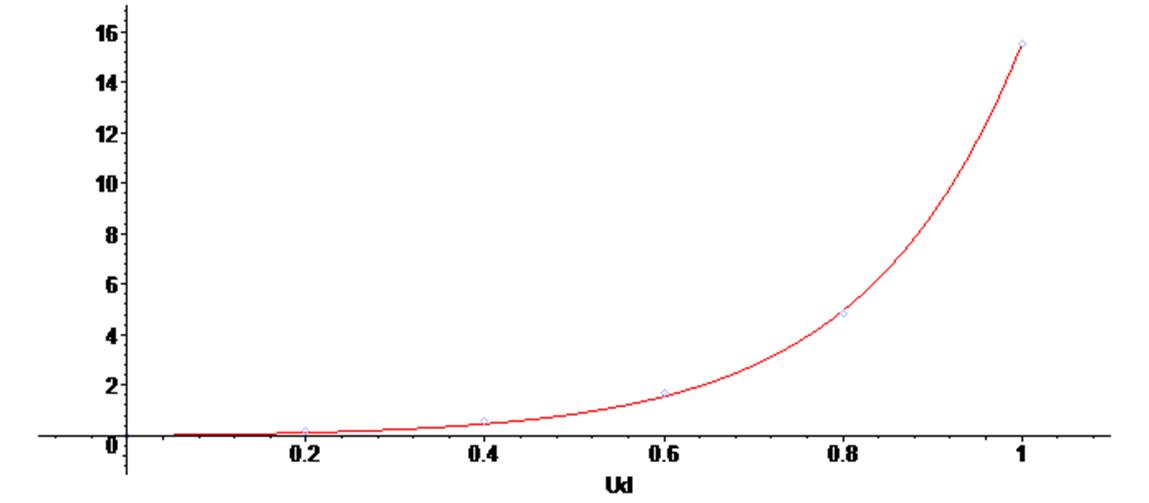
Следует заметить, что кривая нелинейной регрессии проходит не точно по заданным точкам, так как полученная зависимость - аппроксимирующая, а не интерполирующая.

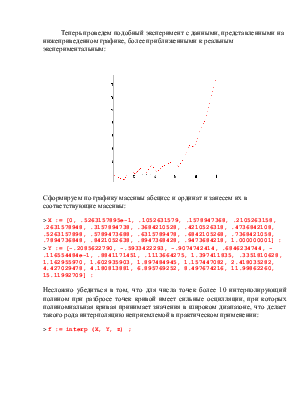
Теперь проведем подобный эксперимент с данными, представленными на нижеприведенном графике, более приближенными к реальным экспериментальным:

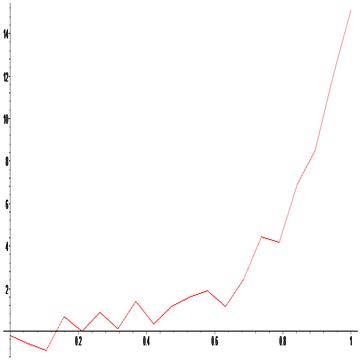
Сформируем по графику массивы абсцисс и ординат и занесем их в соответствующие массивы:

> X := [0, .5263157895e-1, .1052631579, .1578947368, .2105263158, .2631578948, .3157894738, .3684210528, .4210526318, .4736842108, .5263157898, .5789473688, .6315789478, .6842105268, .7368421058, .7894736848, .8421052638, .8947368428, .9473684218, 1.000000001] :

> Y := [-.2085622790, -.5933422293, -.9074742414, .6846234744, -.116554484e-1, .8841171451, .1113664275, 1.397411835, .3351810628, 1.162955970, 1.602935903, 1.897484945, 1.157447082, 2.418035282, 4.427029478, 4.180813881, 6.895769252, 8.497674216, 11.99862260, 15.11992709] :

Несложно убедиться в том, что для числа точек более 10 интерполирующий полином при разбросе точек кривой имеет сильные осцилляции, при которых полиномиальная кривая принимает значения в широком диапазоне, что делает такого рода интерполяцию неприемлемой в практическом применении:

> f := interp (X, Y, z) ;

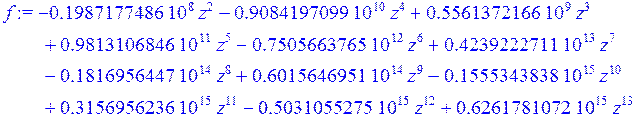
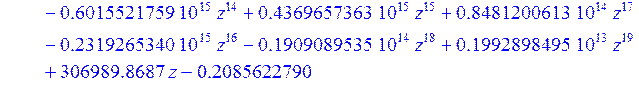
> g1 := plot (f, z = 0. .. 1) :

> g1;

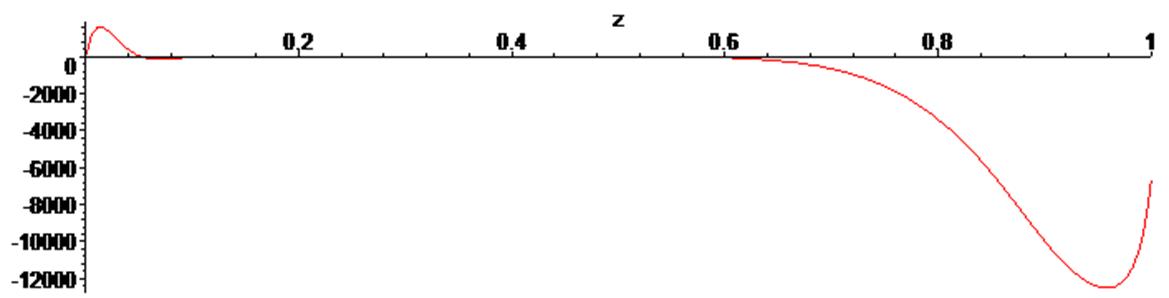
Далее выполним линейную полиномиальную аппроксимацию, выбрав полином пятой степени, и нелинейную регрессию, выбрав в качестве аналитической аппроксимирующей кривой экспоненциальную зависимость. Сравним результаты.

> f1 := fit [leastsquare [ [x,y], y = r*x^5 + k*x^4 + a*x^3 +b*x^2 +c*x + d ] ] ( [X,Y] ) ;

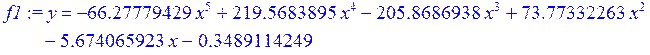
> assign (f1) :

> g := plot (y , x = 0 .. 1 ) :

> plots [display] ( {scatterplot(X,Y) , g} ) ;

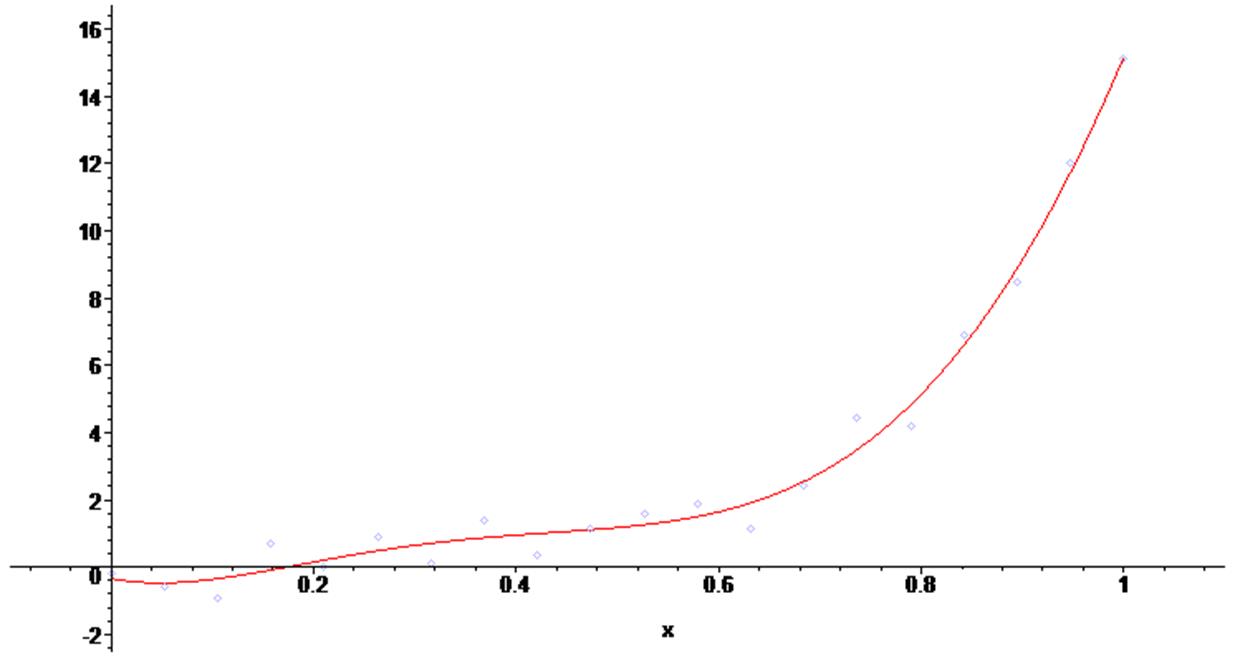
> F := NonlinearFit(I0 * ( exp (Ud/phi) - 1 ), X, Y, Ud);

> G := plot (F, Ud = 0 .. 1 , color = blue) :

> G;

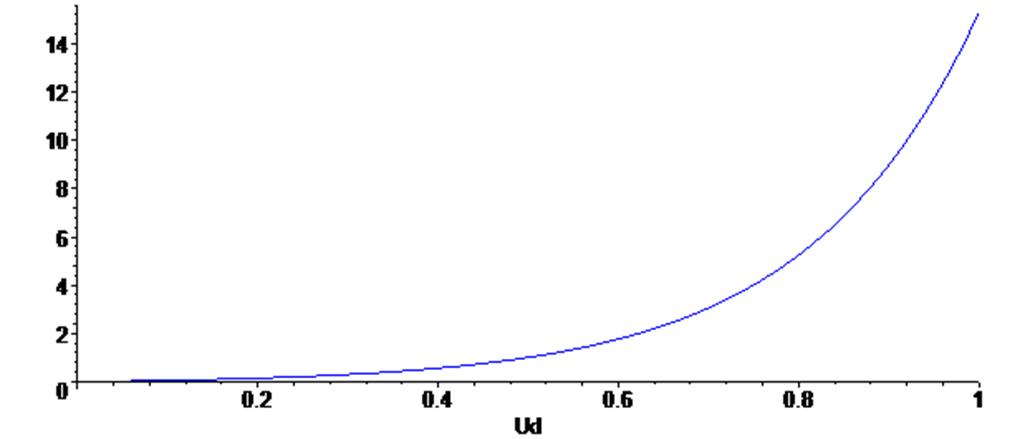
> plots [display] ( {scatterplot(X,Y), G , g } ) ;

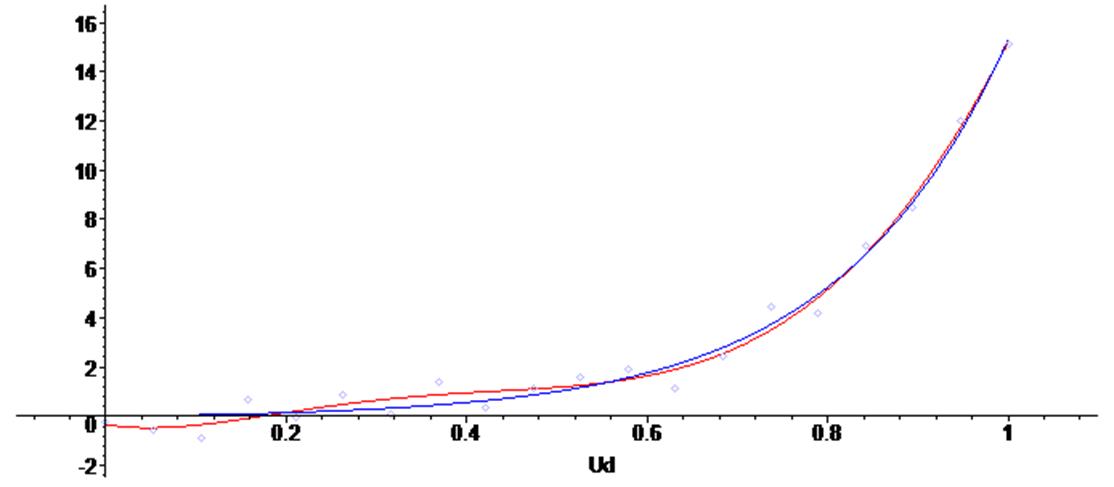
В данном случае мы видим отличающиеся результаты. Выбор более предпочтительной кривой не очевиден. Для предпочтения одной из функций следует сформулировать критерий, по которому затем можно будет выбирать оптимальные аналитические аппроксимирующие зависимости.