Пример решения систем нестационарных дифференциальных уравнений

Пример решения систем нестационарных дифференциальных уравнений

Рассмотрим схему , приведенную в примере к лабораторной работе №5, рисунок которой приведен ниже.

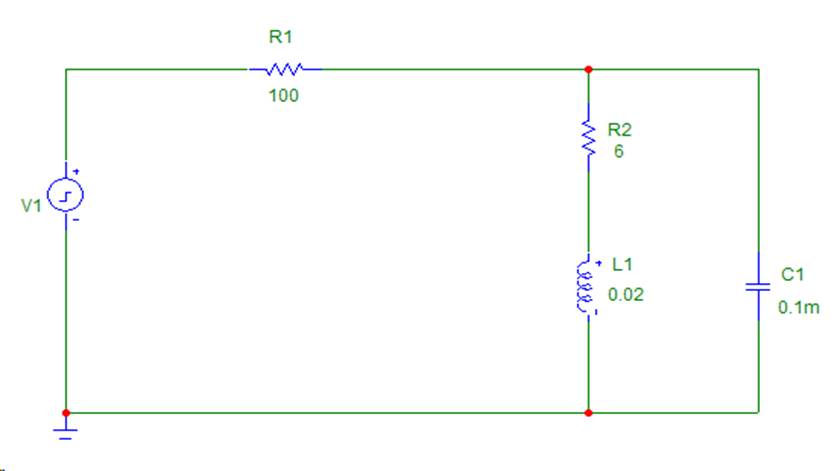
Система ОДУ, которой описывается математическая модель схемы, получена в примере к лабораторной работе №5 и выглядит следующим образом:

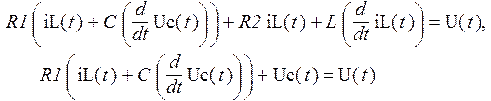
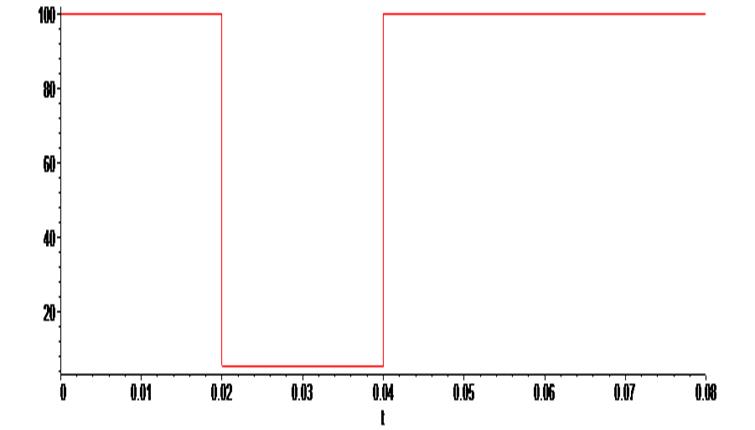
Теперь внесем изменения в схему, заменив постоянный резистор R1 резистором с изменяющимся во времени сопротивлением. Рассмотрим случай, когда сопротивление меняется от 100 Ом почти до нуля. Подобное возможно, если резистор закорачивается, например, контактами реле.

В этом случае система уравнений   будет выглядеть следующим образом:

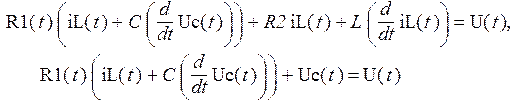
В ней учтено, что сопротивление резистора может измениться в какой-то момент времени. Такие системы ДУ, в которых коэффициенты при неизвестных непостоянны во времени, называются нестационарными, они  позволяют моделировать очень сложные реальные объекты.

Зададим сложное входное воздействие, т.е. сигнал источника V1 , и ступенчатое изменение сопротивления резистора, затем выполним моделирование.

> restart:

> with (plots) :

Warning, the name changecoords has been redefined

Warning, the name changecoords has been redefined

Задаём входной сигнал и характер изменения сопротивления резистора:

> U := (t) -> piecewise (t<0, 0, 0 <= t and t <= 0.03, sin(1047.197551*t), t > 0.03 and t < 0.05,  0, t>=0.05, 1):

> R1 := (t) -> piecewise (t<0.02, 100, 0.02 <= t and t <= 0.04, 5, t > 0.04 ,  100):

> plot ( U(t) , t = -0.0 .. 0.08) ;

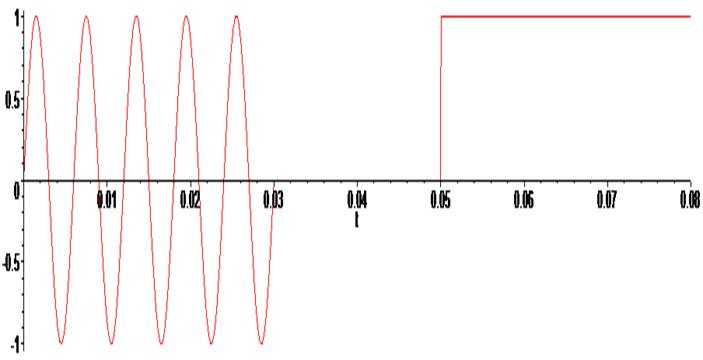
> plot ( [R1(t)] , t = -0.0 .. 0.08) ;

> Sys :=  {Nus, R1(t)*(iL(t)+C*diff(Uc(t),t))+R2*iL(t)+L*diff(iL(t),t) = U(t), R1(t)*(iL(t)+C*diff(Uc(t),t))+Uc(t) = U(t)} ;

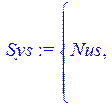
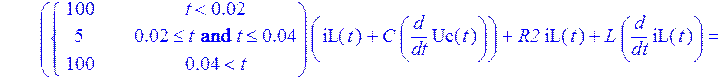
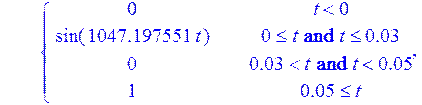
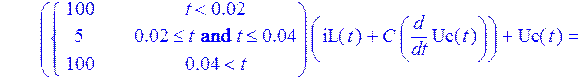
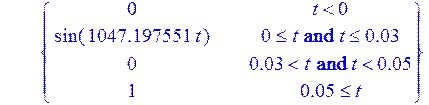
Запишем в переменную Nus начальные условия, а в переменную OD - функции, относительно которых будем искать  решение в численном виде, и зададим значения номиналов элементов для получения численного решения.

> OD :=  { Uc ( t ) , iL ( t ) } :

> Sys := subs ( Nus = ( Uc ( 0 ) = 0 , iL ( 0 ) = 0 ) , Sys ) :

> Sys;

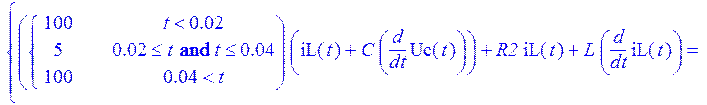
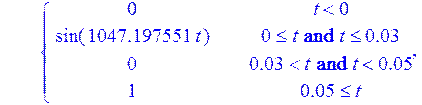
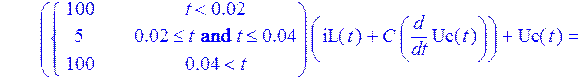
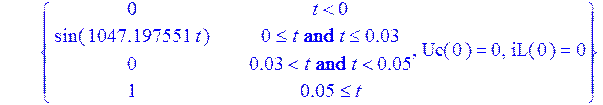
> R2 := 6: C := 0.0001: L := 0.02: 

> Rs := dsolve (  Sys   , OD, numeric ) ;

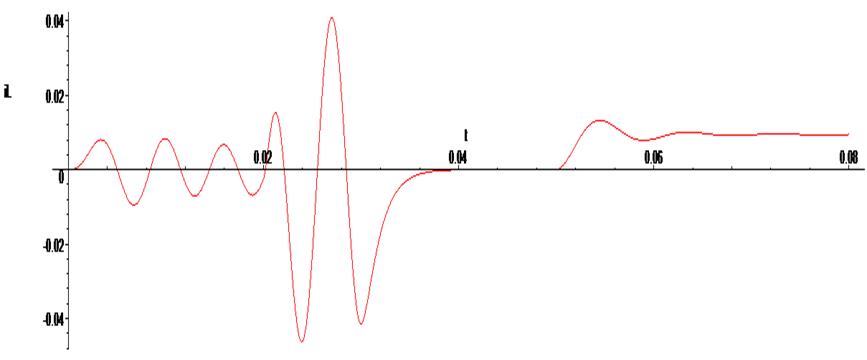
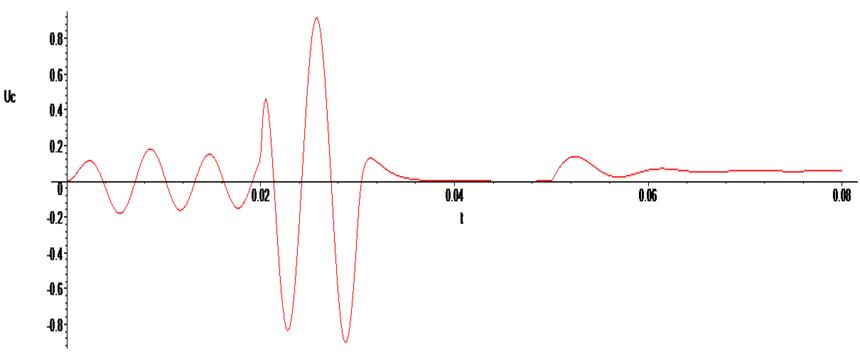
Ниже приведено решение в точке  0.015 и затем построены графики изменения напряжения на конденсаторе и тока, протекающего через индуктивность:

> Rs (0.015) ;

> odeplot(Rs,[t,iL(t)], 0..0.08 , numpoints=500);

> odeplot(Rs,[t,Uc(t)], 0..0.08 , numpoints=500);

Рассмотрим решение системы при ступенчатом изменении индуктивности. Систему уравнения запишем в форме Коши.

Форму входного сигнала оставим без изменения.

> restart: with (plots) :

Warning, the name changecoords has been redefined

> Ode :=  diff ( Uc ( t ) , t ) = ( U(t) - R1 * iL (t) - Uc (t) ) / (R1 * C) , diff ( iL ( t ) , t ) = ( Uc ( t ) - R2 * iL (t) ) / L(t) ;

> Nus1 :=  Uc ( 0 ) = 0 , iL ( 0 ) = 0 :

> OD1 :=   Uc ( t ) , iL ( t )  :

> U := (t) -> piecewise (t<0, 0, 0 <= t and t <= 0.03, sin(1047.197551*t), t > 0.03 and t < 0.05,  0, t>=0.05, 1): 

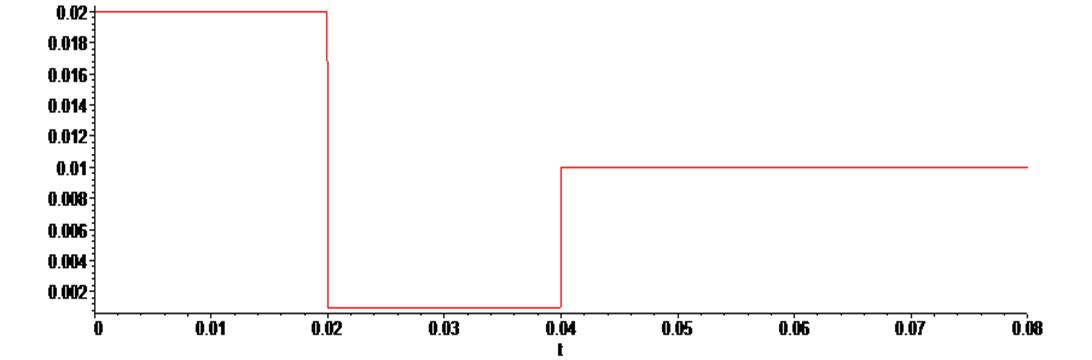
> L := (t) -> piecewise (t<0.02, 0.02, 0.02 <= t and t <= 0.04, 0.001, t > 0.04 , 0.01 ):

> plot ( U(t) , t = -0.0 .. 0.08) ;

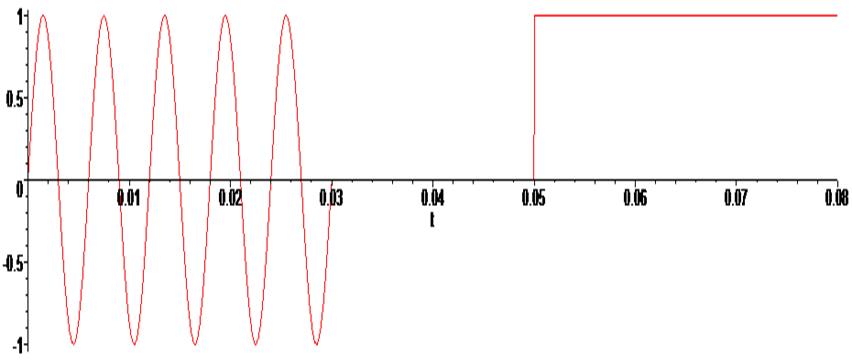
> plot ( L(t) , t = -0.0 .. 0.08) ;

> R1 := 100: R2 := 6: C := 0.0001:

> Rs1 := dsolve ( { Ode , Nus1 } , { OD1} , numeric) ;

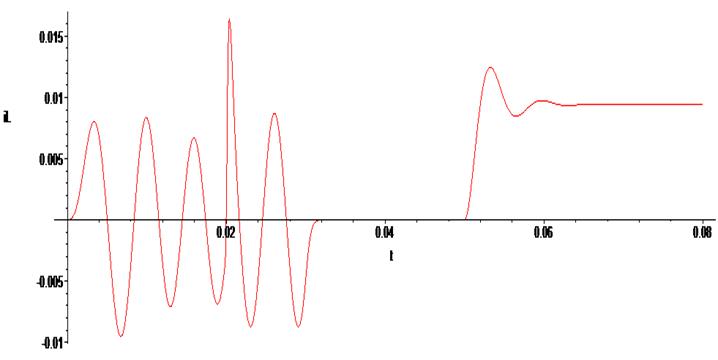
> odeplot(Rs1,[t,iL(t)], 0..0.08 , numpoints=500);

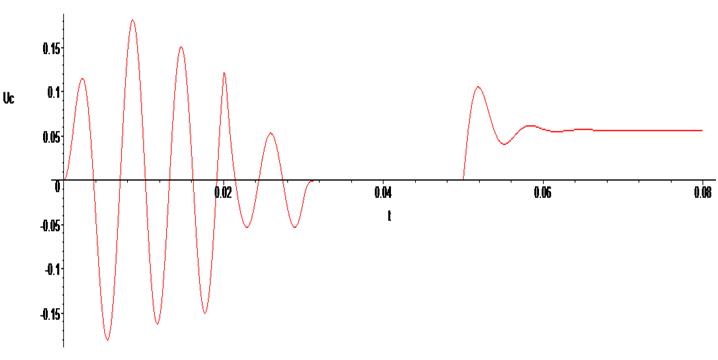
> odeplot(Rs1,[t,Uc(t)], 0..0.08 , numpoints=500);

>

Теперь усложним характер изменения значения индуктивности

Форму входного сигнала оставим без изменения.

> restart: with (plots) :

Warning, the name changecoords has been redefined

> Ode :=  diff ( Uc ( t ) , t ) = ( U(t) - R1 * iL (t) - Uc (t) ) / (R1 * C) , L(t)*diff ( iL ( t ) , t ) = ( Uc ( t ) - R2 * iL (t) ) ;

> Nus1 :=  Uc ( 0 ) = 0 , iL ( 0 ) = 0 :

> OD1 :=   Uc ( t ) , iL ( t )  :

> U := (t) -> piecewise (t<0, 0, 0 <= t and t <= 0.03, sin(1047.197551*t), t > 0.03 and t < 0.05,  0, t>=0.05, 1): 

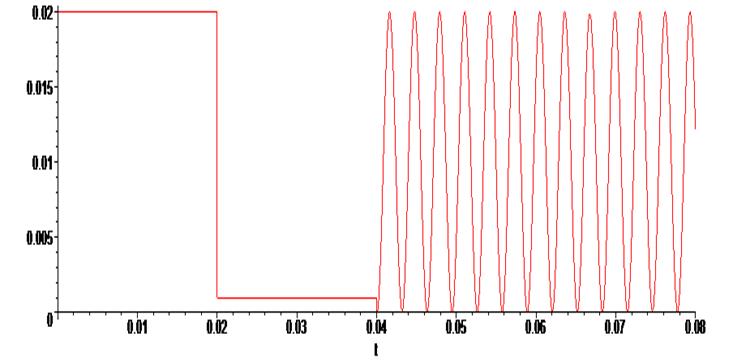
> L := (t) -> piecewise (t<0.02, 0.02, 0.02 <= t and t <= 0.04, 0.001, t > 0.04 , 0.01*sin(2000*t) + 0.01 ):

> plot ( U(t) , t = -0.0 .. 0.08) ;

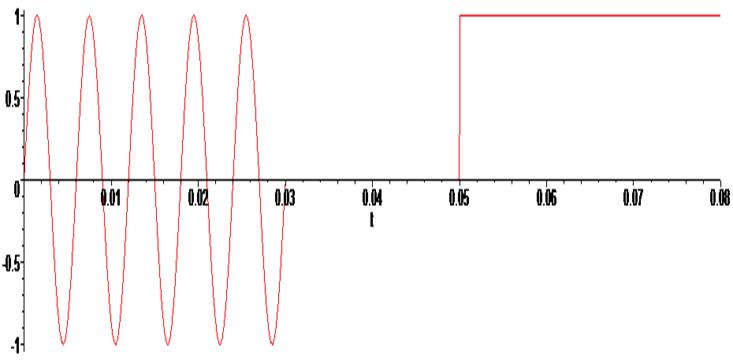
> plot ( L(t) , t = -0.0 .. 0.08) ;

> R1 := 100: R2 := 6: C := 0.0001:

> Rs1 := dsolve ( { Ode , Nus1 } , { OD1} , numeric) ;

> odeplot(Rs1,[t,iL(t)], 0..0.08 , numpoints=1000);

Warning, cannot evaluate the solution further right of .40120120e-1, maxfun limit exceeded (see ?dsolve,maxfun for details)

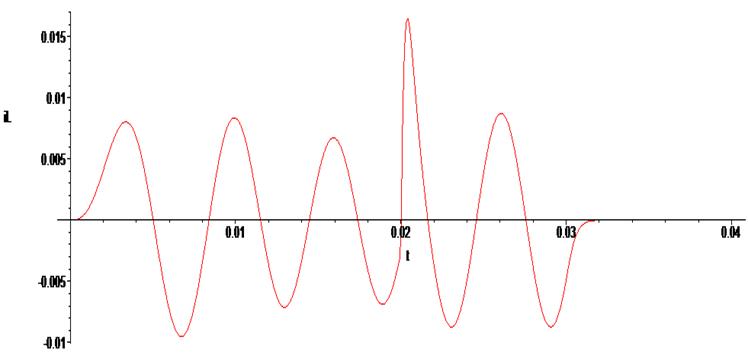
> odeplot(Rs1,[t,Uc(t)], 0..0.08 , numpoints=500);