Пример решения систем нестационарных дифференциальных уравнений, страница 2

Warning, cannot evaluate the solution further right of .40080160e-1, maxfun limit exceeded (see ?dsolve,maxfun for details)

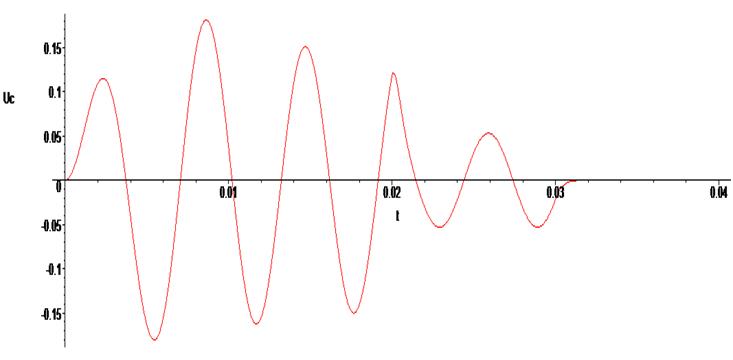
Как видим, для заданных сложных параметров системы пакет не может получить решение далее точки  t = .40080160e-1. Для поиска решения на всем интересующем временном интервале необходимо подбирать методы, изменять и при необходимости упрощать модель, решать по частям, уменьшать точность решения и применять другие доступные методы.

Попробуем уменьшить точность и задать большее число точек решения по сравнению с заданным в пакете "по умолчанию", а также, возможно,  изменить условия задачи.

> restart: with (plots) :

Warning, the name changecoords has been redefined

> Ode :=  diff ( Uc ( t ) , t ) = ( U(t) - R1 * iL (t) - Uc (t) ) / (R1 * C) , L(t)*diff ( iL ( t ) , t ) = ( Uc ( t ) - R2 * iL (t) ) ;

> Nus1 :=  Uc ( 0 ) = 0 , iL ( 0 ) = 0 :

> OD1 :=   Uc ( t ) , iL ( t )  :

> U := (t) -> piecewise (t<0, 0, 0 <= t and t <= 0.03, sin(1047.197551*t), t > 0.03 and t < 0.05,  0, t>=0.05, 1): 

> L := (t) -> piecewise (t<0.02, 0.02, 0.02 <= t and t <= 0.04, 0.001, t > 0.04 , 0.01*sin(2000*t) + 0.011 ):

> plot ( U(t) , t = -0.0 .. 0.08) ;

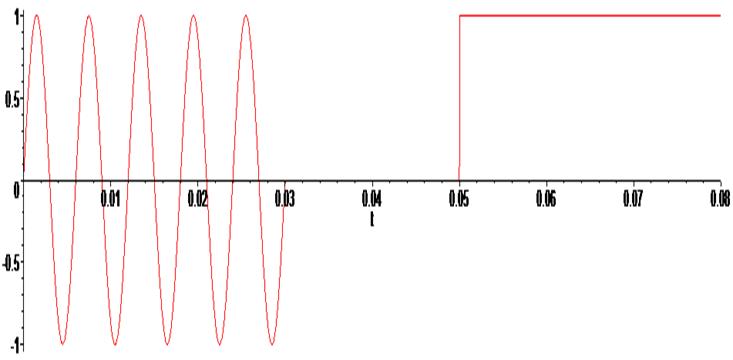
> plot ( L(t) , t = -0.0 .. 0.08) ;

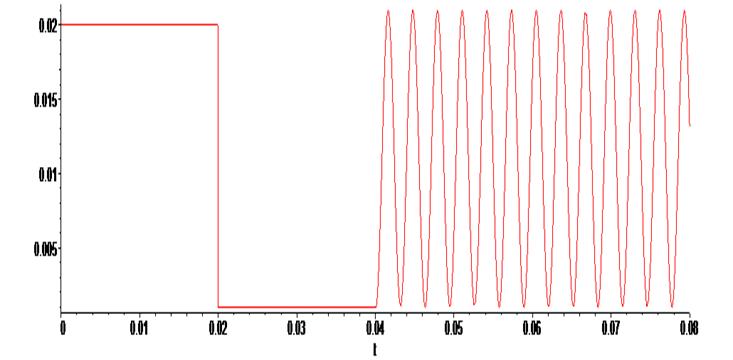
> R1 := 100: R2 := 6: C := 0.0001:

> Rs1 := dsolve ( { Ode , Nus1 } , { OD1} , numeric, range=0..0.08,  maxfun=10000000, abserr=1e-7, relerr=1e-7) ;

> odeplot(Rs1,[t,iL(t)], 0..0.08 , numpoints=500);

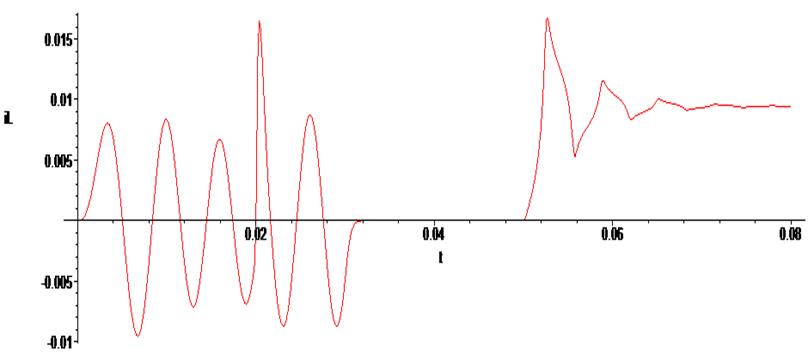
> odeplot(Rs1,[t,Uc(t)], 0..0.08 , numpoints=500);

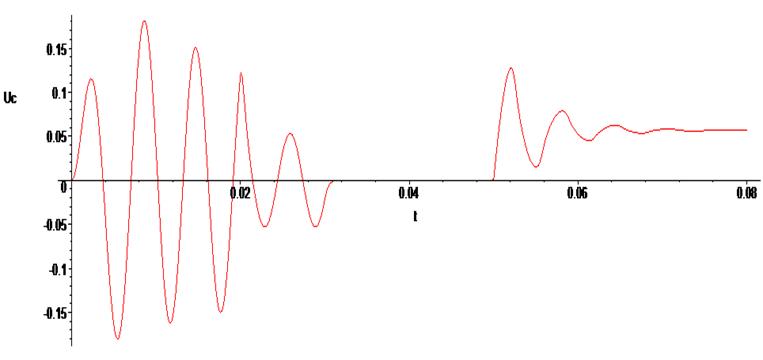
Решения добились, лишь "приподняв" синусоиду над осью абсцисс. При этом нет уверенности в том, что решение получено точное, желательно его перепроверить каким-то доступным способом. Например, прорешав в другом мощном в вычислительном плане пакете.

Рекомендуется самостоятельно провести вычислительные эксперименты, в которых увеличить амплитуду колебаний индуктивности в два раза, а затем  изменить частоты колебаний в несколько раз. Объяснить результаты экспериментов. Для получения решения следует, как и в последнем примере, к синосоиде добавить константу, чтобы она не пересекала ось абсцисс, в противном случае сложно добиться решения.

Увеличим в два раза амплитуду гармонических колебаний  индуктивности.

> restart: with (plots) :

Warning, the name changecoords has been redefined

> Ode :=  diff ( Uc ( t ) , t ) = ( U(t) - R1 * iL (t) - Uc (t) ) / (R1 * C) , L(t)*diff ( iL ( t ) , t ) = ( Uc ( t ) - R2 * iL (t) ) ;

> Nus1 :=  Uc ( 0 ) = 0 , iL ( 0 ) = 0 :

> OD1 :=   Uc ( t ) , iL ( t )  :

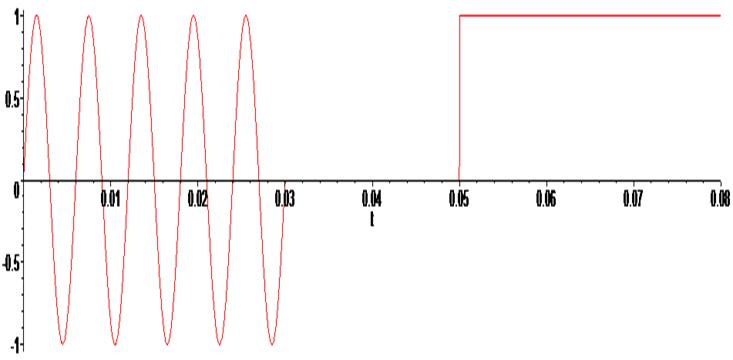
> U := (t) -> piecewise (t<0, 0, 0 <= t and t <= 0.03, sin(1047.197551*t), t > 0.03 and t < 0.05,  0, t>=0.05, 1): 

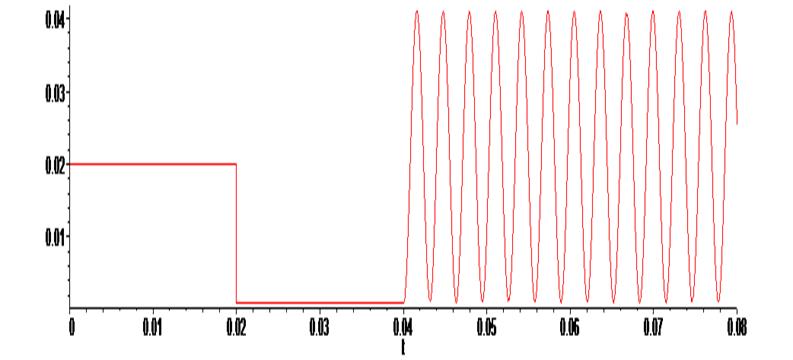
> L := (t) -> piecewise (t<0.02, 0.02, 0.02 <= t and t <= 0.04, 0.001, t > 0.04 , 0.02*sin(2000*t) + 0.021 ):

> plot ( U(t) , t = -0.0 .. 0.08) ;

> plot ( L(t) , t = -0.0 .. 0.08) ;

> R1 := 100: R2 := 6: C := 0.0001:

> Rs1 := dsolve ( { Ode , Nus1 } , { OD1} , numeric,   maxfun=10000000, abserr=1e-7, relerr=1e-7) ;

> odeplot(Rs1,[t,iL(t)], 0..0.08 , numpoints=500);

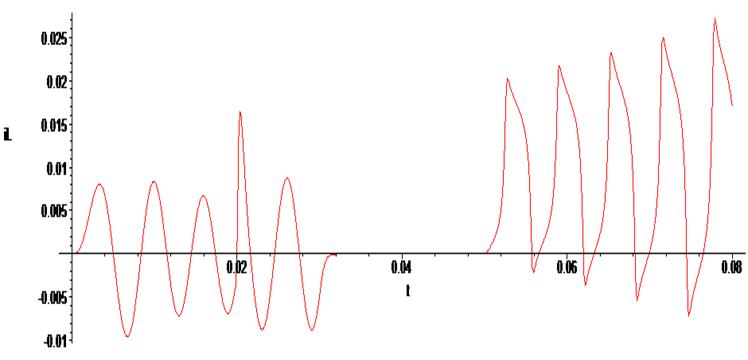
> odeplot(Rs1,[t,Uc(t)], 0..0.08 , numpoints=500);

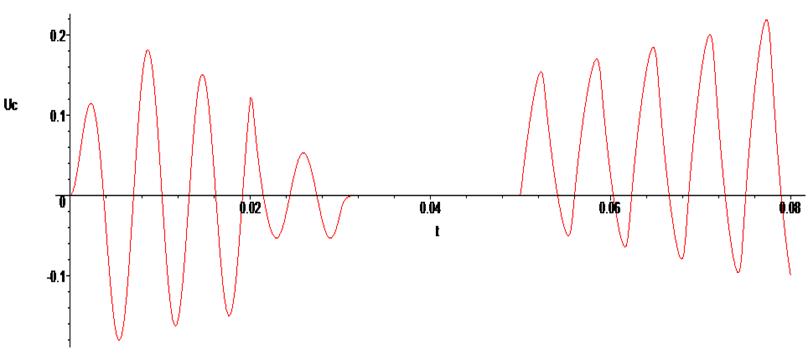
> odeplot(Rs1,[t,Uc(t)], 0. .. 0.2 , numpoints=500);

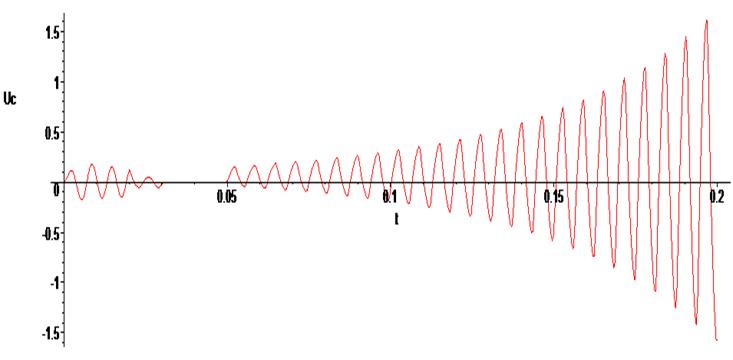
Как видим, амплитуда растет неограниченно.

А теперь гармоническое изменения индуктивности начнём после  того, как подан сигнал на вход схемы.

> restart: with (plots) :

Warning, the name changecoords has been redefined

> Ode :=  diff ( Uc ( t ) , t ) = ( U(t) - R1 * iL (t) - Uc (t) ) / (R1 * C) , L(t)*diff ( iL ( t ) , t ) = ( Uc ( t ) - R2 * iL (t) ) ;

> Nus1 :=  Uc ( 0 ) = 0 , iL ( 0 ) = 0 :

> OD1 :=   Uc ( t ) , iL ( t )  :

> U := (t) -> piecewise (t<0, 0, 0 <= t and t <= 0.03, sin(1047.197551*t), t > 0.03 and t < 0.045,  0, t>=0.045, 1): 

> L := (t) -> piecewise (t<0.02, 0.02, 0.02 <= t and t <= 0.05, 0.001, t > 0.05 , 0.02*sin(2000*t + .6250000000e-4) + 0.021 ):

> plot ( U(t) , t = -0.0 .. 0.08) ;

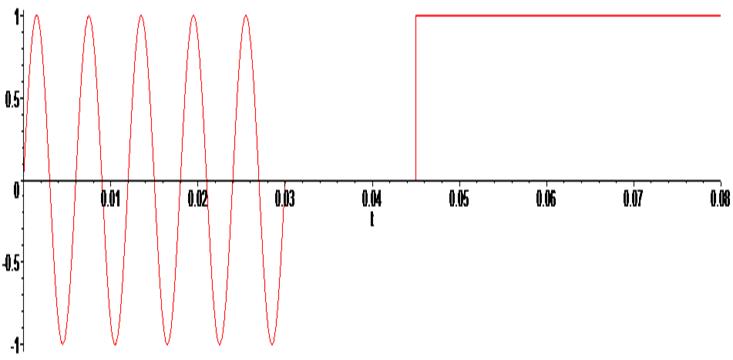
> plot ( L(t) , t = -0.0 .. 0.08) ;

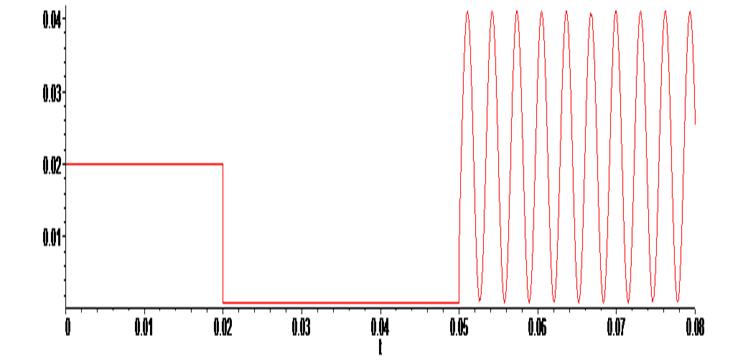
> R1 := 100: R2 := 6: C := 0.0001:

> Rs1 := dsolve ( { Ode , Nus1 } , { OD1} , numeric, maxfun=10000000, abserr=1e-7, relerr=1e-7) ;

> odeplot(Rs1,[t,iL(t)], 0..0.08 , numpoints=500);

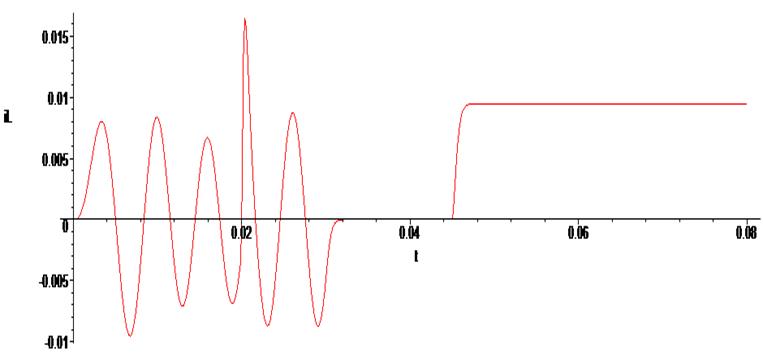
> odeplot(Rs1,[t,Uc(t)], 0..0.08 , numpoints=500);

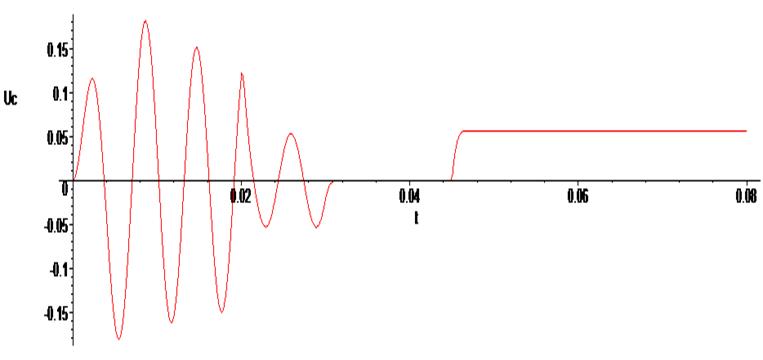
Самостоятельно продолжить вычислительный эксперимент, меняя частоты и фазы входного сигнала и колебательного процесса индуктивности.

Объяснить результаты вычислительных экспериментов!