Пример аппроксимации вольт-амперной характеристики туннельного диода методами нелинейной регрессии

Пример аппроксимации вольт-амперной характеристики туннельного диода

методами нелинейной регрессии

В начале выполним вычислительный эксперимент с кривой, заданной аналитически и точно интерполирующей ВАХ туннельного диода.

Оцифруем исходную кривую и затем по полученным данным построим аппроксимирующие кривые, после чего оценим качественно точность аппроксимации.

> restart:

> with (plots):  with ( stats [statplots] ): with(Statistics):

Warning, the name changecoords has been redefined

> Id := (U) -> .2854195919*U*exp(-.1e2*U)+.115e-7*exp(20*U)-.115e-7;

> G0 := plot (Id(U) , U = 0 .. 0.7 ):

> T := 0.7: N := 50:

> delta := T / ( N - 1 ) :

> X := array (1 .. N) : Y := array (1 .. N) :

> X[1] := 0:

> for i  from 2 by 1 to N do X[ i ] := evalf ( X [ i - 1 ] + delta ) od :

> for i  from 1 by 1 to N do  Y [i] := Id ( X [i] )  end do:

> G := plot ( [ X[n] , Y[n]  , n = 1 .. N ] ) :

Построим график исходной и оцифрованной кривой, убедимся в точности выполненной операции:

> plots [display] ( {G0,  G } ) ;

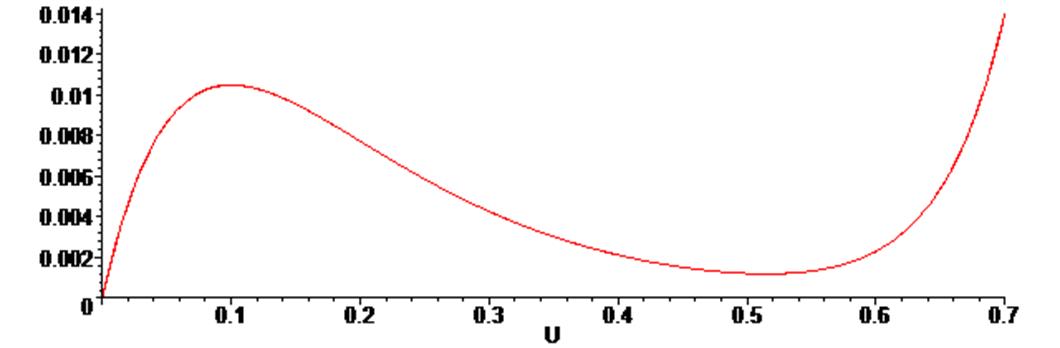
 Очевидно, что графики полностью совпадают, что подтверждает правильность дискретизации исходной функции. Абсциссы функции занесены в массив X , а ординаты - в массив - Y.

Далее получим аппроксимирующую кривую по  массивам данных абсцисс и ординат исходной кривой, воспользовавшись функций NonlinearFit библиотеки  Statistics,  и построим ее график:

> F1 := NonlinearFit( A * U * exp( -alpha*U ) + Dd * ( exp(beta*U) -1 )  , X, Y, U );

> G1 := plot (F1, U = 0 .. 0.7):

> G1;

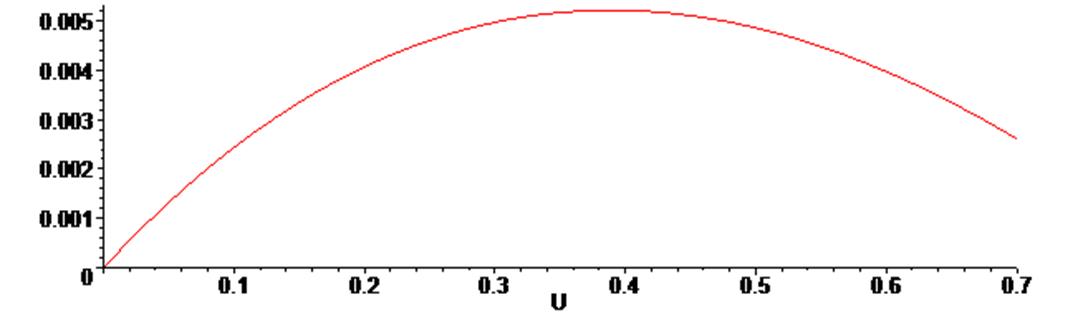
Как видим, график абсолютно не совпадает с исходным. Т.е. оптимизационный алгоритм пакета нашел некий промежуточный экстремум. Для уточнения параметров поиска зададим некоторое начальное приближение при помощи опции initialvalues, чтобы найти вариант решения, более приемлемый для нашего случая.

Полученную кривую  построим на одном поле вывода с исходной кривой и убеждаемся, что теперь параметры найдены очень точно.

> F2 := NonlinearFit( A * U * exp( -alpha*U ) + Dd * ( exp(beta*U) -1. )  , X, Y, U , initialvalues = {A = 0.20, alpha = 12, Dd = .1e-7 , beta = 15});

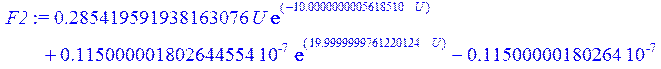
> G2 := plot (F2, U = 0 .. 0.7):

> plots [display] ( {G0,  G2 } ) ;

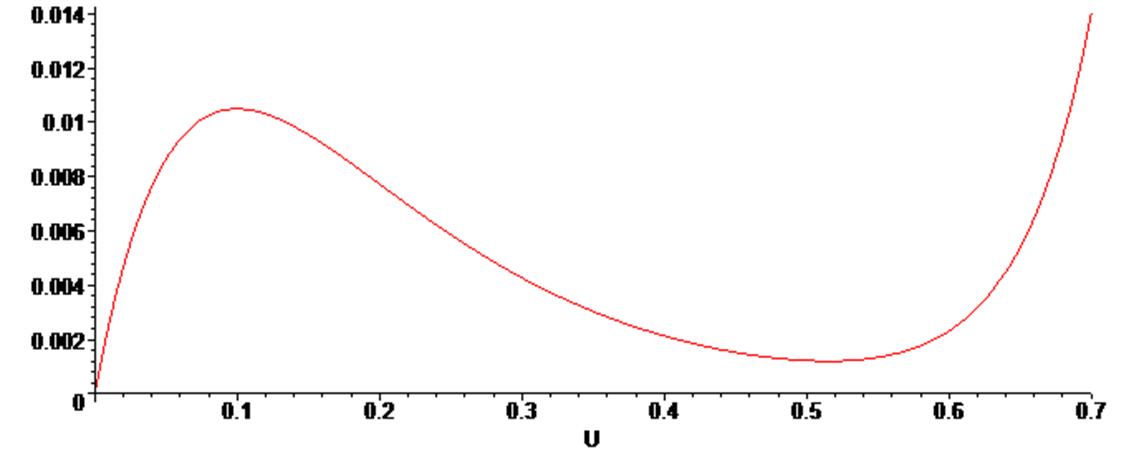
Далее найдем аппроксимирующую кривую в виде полинома 4-й степени.

> F3 := NonlinearFit(H*U^4 + A*U^3 + B*U^2 + C*U + D, X, Y, U);

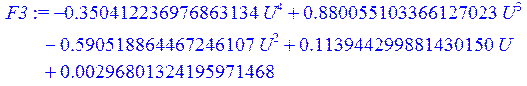
> G3 := plot (F3, U = 0 .. 0.7 , color = green ) :

> plots [display] ( {G0,  G3 } ) ;

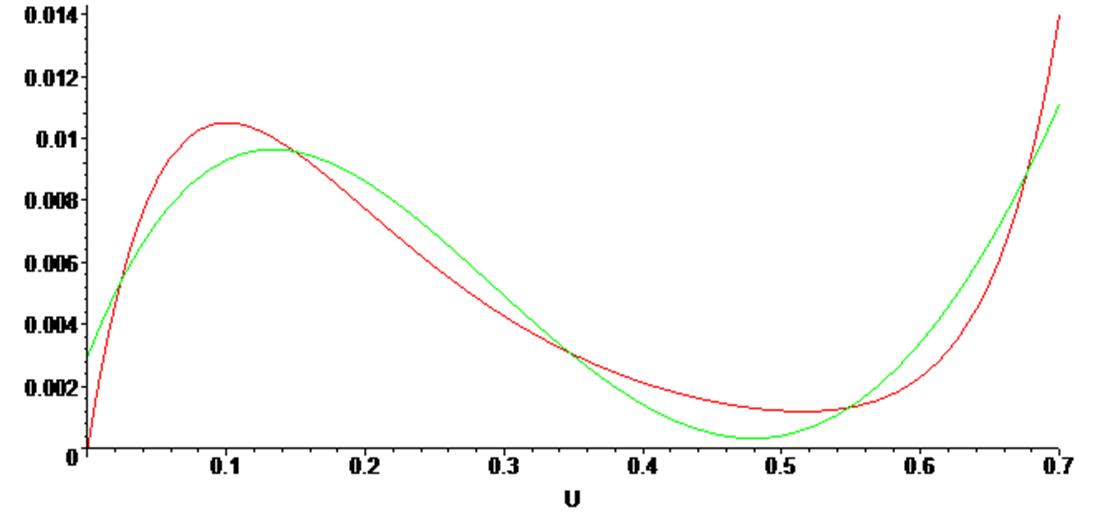
Нетрудно заметить, что в данном случае полином не так точно аппроксимировал исходную кривую.

Таким образом, в ряде случаев необходимо осознанно управлять процессом получения аналитических аппроксимирующих кривых исходя из физической сущности решаемой задачи.

Далее выполним моделирование со случайными данными.

> restart:

> with (plots):  with ( stats [statplots] ): with(Statistics):

Warning, the name changecoords has been redefined

Массивы X  и Y  -  массивы абсцисс и ординат исходной кривой.

> X := [0, 0.024, 0.049, 0.074, 0.121, 0.146, 0.194, 0.217, 0.242, 0.268, 0.294, 0.314, 0.338, 0.361, 0.386, 0.413, 0.435, 0.46, 0.483, 0.508, 0.532, 0.556, 0.579, 0.602, 0.631, 0.653, 0.7]:

> Y := [0.00052, 0.00604, 0.0092, 0.01072, 0.00966, 0.00956, 0.00728, 0.008, 0.00568, 0.005, 0.0048, 0.00448, 0.0031, 0.00368, 0.00312, 0.00204, 0.00218, 0.0014, 0.0004, 0.00032, 0.0022, 0.00196, 0.0012, 0.0016, 0.00364, 0.00468, 0.01392]:

Построим для заданных точек  экспоненциальную и полиномиальную аппроксимирующие кривые на одном поле с исходными данными. Сравним результаты.

> F2 := NonlinearFit( A * U * exp( -alpha*U ) + Dd * ( exp(beta*U) -1. )  , X, Y, U , initialvalues = {A = 0.20, alpha = 12, Dd = .1e-7 , beta = 15});

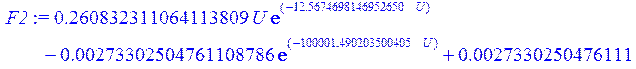
> F3 := NonlinearFit(H*U^4 + A*U^3 + B*U^2 + C*U + D, X, Y, U);

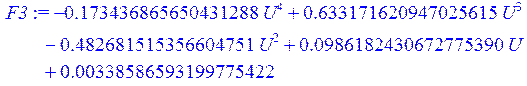
> G2 := plot (F2, U = 0 .. 0.7):

> G3 := plot (F3, U = 0 .. 0.7 , color = green ) :

> plots [display] ( {scatterplot(X,Y),  G2 } ) ;

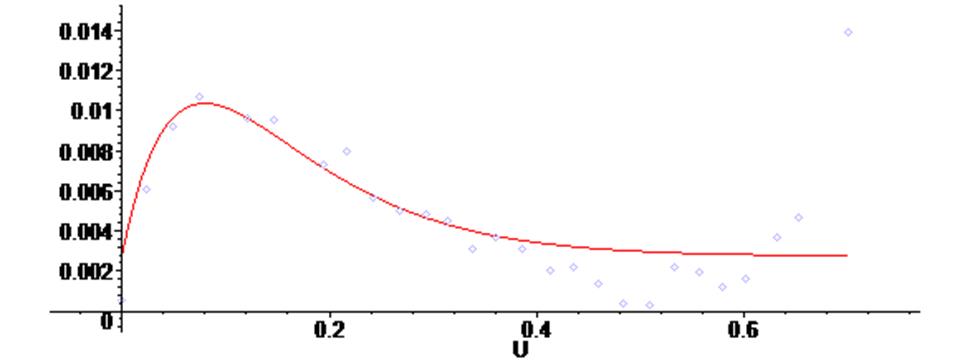
> plots [display] ( {scatterplot(X,Y),   G3 } ) ;

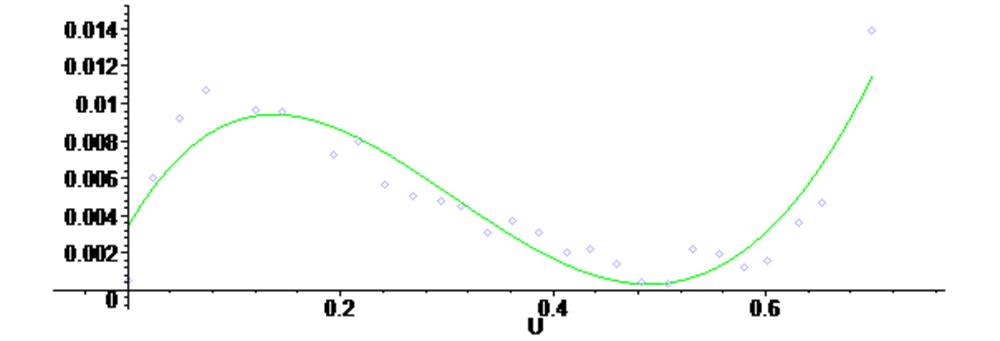
> plots [display] ( {scatterplot(X,Y),  G2, G3 } ) ;

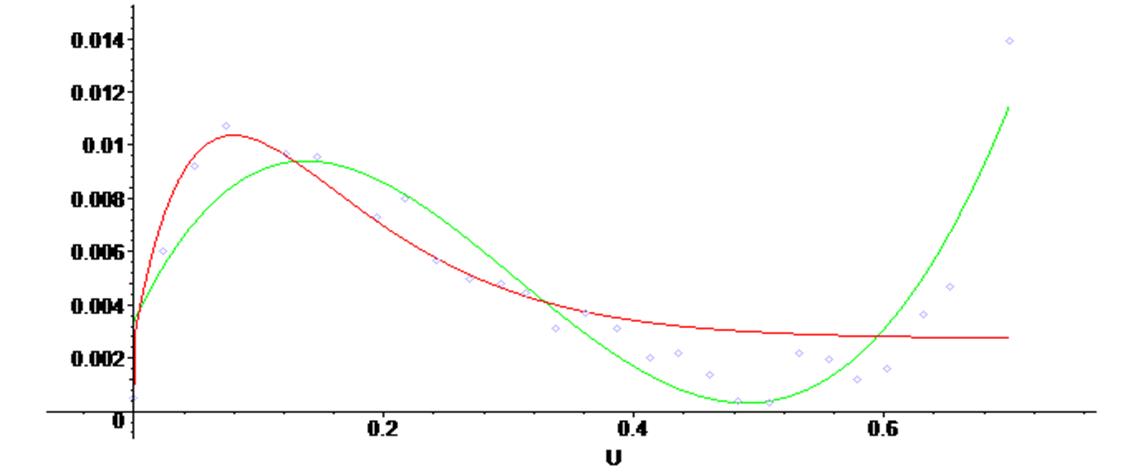
Как видим, в данном случае экспоненциальная кривая хуже аппроксимирует данные в конце графика. Это, как правило, результат их неравномерного и неточного задания, а также большого разброса параметров.

Выводы:Таким образом, выбор вида аппроксимирующей кривой - задача не тривиальная и требует от инженера математической подготовки. Для данной задачи аппроксимации сложной и неравномерно зашумлённой кривой аппроксимирующую функцию, возможно, следует искать в виде суперпозиции экспоненциальной зависимости и полиномиальной.