Пример динамического моделирования и анализа систем на примере RC-цепочки (спектральный анализ, передаточные функции, частотные характеристики)

Пример динамического моделирования и анализа систем на примере RC-цепочки

(спектральный анализ, передаточные функции, частотные характеристики)

> restart;

1. Задаём входной прямоугольный сигнал на интервале от 0 до 2*Pi и строим его график:

> st :=piecewise (t <= 0, 0, t >0 and t <= 2*Pi, 1, t > 2*Pi, 0 ) ;

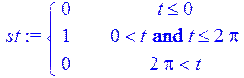
> plot (st , t = -1 .. 3*Pi ) ;

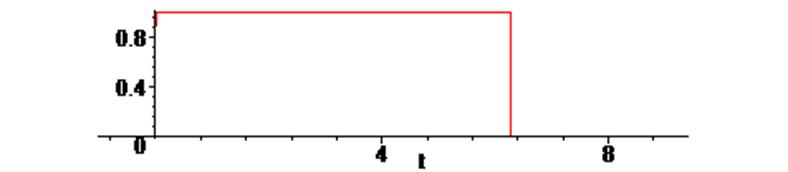
2. Вычисляем спектральную плотность сигнала и строим амплитудный и фазовый спектры сигнала:

> with (inttrans):

> Sw := fourier (st, t, w);

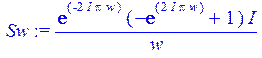
> plot (abs(Sw), w = 0 .. 20);

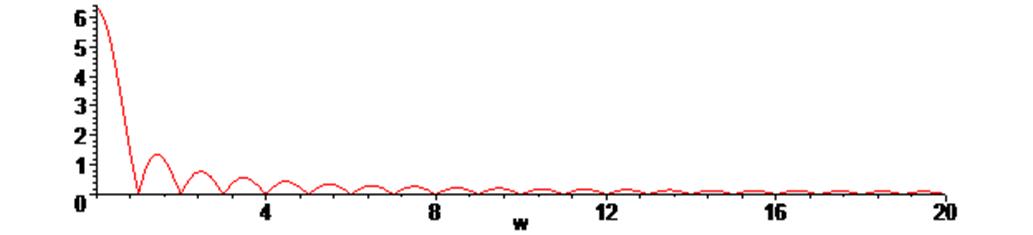
> plot (argument (Sw), w = 0 .. 20);

3. Выполняем преобразование Лапласа входного сигнала:

> Stt := laplace (st, t, p);

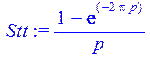
4. Записываем выражение для передаточной функции по напряжению (при этом tau = RC):

> K :=  1/(p*tau + 1);

5. Выполняем умножение изображения входного сигнала на передаточную функцию:

> U := Stt*K;

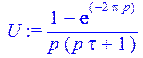
6. Выполняем обратное преобразование Лапласа произведения п.5 в результате чего получаем реакцию цепи на воздействие входного сигнала:

> Ut := invlaplace (U, p, t);

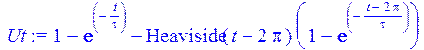
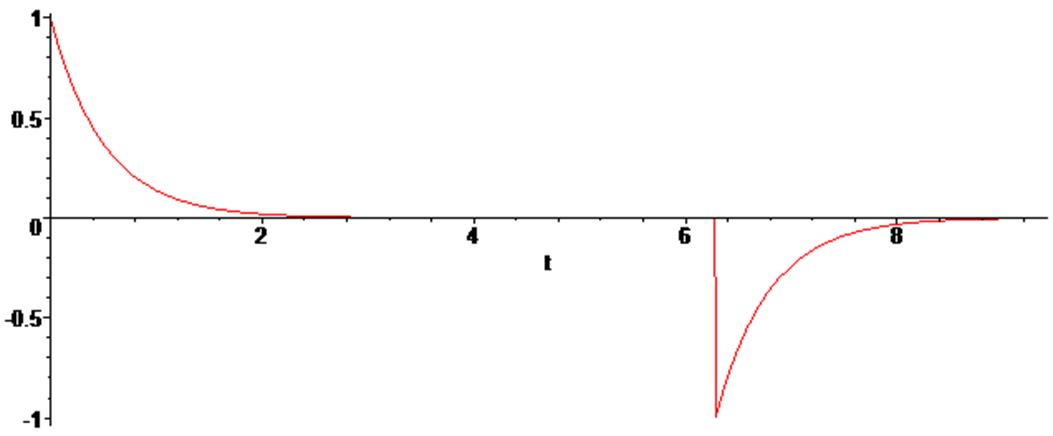
Дифференцируем реакцию цепи (т.е. выходной сигнал) на прямоугольный импульс в результате чего получаем импульсную функцию:

> Utt := diff (Ut, t);

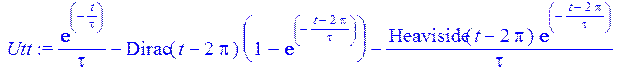
В передаточной функции выполним замену оператора р на jw в результате чего получаем амплитудно-фазочастотную  характеристику цепи :

> p := I*w;

> Kw := K;

Ниже будут построены  графики АЧХ  и ФЧХ схемы.

7. Получим выражение для  спектра выходного сигнала:

7.1 Умножением спектральной функции цепи на спектр входного сигнала:

> Utw := Kw*Sw;

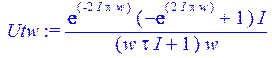
7.2 Через преобразование Фурье:

> Utwf := fourier (Ut, t, w);

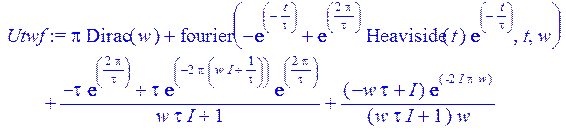
8. Построить графики выходного сигнала, его спектр, а также АЧХ цепи.

Задаём значение tau = 0.5 и строим графики входного, выходного сигналов, продифференцированного выходного сигнала на одном поде вывода:

> tau := 0.5:

> plot ([st, Ut, Utt], t = 0 .. 3*Pi);

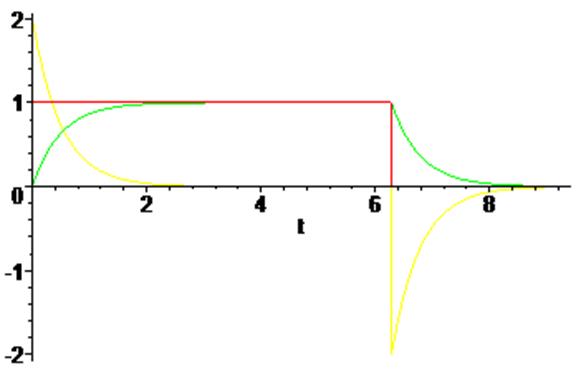
График АЧХ спектральной плотности выходного сигнала:

> plot (abs (Utw), w = 1 .. 20);

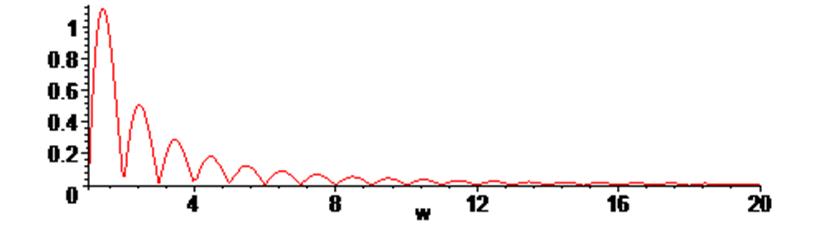
Графики  АЧХ  и ФЧХ цепи:

> plot ( abs (Kw), w =  0 .. 20 ) ;

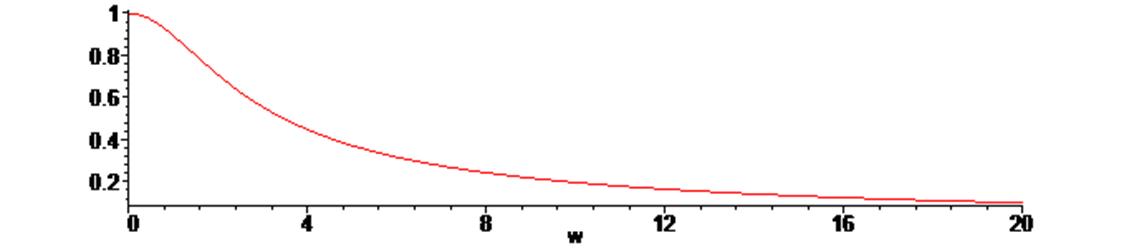
> plot ( argument (Kw), w =  0 .. 20 ) ;

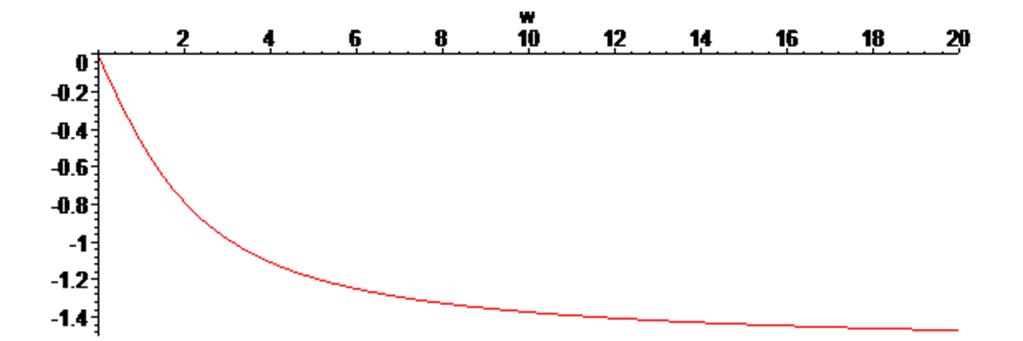
9. Выполним анализ реакции цепи на входной сигнал решением дифференциального уравнения при нулевых начальных условиях:

> Du := diff (Uc(t), t) * R*C + Uc(t) = st;

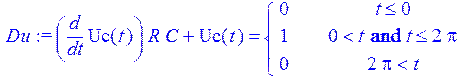
> Nu := Uc(0) = 0:

> Rdu := dsolve ({Du , Nu}, Uc(t) );

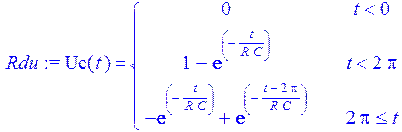
> assign (Rdu);

> Uc(t);

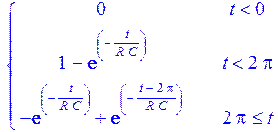
> with (plots):

Присвоим значения параметрам цепи R и C и построим график изменения выходного напряжения (т.е. на конденсаторе), а также входного и выходного на одном поле вывода:

> R := 1: C := 0.5:

> plot (Uc (t), t = 0 .. 3 * Pi);

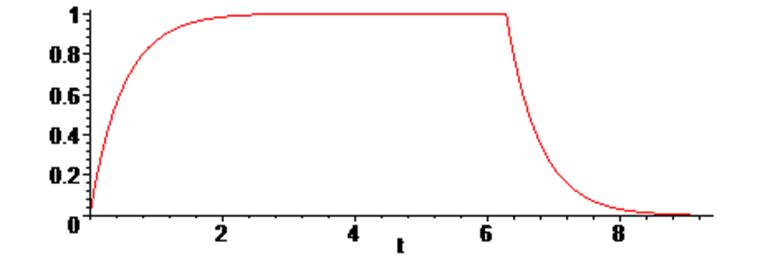
> plot ([Uc(t), st], t = 0 .. 3 * Pi);

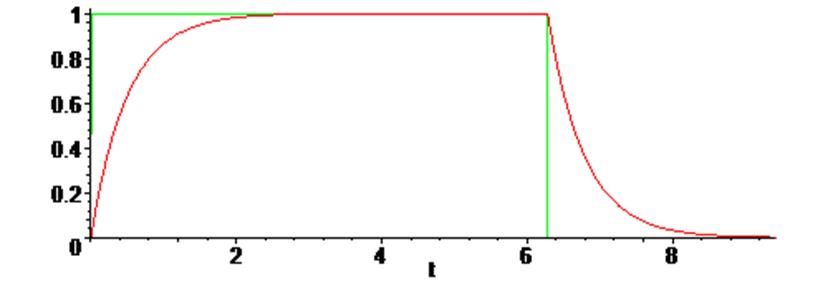
Убеждаемся в идентичности результатов анализа, выполненного через преобразование Лапласа и путём решения дифференциального уравнения!

Графики изменения напряжение на резисторе и тока через него можем построить следующим образом:

> plot ([  st - Uc(t) ], t = 0 .. 3 * Pi);

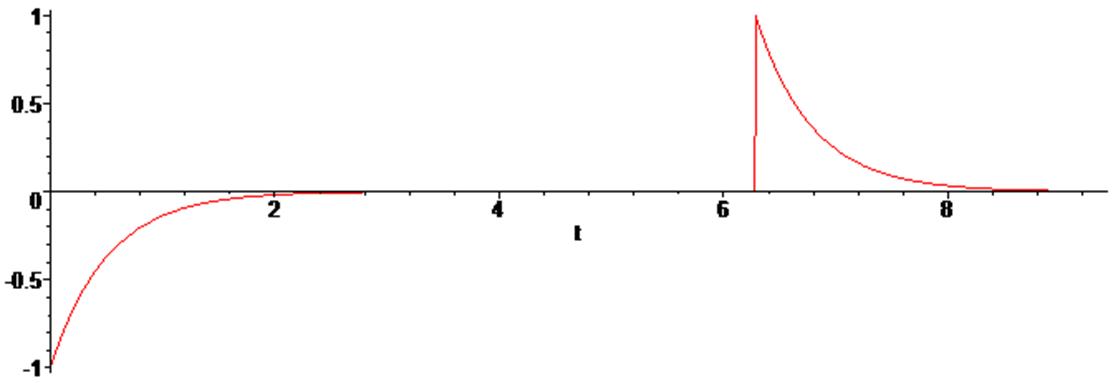
> plot ([ (st -Uc(t))/R ], t = 0 .. 3 * Pi);

>