Построение математической модели движения локомотива, анализ основных показателей, страница 3

Рассмотрим процесс интегрирования уравнения  движения поезда. В  диссертационной работе Дениско [10] для интегрирования дифференциального уравнения движения поезда используются различные численные методы: Эйлера, Рунге-Кутта, Адамса, Чаплыгина и др. Автор использует метода Эйлера для решения дифференциального уравнения движения поезда, а также предлагает рекомендации для выбора оптимального шага  интегрирования S_u = 10 м для построения кривой разгона и DS_u = 50 м при расчете основной кривой движения поезда.

Однако такой  шаг интегрирования является слишком малым при выполнении тяговых оптимизационных расчетов на  ЭВМ, когда для  выбора  оптимальных режимов ведения n_кj требуется перебор большого количества вариантов. В работах А.М. Костромина [16,17] предлагается  новый  нетрадиционный метод интегрирования дифференциального уравнения движения поезда, который может быть назван методом линейной аппроксимации правой части дифференциального уравнения.  В методе Эйлера правая часть дифференциального уравнения (производная  F (n_к, RE, V))  на  шаге  интегрирования  DS  рассматривается  как постоянная.

Система дифференциальных уравнений (2.3) решается нетрадиционным методом линейной аппроксимации правой части уравнения, разработанного в БелГУТе, который позволяет в 10–20 раз увеличить шаг интегрирования по сравнению с известными в математике методами Эйлера, Рунге-Кута и др []. и существенно в 4–8 раз уменьшить время расчета на ЭВМ, что позволило довести шаг интегрирования до величины шага варьирования.[24]

Расчетные формулы интегрирования уравнений движения поезда нетрадиционным методом имеют следующий вид[17,23,24]:

                                  (2.5)

где V₀ – скорость в начале шага интегрирования;

 V₁ – скорость в конце шага интегрирования;

DS – шаг интегрирования;

P^/ – признак направления движения поезда;

P^/=1 при движении поезда в прямом направлении, P^/ =-1 при движении в обратном направлении.

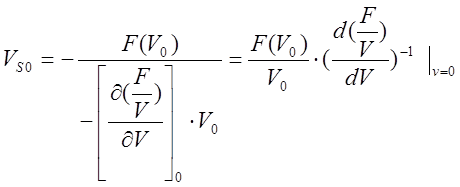                                        (2.6)

Частная производная в шаге интегрирования

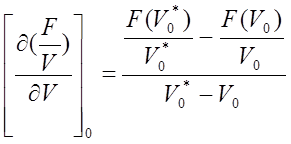                                                                                  (2.7)

где V₀^* = V₀ + DV – скорость поезда, достаточно мало отличающаяся от начальной         скорости V₀.

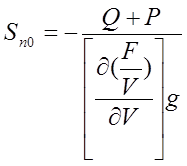                                                (2.8)

Время на шаге интегрирования DS:

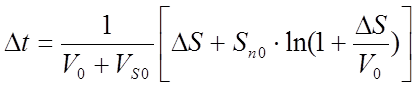                         (2.9)

Для проведения исследований по оценке выполнения графика движения  поездов и экономии топлива необходимо моделировать процесс движения поезда по  участку.  Тяговые  расчеты ориентированы на использование максимальной мощности локомотива, в результате чего для поезда расчетной массы Qр  определяют кривую скорости, время хода и расход топлива.

2.4. математические методы при расчете оптимальных режимов ведения

Для расчета оптимального процесса ведения поезда по заданному участку можно использовать различные математические методы теории оптимального управления, вариационное исчисление, метод равновесных скоростей, метод динамического программирования, принцип максимума Понтрягина, метод локальных вариаций и т.д.[7,11,12,14,16,17,18,19,23,24,27]

Можно выделить два математических метода, которые получили наибольшее распространение при расчете оптимального процесса ведения поезда по участку. Это метод динамического программирования и принцип максимума Понтрягина. Общими для этих двух методов являются следующие положения:

-  при расчете оптимальных режимов ведения расчетный участок разбивается на шаги варьирования DS_j (наименьшие элементы профиля с неменяющимся уклоном, в пределах которых режим ведения остается неизменным).

-  величину шага варьирования следует принять в диапазоне DS_j = 500 – 1000м.

Для оптимизации минимизируют величину расхода топлива в рамках заданного графиком движения времени хода.

Рассмотрим метод динамического программирования.

  В координатной плоскости V – (скорость), S – (путь) строится сетка с интервалом V^с по вертикали, а по горизонтали выделяют шаги варьирования DS_j. Условием оптимальности в каждой точке координатной сетки будет выражение[7,23,24,25,27]:

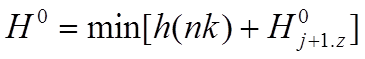                                                           (2.10)

                nk,j_T

где h(nk) – критерий, оценивающий траекторию движения поезда на данном шаге;

H⁰_j+1.z – критерий оптимальной стратегии дальнейшего управления движением поезда от точки Z в конце данного шага до конечного состояния объекта управления.