Построение математической модели движения локомотива, анализ основных показателей, страница 2

2. построение математической модели ДВИЖЕНИЯ  локомотива, анализ основных показателей

Чтобы  выполнить эти расчеты необходимо иметь характеристики тепловоза, данные о поезде, а также профиля пути и информацию о заданных остановках.

2.1. ТЯГОВЫЕ И РАСХОДНЫЕ ХАРАКТЕРИСТИКИ ТЕПЛОВОЗА.

Математическую модель движения тепловоза можно построить по тяговым и расходным характеристикам.

Тяговая характеристика тепловоза имеет следующий вид (рисунок 2.1),  а  расходная представлена следующим образом (рисунок 2.2).

 Где,

       Fк - сила тяги;

       V - скорость движения;

       Gч - удельный (часовой или минутный) расход топлива;

При расчете   на   ЭВМ, кривые   зависимостей  Fк = f(n_k,RE), описываются математическими формулами [23,24]:

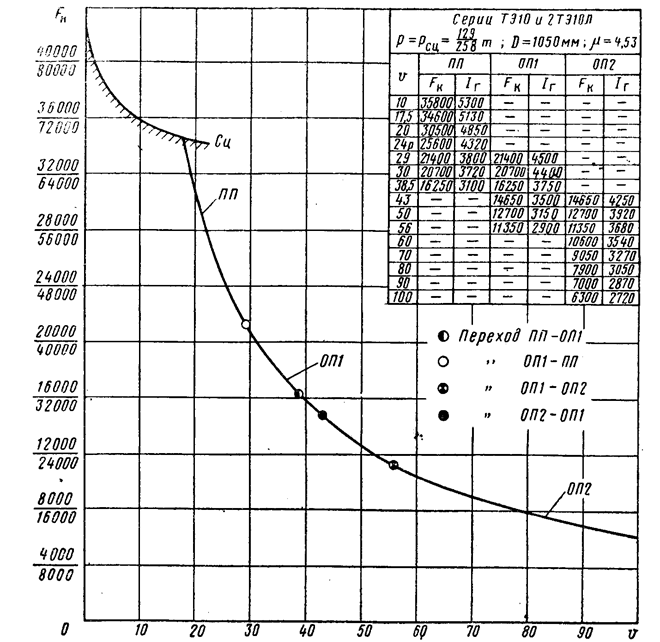Рисунок 2.1 – тяговые характеристики тепловозов ТЭ10 (цифры в числителе) и 2ТЭ10Л (цифры в знаменателе)

                                (2.1)

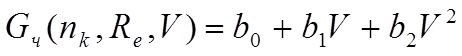  (2.2)

где F_k – сила тяги тепловоза;

G_ч – удельный (часовой) расход топлива;

n_k – позиция контроллера;

R_e – режим ослабления тяговых электродвигателей (ТЭД);

а₀, а_1, а₂ – коэффициенты математических формул, определяемые для каждой кривой F_k(V) по методу наименьших квадратов [];

b₀, b_1, b₂ – аналогичные коэффициенты для кривых G_ч.

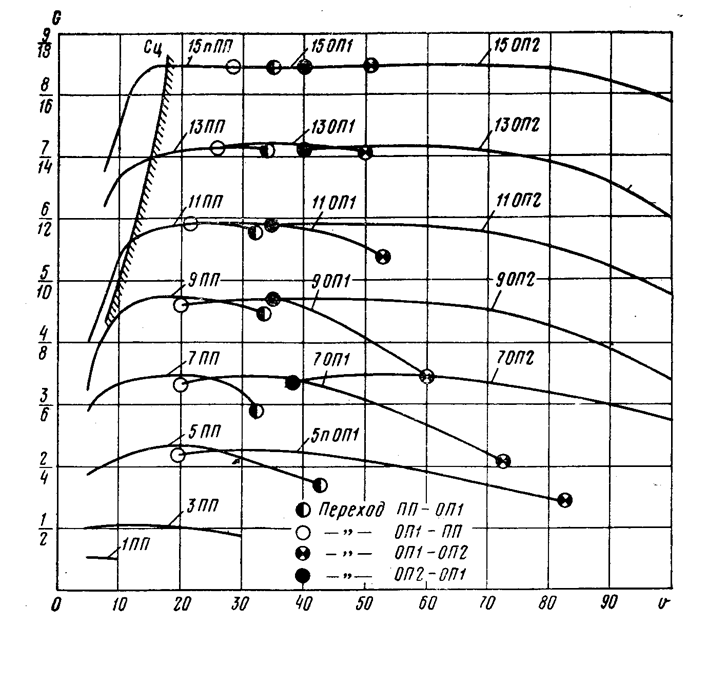
Рисунок 2.1.2. Расход топлива в режиме тяги тепловозами ТЭ10 и 2ТЭ10Л. В числителе ординат данные относятся к тепловозу ТЭ10, в знаменателе – к тепловозу 2ТЭ10Л.

в упрощенной математической модели тепловоза параметром R_e можно пренебречь.

2.2. математическая модель движения поезда по участку

Для проведения исследований по оценке экономии топлива необходимо моделировать процесс движения поезда по  участку. Тяговые  расчеты ориентированы на использование максимальной мощности локомотива, в результате чего для поезда расчетной массы Q_р  определяют кривую скорости, время хода и расход топлива.

При выполнении графика движения поезда машинист, ведя поезд, использует  не  только  и  не столько полную мощность тепловоза, сколько промежуточные режимы ведения

nк(nк(min)<=nк<=nк(max))

Для  проведения машинных экспериментов необходимо иметь модель движения поезда,  более точно отражающую реальный физический  процесс по сравнению с результатами тяговых расчетов.

Математическая модель  движения  поезда по участку на основании второго закона  Ньютона  можно представить как систему дифференциальных  уравнений:

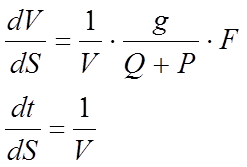              (2.3)

где Q,P – соответственно массы состава и локомотива;

F – равнодействующая сил приложенных к поезду:

     (2.4)

где W₀^/, W₀^// – полное основное сопротивление локомотива и вагонов при движении поезда;

W_i – сопротивление движению от уклона пути;

B_T – тормозная сила;

j_T – параметр, определяющий интенсивность торможения.

Расчетные формулы определения W₀^/, W₀^//, W_i, B_T, имеются [20].

Решение систем уравнений численными методами позволяет получить кривую скорости V = f (S) или V = f (t).  Применяя математические методы оптимального управления,  можно  с помощью данной  модели в рамках заданного времени хода определять такие режимы ведения n_кj,  чтобы расход  топлива  был минимальным.

В состав модели движения поезда  по участку входит математическая модель локомотива, представляющая собой его выходные характеристики:  F_к = f₁ (n_к, RE, V) и расходные G_ч = f₂ (n_к, RE, V).

2.3. анализ существующих методик получения математических моделей движения поезда

для решения системы  дифференциальных  уравнений (2.3) с помощью численных методов каждый элемент профиля  DS_в разбивается на  шаги  интегрирования DS_u (при интегрировании по пути) или Dt_u (при  интегрировании  по  времени). Под шагом варьирования режимов ведения поезда понимают такой отрезок пути DS_в, на котором режим движения n_к не может изменится. Как показывают [12]  исследования  Е.В. Ерофеева в своей диссертационной работе, при выполнении тяговых оптимизационных расчетов на ЭВМ величину шага варьирования следует принимать равной S_в = 500...1000 м.

В процессе решения дифференциальных уравнений движения поезда при использовании математической модели поезда определяют, исходя из начальной скорости V₀,  конечную скорость V₁, а также время Dt_в (или путь DS_в) и расход топлива G_в для каждого шага интегрирования. В данной работе моделирование движения поезда при построении основной кривой и кривой торможения осуществляется по пути. Расчет ведется с учетом ограничений скорости и остановок.