зависимости от вида представления сообщений на входе и выходе канала связи различают непрерывные, дискретные и полунепрерывные каналы связи.
В непрерывных каналах связи сообщения на входе и выходе представлены в аналоговой или дискретно-аналоговой форме. Простейшим непрерывным каналом связи является пара проводов, по которым передаются электрические сигналы.
В дискретных каналах связи сообщения на входе и на выходе представлены в цифровой форме. Такой канал обычно состоит из непрерывного канала, к которому на входе подключаются устройства формирования и кодирования цифровых сигналов, а на выходе – решающее устройство. Последнее служит для опознавания переданных сигналов. Включение решающего устройства в канал вызвано тем, что в результате воздействия помех сигналы на выходе канала всегда образуют непрерывное множество (даже при дискретном множестве входных сигналов)
Решающее устройство необходимо для преобразования непрерывного множества принимаемых сигналов в дискретное множество выходного алфавита канала связи. В теории информации дискретный канал рассматривается как некоторое устройство со
![]()
тогда
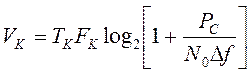
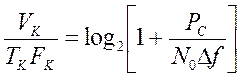
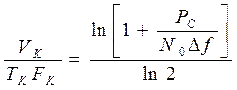
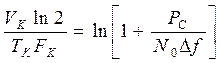
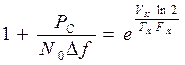
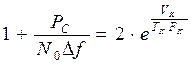
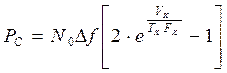
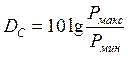
где ![]() -
максимальное значение мощности реализации сигнала длительностью
-
максимальное значение мощности реализации сигнала длительностью ![]() , полученное усреднением во времени;
, полученное усреднением во времени; ![]() -
минимальное значение мощности реализации сигнала длительностью
-
минимальное значение мощности реализации сигнала длительностью ![]() , полученное усреднением во времени.
, полученное усреднением во времени.
Практически в условиях шумов в канале уровень мощности
определяется средней мощностью шумов в канале ![]() и тогда
можно написать
и тогда
можно написать
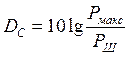
Аналогично физическому объему сигнала можно ввести и характеристику, называемую физическим объемом канала или емкостью канала
![]() (*)
(*)
Здесь Tk – время использования канала; Fk – полоса пропускаемых каналом частот; Dк – динамический диапазон уровней сигналов, пропускаемых каналом с допустимыми искажениями.
Для гауссова канала
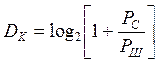 (**)
(**)
Выразим предельную мощность сигнала, который может быть передан по данному каналу, если физический объем канала Vk c полосой Fk, если его использовать в течение Tk секунд.
Из формул (*) и (**)
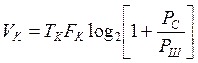
Кроме того
статическими (вероятностными) связями между входом и выходом, отражающими действие помех. При этом процессы модуляции, демодуляции и принятия решения обычно исключаются из рассмотрения.
В полунепрерывных каналах на одном из концов (входе или выходе) сообщение может быть представлено в
цифровой форме, а на другом – в аналоговой или дискретно аналоговой.
Канал передачи информации характеризуется:
- входным алфавитом (Ak), который должен соответствовать алфавиту источника информации, в противном случае между источником и каналом необходимо установить кодирующее устройство, согласующее алфавиты. Это кодирующее устройство можно считать элементом источника, либо канала;
- выходным алфавитом (Bk), который из-за воздействия помех может не совпадать с входным алфавитом;
- скоростью передачи информации, которая определяется средним количеством информации, передаваемым по каналу в единицу времени;
- пропускной способностью, максимально возможной для данного канала скоростью передачи информации.
Будем полагать, что на вход канала (от непрерывного источника) поступают непрерывные сигналы U(t), а с выхода снимаются непрерывные сигналы z(t).
Общие выражения, определяющие скорость передачи и пропускную способность непрерывных каналов, имеют такой же вид, как и в случае дискретных каналов, с той лишь разницей, что вместо энтропии множества знаков здесь используются дифференциальные энтропии на один независимый отсчет
![]()
где h(H) – дифференциальная энтропия на один отсчет сигнала U(t); h(z/U) – условная дифференциальная энтропия отсчета z(t) при известном отсчете U(t).
Если в канале действует аддитивная помеха N(t) так, что
![]() ,
,
то h(Z/U) = h(N) – дифференциальная энтропия на один отсчет помехи, ибо при заданном U(t)
неопределенность отсчета Z(t) определяется исключительно неопределенностью отсчета помехи.
Следовательно, количество переданной на один отсчет информации в непрерывном канале с аддитивным шумом
![]()
Если в канале с
полосой пропускания ![]() действует стационарный гауссовский шум, статистически
независимый от полезного сигнала, то h(t) не зависит от выбора вида сигнала и скорость передачи
информации R будет максимальна, если h(U) максимальна. Это
условие выполняется, если полезный сигнал U(t) также будет гауссовским
процессом. При этом скорость передачи информации
действует стационарный гауссовский шум, статистически
независимый от полезного сигнала, то h(t) не зависит от выбора вида сигнала и скорость передачи
информации R будет максимальна, если h(U) максимальна. Это
условие выполняется, если полезный сигнал U(t) также будет гауссовским
процессом. При этом скорость передачи информации
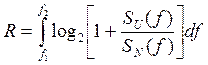
где SU(f), SN(t) – спектральные плотности мощности сигнала и помех (шума) на входе приемного устройства.
Если заданы средняя мощность сигнала PC и спектральная плотность мощности шума SN(f) на входе приемного устройства, то скорость передачи будет зависеть только от распределения мощности полезного сигнала по частоте, т.е. от вида функции SU(f). Максимальная скорость передачи (пропускная способность) достигается при выполнении условия
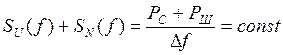
где
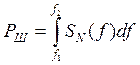 -
средняя мощность шума.
-
средняя мощность шума.
При этом
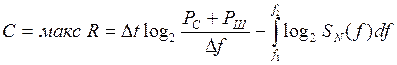 бит/с.
бит/с.
Физический смысл поясняется с помощью рисунка, на котором изображены примерные графики спектральных плотностей сигнала и помехи. Для достижения максимальной скорости передачи информации спектральная плотность сигнала (на рисунке заштрихована) должна быть такой, чтобы основная часть мощности сигнала была сосредоточена в той области спектра, где мала спектральная плотность помехи.
Анализ
уравнения позволяет установить, что при фиксированных значениях средних
мощностей сигнала и шума неименьшую пропускную способность имеет канал, в
котором действует гауссовский шум с постоянной спектральной плотностью N0 в полосе ![]() канала.
Такая помеха образуется при действии на входе приемника белого гауссовского
шума. Из этого следует, что белый гауссовский шум обладает наибольшим мешающим
действием.
канала.
Такая помеха образуется при действии на входе приемника белого гауссовского
шума. Из этого следует, что белый гауссовский шум обладает наибольшим мешающим
действием.
Подставляя в предыдущую формулу значение ![]() и учитывая, что
и учитывая, что ![]() , получаем
формулу Шеннона для канала с белым гауссовским шумом (такой канал обычно
называется гауссовским)
, получаем
формулу Шеннона для канала с белым гауссовским шумом (такой канал обычно
называется гауссовским)
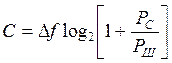
Сигналы, помехи и каналы часто определяют характеристикой, называемой физическим объемом. Под физическим объемом понимают произведение трех его физических характеристик: Tc – длительность сигнала, Fc – ширина спектра частот сигнала
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.