Определение интервалов дискретизации одиночного прямоугольного импульса

Практическое занятие №4

Определение интервалов дискретизации одиночного прямоугольного импульса

Цель работы: Выбрать интервал дискретизации и определить число отсчетов для полного описания одиночного прямоугольного импульса.

Краткие сведения из теории

Важное значение в теории передачи сигналов имеет пространство сигналов с финитным спектром, т.е таких сигналов  с интегрируем квадратом, для которых преобразование Фурье  при . Ортогональный (не нормированный) базис в пространстве функций с финитным спектром:

,

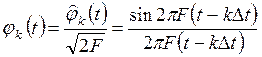где ;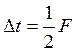

Функции  называются функциями отсчета. При , где  - любое целое положительное или отрицательное число, все функции отсчета, кроме , равны 0, а .

Любую функцию  с финитным спектром можно представить рядом , называемым рядом Котельникова.

Коэффициенты ряда Котельникова представляют собой значения (отсчеты) функции , взятые в моменты времени, кратные .

Теорема Котельникова:

Сигнал с финитным спектром можно точно восстановить по его отсчетам, взятым через интервалы времени 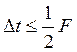, где  - верхняя частота спектра сигнала.

Ход работы:

Вариант №1.

Исходные данные:

В.

.

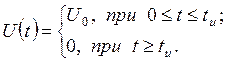
Рисунок №6. График зависимости .

Построим график функции  и определим частоту .

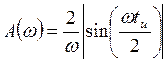
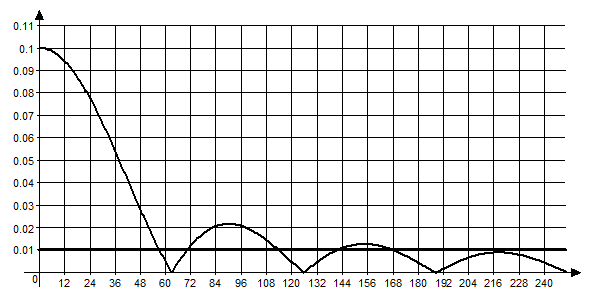
Рисунок 7. График зависимости .

 кГц.

Рассчитаем .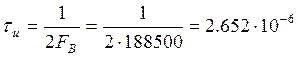

Количество независимых выборок, необходимых для полного восстановления сигнала: .

Выводы: В практической работе выбран интервал дискретизации и определено число отсчетов для полного описания одиночного прямоугольного импульса

20.03.2005 г.                                                        __________________