Другие предметы \ Теория передачи сигналов

Оценка помехоустойчивости стандартного частотного демодулятора

Страницы работы

6 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Содержание работы

Белорусский государственный университет транспорта

Кафедра «Системы передачи информации»

ОТЧЁТ

ПО ПРАКТИЧЕСКОМУ ЗАНЯТИЮ №5

на тему:

Оценка помехоустойчивости стандартного частотного демодулятора

Вариант №17

Выполнил:

ст. гр. ЭС-31

Матылицкий И. В.

Проверил:

Ст. преподаватель

Кушнерова Ю. А.

Гомель 2007

Практическое занятие №5

Оценка помехоустойчивости стандартного частотного демодулятора

Цель работы:

1. Рассчитать суммарную приведенную погрешность СПИ с ЧМ.

2. Найти и рассчитать пороговое отношение "сигнал-шум" для демодулятора.

3. Построить графики кривых помехоустойчивости в зависимости от приведенной суммарной погрешности при Мчмп=const.

>	restart:

Исходные данные:
N-номер по журналу;

>	N:=17:

>	M_fmp_1:=evalf(4+0.2N): M_fmp_2:=evalf(2M_fmp_1): a:=2:

Решение

- пиковый индекс ЧМ.

- отношение мощности сигнала к мощности шума на входе приемного устройства.

- нормированная (приведенная) погрешность.

- приведенная суммарная погрешность (отношение мощности сигнала к суммарной мощности шума на входе приемного устройства).

- аномальная погрешность.

Задаем расчетные значения нормированной погрешности

= 0.00001, 10..130

>	alphaList:=[0.00001,10,20,30,40,50,60,70,80, 90,100,110,120,130]:

Задаем функции искомых погрешностей

sigma_s_1:=(i)->evalf((1.67/(M_fmp_1^2*alphaList[i])

+20*(M_fmp_1+1)/(M_fmp_1^2)*exp(-alphaList[i]

/(M_fmp_1+1)))):
sigma_s_2:=(i)->evalf((1.67/(M_fmp_2^2*alphaList[i])

+20*(M_fmp_2+1)

/(M_fmp_2^2)*exp(-alphaList[i]/(M_fmp_2+1)))):
sigma_H_1:=(i)->evalf((1.67/(M_fmp_1^2

*alphaList[i]))):
sigma_H_2:=(i)->evalf((1.67/(M_fmp_2^2

*alphaList[i]))):
sigma_an_1:=(i)->evalf((20*(M_fmp_1+1)/M_fmp_1^2

*exp(-alphaList[i]/(M_fmp_1+1)))):
sigma_an_2:=(i)->evalf((20*(M_fmp_2+1)/M_fmp_2^2

*exp(-alphaList[i]/(M_fmp_2+1)))):

Определяем искомые погрешности относительно переменной отношения сигнал-шум первого значения Мчмп:

>	sigma_s_1M:=eval(Vector(14,sigma_s_1)): sigma_H_1M:=eval(Vector(14,sigma_H_1)): sigma_an_1M:=eval(Vector(14,sigma_an_1)): print(sigma_s_1M); print(sigma_H_1M); print(sigma_an_1M);


0.0001	3052.739222	3049.671293	3.067929146
10	0.9359357283	0.003049671293	0.9328860570
20	0.2851934984	0.001524835646	0.2836686628
30	0.08727351182	0.001016557098	0.08625695472
40	0.02699112478	0.0007624178232	0.02622870696
50	0.008585465871	0.0006099342586	0.007975531612
60	0.002933449737	0.0005082785488	0.002425171188
70	0.001173104728	0.0004356673276	0.000737437400
80	0.000605446244	0.0003812089116	0.000224237333
90	0.000407037654	0.0003388523659	0.000068185288
100	0.000325700668	0.0003049671293	0.000020733539
120	0.000283547425	0.0002772428448	0.000006304580
130	0.000256056348	0.0002541392744	0.000001917074

Определяем искомые погрешности относительно переменной отношения сигнал-шум второго значения Мчмп:

= 0.00001, 20..230

>	alphaList:=[0.00001,20,40,60,80,100,120,140 ,160,180,200,220,230]: sigma_s_2M:=eval(Vector(13,sigma_s_2)): sigma_H_2M:=eval(Vector(13,sigma_H_2)): sigma_an_2M:=eval(Vector(13,sigma_an_2)): print(sigma_s_2M); print(sigma_H_2M); print(sigma_an_2M);


0.00001	763.8604812	762.4178232	1.442657962
20	0.4072213547	0.000381208911	0.4068401458
40	0.1149224424	0.000190604455	0.1147318379
60	0.0324822705	0.000127069637	0.03235520088
80	0.0092197008	0.0000953022279	0.009124398614
100	0.00264938760	0.0000762417823	0.002573145826
120	0.000789180389	0.0000635348186	0.0007256455706
140	0.000259095669	0.0000544584159	0.0002046372534
160	0.000105360286	0.0000476511139	0.0000577091725
180	0.0000586309462	0.0000423565457	0.0000162744004
200	0.0000427103887	0.0000381208911	0.0000045894975
220	0.0000359496268	0.0000346553556	0.0000012942712

Определяем пороговые значения отношения сигнал-шум:

= 0..230, =78, =182

Графики приведенной суммарной погрешности:

>	alphaList:='alphaList': alphaList[i]:='alpha_H':

>	plot([sqrt(sigma_s_1(i)),sqrt(sigma_s_2(i))],alpha_H=0..230,y=0..0.1);

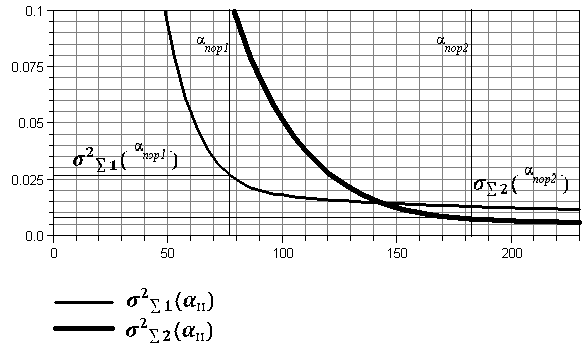
Вывод: Рассчитали суммарную приведенную погрешность СПИ с ЧМ, пороговое отношение "сигнал-шум" для демодулятора. Построили графики кривых помехоустойчивости в зависимости от приведенной суммарной погрешности при Mчмп=const. Чем выше индекс модуляции тем больше значение порогового отношения сигнал-шум

18.05.2007 _________________

Информация о работе

ВУЗ:

Белорусский государственный университет транспорта (БелГУТ)

Предмет:

Теория передачи сигналов

Тип:

Отчеты по лабораторным работам

Категория:

Другие предметы (Технические предметы)

Размер файла:

40 Kb

Скачали:

Скачать файл

Оценка помехоустойчивости стандартного частотного демодулятора

Страницы работы

Содержание работы

Похожие материалы

Информация о работе