Законы управления для регулирующих устройств

                                           Законы управления для регулирующих

                                                                    устройств.

      Для регулирующих устройств (регуляторов) характерным является использование как простых законов регулирования, к которым относятся пропорциональный, интегральный и дифференциальный законы управления, так и сложных регуляторов, реализующих пропорциональный - интегральный закон управления и интегрально-пропорционально-дифференциальный  закон  сразличными сочетаниями коэффициентов  этих законов.

       Характеристики регулирования устройств анализируются на примере реакции таких устройств на ступенчатое  единичное воздействие, или гармоническое синусоидальное воздействие или воздействие в виде коротких импульсов постоянной амплитуды.

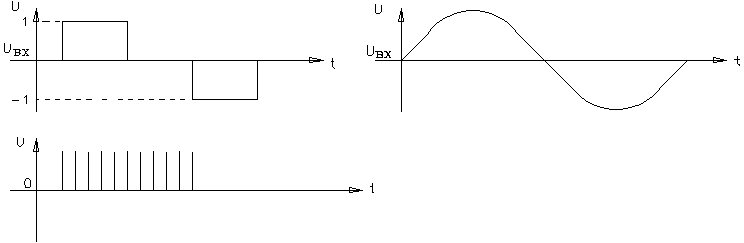
                                         1. Пропорциональный закон управления.

     Наиболее просто этот закон реализуется на безинерционном усилительном звене, которое в  общем случае является обычным ОУ, с коэффициентом усиления, определяемым отношением сопротивлений в цепи О.С. и во входной цепи.

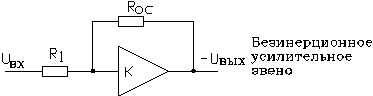
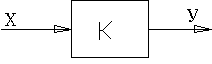
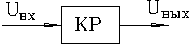
                              Структурная схема САР реализующей пропорциональный закон

                                                  управления будет иметь следующий вид

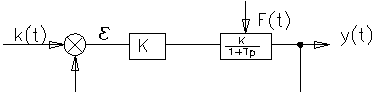
       С точки зрения автоматического управления большинство объектов регулирования представляют собой апериодические звенья 1 порядка с передаточной функцией

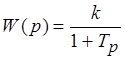
    Примерами таких регулирующих звеньев являются усилители разного рода, потенциометры , рычажные и зубчатые передачи и т.д.

    Выделим регулятор , подаем на вход регулирующие воздействия в виде единичного ступенчатого воздействия

     Уравнения этого РУ будет иметь вид      .

                                                    Обозначим

  Тогда выражение передаточной функции РУ

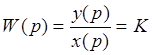
                           Реакция регулирующего устройства может быть

                                       представлено в следующем виде

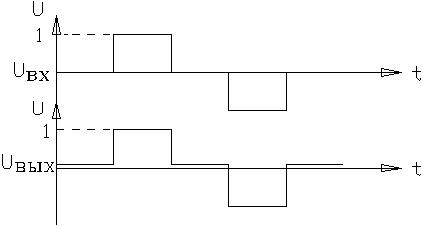
Хотя   K   называется коэффициентом усиления, но на практике  К  может быть больше и меньше  1.   Поскольку отсутствует сдвиг по времени между входным и выходным сигналами этот коэффициент показывает соотношение между    .   Такие регуляторы имеют большое  быстродействие.   Обозначают   эти РУ как П- регулятор  или  пропорционатор.

    Характерная особенность  П-регулятора - наличие сигнала рассогласования для управляющего воздействия

         Вследствии этого возникает противоречие между погрешностью ррегулирования  e , коэффициентом усиления К и  устойчивостью системы автоматического регулирования.

     Системы с  П- регуляторами всегда имеют погрешность регулирования и зону нечувствительности.

                                            2. Дифференциальный закон управления.

        Структурная схема САР с дифференциальным законом управления будет иметь вид

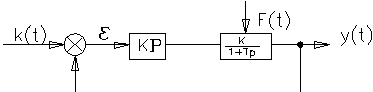
           Операторное уравнение этого РУ, выражение передаточной функции и представление РУ в виде динамического звена показано ниже

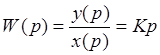
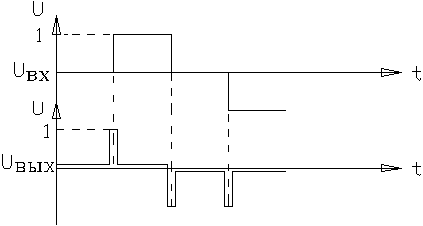
      Реакция РУ с дифференциальным законом управления на ступенчатое единичное воздейстие будет иметь вид

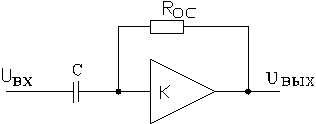
    Дифференцирующее регулирующее устройство может быть построено на  OY  с конденсатором на входе и сопротивлением в цепи  ОС. 

В момент скачка входного сигнала напряжения на выходе идеального Д-регулятора стремится к ¥, а затем  к  0.   В реальных схемах   не достигает  ¥ из-за паразитной постоянной времени и внутреннего сопротивления источника питания .

     В реальной схеме имеет место скачок   до некоторого значения, а затем возврат к 0.

     Примерами  Д-регуляторов является  устройство впрыска топлива в двигателях, регуляторы для управляемых взрывных устройств и т.д.  Необходимость использования Д-регуляторов возникает сравнительно редко, что объясняется тем , что взаимодействующие с регуляторами тиристорные и транзисторные преобразователи характеризуются высоким быстродействием и возникающие в них искажения напряжений и токов могут внести через диф. цепь возмущение в схему регулирования.

                                                 3. Интегральный закон управления.

    Структурная схема САР с интегральным законом управления

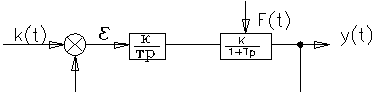
  РУ в виде динамического звена, построение этого РУ на операционном усилителе, а также операторное уравнение и передаточная функция будет иметь вид

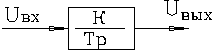
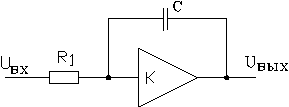
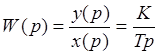
  Характерной особенностью И-регулятора является то, что его   изменяется линейно в течение всего времени , пока на его вход подается напряжение отличное от 0.  При скачкообразном изменении   ,  начнет линейно расти от 0. Через промежуток времени ,  равный постоянной интегрирования t, напряжение на выходе станет равным MAX.