Диспетчеризация с помощью периодической последовательности

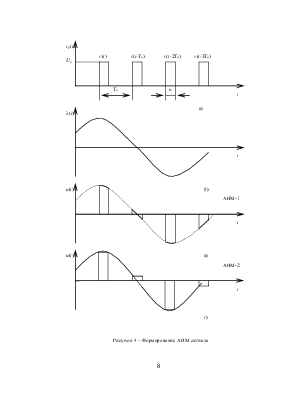
1.2.1. При АИМ – 1 (еще называемый в зарубежной литературе естественной выборкой) диспетчеризация осуществляется с помощью периодической последовательности v_т(t) импульсов прямоугольной формы v(t), следующих с периодом Т_о (рисунок 4,а):

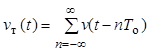                                                  ,                                             (4)

Модулированный сигнал (АИМ-1) получается в результате перемножения непрерывного информационного сигнала l(t) и сигнала – переносчика v_т(t):

                                                      ,                                                     

На рисунках 4,б,в соответственно показаны исходный информационный сигнал l(t) и модулированная последовательность импульсов u(t) на выходе модулятора.

Из рисунка 4,в видно, что в пределах длительности импульсов амплитуда выходного сигнала повторяет изменение входного сигнала, а в остальные моменты времени равна нулю. В этом случае АИМ – 1 модулятор фактически представляет собой ключ, который пропускает или, соответственно, не пропускает в определенные промежутки времени информационный сигнал со входа на выход.

Найдем спектр АИМ – 1 сигнала. Поскольку импульсный сигнал u(t) на выходе модулятора есть произведение двух сигналов (информационного l(t) и сигнала – переносчика v_т(t)), то по теореме о свертке его спектр U(w) получается сверткой спектра информационного сигнала L(w) и спектра сигнала – переносчика V_т(w):

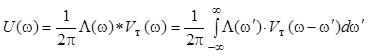                       .                  (5)

Спектр информационного сигнала по определению есть

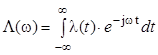
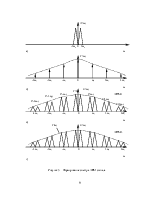
и показан на рисунке 5,а для частного случая речевого сообщения, ограниченного частотой w_В.

Спектр периодической последовательности прямоугольных импульсов выражается формулой

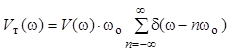                                        .                                   (6)

Здесь w_о=2p/Т_о частота первой гармоники спектра последовательности прямоугольных импульсов (равная частоте следования импульсов, т. е. частоте дискретизации). В приведенной формуле функция

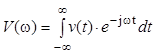
является спектром одиночного импульса.

Кроме того, в формуле (6) в качестве функции V(w) может быть использовано выражение

                                             ,                                            

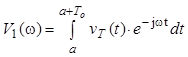представляющие собой спектр периодической последовательности, вычисляемой за один период, и с точностью до множителя 1/Т_о совпадающий с комплексными амплитудами дискретного ряда Фурье, т. е. A_n=V₁(nw_o)/T_o. В последнем интеграле а – произвольное число, определяющее начало интегрирования и выбираемое исключительно из соображений простоты расчетов. Следует отметить, что функция V(w) и V₁(w), вообще говоря, различны и совпадают лишь в точках, кратных w_o. Поскольку спектр V_т(w) отличен от нуля только в указанных точках, то это обстоятельство и позволяет использовать любую из двух функций V(w) или V₁(w).

Таким образом, спектр сигнала – переносчика V_т(w) представляет собой набор равностоящих друг от друга дельта – функций, изображаемых вертикальными стрелками (рисунок 5,б), амплитуды которых изменяются в соответствии со спектральной характеристикой одиночного импульса, являющейся фактически огибающей этих дельта – функций.

После выполнения свертки с учетом стробирующего свойства дельта – функции

                                             ,                                            

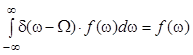где f(w) есть произвольная непрерывная функция, а W - фиксированное число, окончательно для спектра АИМ – 1 сигнала получим выражение

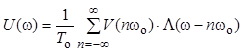                                      .                                 (7)

Правая часть полученной формулы представляет собой спектр информационного сигнала L(w), повторяющийся через w_о, причем амплитудные коэффициенты изменяются как выборки из спектра одиночного импульса V(nw_о).

Таким образом, искомый АИМ – 1 сигнал является совокупностью равностоящих “картинок” одинаковой формы, но различной амплитуды (рисунок 5,в).

Спектр исходного непрерывного сигнала, поступающего на вход модулятора, представляет собой “нулевую картинку”, расположенную вблизи начала координат. Следовательно, исходный сигнал l(t) можно выделить из импульсного сигнала u(t), используя фильтр нижних частот. Частота среза такого фильтра должна находиться в пределах (см. рисунок 5,в)

                                                        w_в < w_с< w_о-w_в.                                                       

Характерно, что сигнал восстанавливается без понижений, несмотря на то, что выборка неидеальная.

Под неидеальной понимается выборка, осуществляемая с помощью импульсов конечной длительности t_и, в то время как по теореме Котельникова дискретизация идеальная – с помощью импульсов нулевой длительности – нам необходимо знать необходимо знать значения функции в отдельных равностоящих точках. Заметим, что сказанное справедливо для импульсов произвольной длительности, вплоть до случая t_и=Т_о, когда импульсы сливаются в сплошной сигнал.