Изучение принципов построения и исследование корректирующих свойств циклических кодов

Белорусский государственный университет транспорта

Кафедра «Системы передачи информации»

Отчет.

По практическому занятию по дисциплине

«Теория передачи сигналов»

            Выполнил:                                                 Проверил:

            студент группы ЭТ-31                              доцент

            Руцкий П.П.                                               Бурченков В.В.

Гомель 2004г.

Методика выполнения работы:

2.1 Кодирование циклическим кодом

2.2 Вывод о проделанной работе.

3.Исходные данные для расчётов

Используем двоичный ко 8421.

14₁₀=1110₂

4.Результат расчётов.

Кодовая комбинация А(х)=х³+х²+х=1110;   r=4

q(x)=x³+x²+x+1

Найдём остаток R(x):

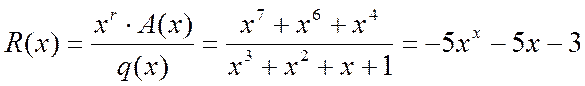Закодированная кодовая комбинация запушиться следующим образом

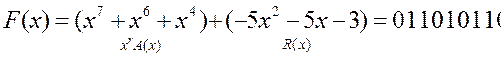
5. Вывод:

В данном практическом задании мы закодировали число циклическим кодом. Из практического задания мы видим что эти коды обладают высоким корректирующим свойством.

15.04.2004.                                                 _____________________

Практическое занятие №8.

ИССЛЕДОВАНИЕ ЦИКЛИЧЕСКИХ КОДОВ

Цель работы: изучить принципы построения циклических (n, k) кодов. Исследовать корректирующие свойства циклических кодов.

1. Краткие сведения из теории.

Циклические коды являются разновидностью систематических кодов и обладают всеми их свойствами. На практике обнаружились высокие корректирующие свойства этих кодов. Упрощение кодирующих и декодирующих устройств достигается за счет наложения дополнительных ограничений на подгруппу разрешающих кодовых комбинаций циклического кода. В коде на подгруппу разрешенных кодовых комбинаций, помимо условия замкнутости по отношению к операции сложения, накладываются также ограничения по отношению к операции умножения (циклического сдвига элементов кодовых комбинаций на одну позицию вправо или влево).

При построении циклических кодов кодовые комбинации принято представлять в виде многочленов переменной  x.

где –коэффициенты, принимающие значения 0 или 1.

Основное свойство рассматриваемых кодов состоит в том, что циклический сдвиг разрешенной кодовой комбинации также является разрешенной кодовой комбинацией. Циклический сдвиг эквивалентен умножению на x кодовой комбинации, записанной в виде многочлена:

Принцип построения комбинации циклических кодов заключается в следующем. Умножим каждую кодовую комбинацию A(x) простого К- элементного кода на x^r, где r=n-k, а затем разделим на порождающий (образующий) многочлен q(x) степени r. В результате умножения A(x) на x^r степень каждого слагаемого x_i, входящего в многочлен A(x), повышается на r. При делении произведения x^r A(x) на q(x) получим частное Q(x) той же степени, что и A(x). Если произведение x^r A(x) не делится нацело на q(x), то получим остаток R(x):

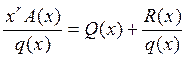
Поскольку частное Q(x) имеет ту же степень, что и A(x), то оно также является комбинацией простого К- элементного кода. Умножая обе части равенства на q(x), после переноса влево произведения Q(x)q(x) получим:

Таким образом, кодовая комбинация циклического кода может быть получена двумя способами:

1)  Неразделимый код–умножение К- элементной комбинации простого кода на образующий многочлен q(x).

2)  Разделимый код – умножение кодовой комбинации простого кода на одночлен x^r и добавлением к этому произведению остатка от деления произведения x^r A(x) на q(x).

На практике в силу простоты чаще используют второй способ.

В соответствии с принципом построения циклического кода в основе схем кодирования и декодирования лежат регистры сдвига, выполняющие операции умножения и деления многочленов. Могут быть созданы устройства на следующие виды порождающих многочленов:

.

Структурная схема кодирующего устройства с порождающим многочленом вида  представлена на рисунке.

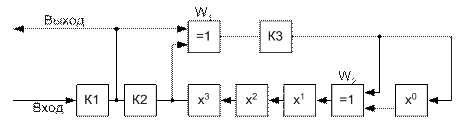
Из схемы видно, что в состав кодера входят r- элементный регистр сдвига, три ключа и двухвходовые сумматоры по модулю 2, причем их число на единицу меньше числа ненулевых членов образующего многочлена q(x). Структура логических обратных связей в регистре сдвига, число элементов которого равно степени образующего многочлена, полностью определяется видом порождающего многочлена.

Сумматоры w₁…w_n-1 присутствуют в схеме в том случае, если соответствующие коэффициенты образующего многочлена a₁…a_n-1 равны 1.

Схема кодирующего устройства циклического кода работает следующим образом. Сначала ключ К2 закрыт, а ключи К1 и К3 открыты. Информационный многочлен A(x) поступает одновременно на выход кодера (идет умножение на одночлен x^r) и сумматор w₁. в процессе  ее прохождения за К тактовых импульсов в ячейках регистра сдвига накапливается r проверочных элементов (осуществляется деление x^r A(x) на образующий  многочлен q(x)). После К- ого тактового импульса ключи К1 и К3 закрываются, а ключ К2 открывается. Далее полученные проверочные элементы r тактовыми импульсами поступают на выход кодера.