Диспетчеризация с помощью периодической последовательности, страница 2

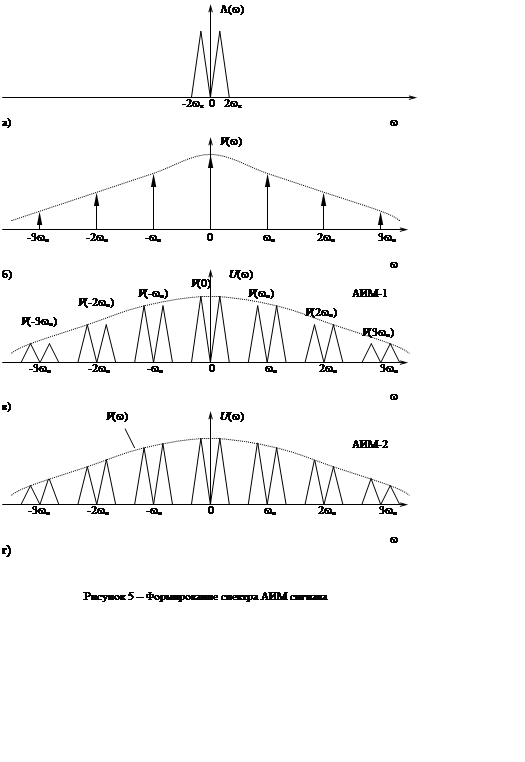
Для передачи сигнала при идеальной выборке требуется бесконечно большая полоса частот, поскольку огибающая V(w) спектра (см. рисунок 5,в) в этом случае является постоянной функцией и спектр увеличения частоты не убывает.

При выборке огибающая V(w) является убывающей функцией частоты. По мере увеличения ширины импульсов спектр убывает быстрее и, следовательно, для передачи требуется меньшая полоса частот. Однако то, что выигрывается в частотной области, проигрывается во временной. При увеличении ширины импульсов уменьшается свободный промежуток времени Т_о-Т_и, когда система простаивает и может быть использована для передачи других АИМ – сигналов (временное уплотнение). Таким образом, при этом уменьшается общее число передаваемых АИМ – сигналов (организуемых каналов связи).

В заключение заметим, что при выводе выражений для спектра нигде не использовалось то обстоятельство, что импульсы имеют прямоугольную форму. Следовательно, полученные формулы справедливы для импульсов любой формы v(t), в частности, импульсы могут даже частично перекрываться. Форма импульсов влияет лишь на вид огибающей спектра V(w) (см. рисунок 5,в).

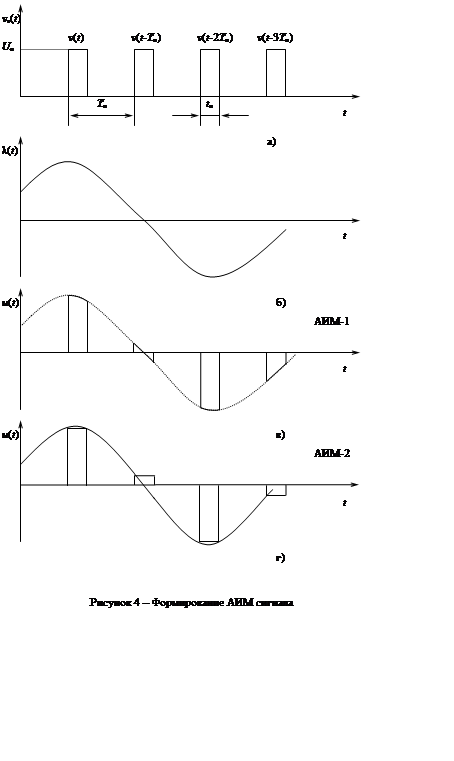
1.2.2. В случае АИМ – 2 сигнала (в зарубежной литературе данный вид модуляции известен как мгновенная выборка) все импульсы имеют одну и ту же форму, а их амплитуды пропорциональны значениям соответствующих отсчетов (рисунок 4,г). очевидно, такой импульсный сигнал несет полную информацию, содержащуюся во всех отсчетах, и, следовательно, в соответствии с теоремой Котельникова информацию, относящуюся к непрерывному информационному сигналу l(t).

Таким образом, ни одна из “картинок” на рисунке 5,г не имеет формы “нулевой картинки” L(w). Кроме того, данный вывод непосредственно следует из формул (7) и (9). В формуле (7) множитель V(nw_o) постоянен для данного n, тогда как в формуле (9) множитель V(w) является функцией частоты.

Рассмотрим теперь вопрос о восстановлении исходного сигнала.

Если пропустить АИМ – 2 сигнал через фильтр нижних частот, то спектр выходного сигнала будет  и, следовательно, сам сигнал будет отличаться от требуемого. Неискаженный сигнал l(t) можно получить из этого выходного напряжения, пропустив его через другой фильтр, который имеет передаточную характеристику 1/V(w). Поскольку спектр исходного сигнала L(w) ограничен частотой w_В, то достаточно, чтобы второй фильтр имел указанную передаточную функцию только в пределах |w|=w_в. Вне этой полосы передаточная функция может выбираться произвольно в зависимости от удобства реализации. Оба фильтра можно объединить в один составной фильтр. Очевидно, передаточная функция такого фильтра

                                                .                                               

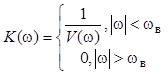Если импульс v(t) является очень узким, то он приближается к дельта – функции, а спектр V(w) стремится к равномерному. Иными словами, функция V(w) почти постоянна в интервале . В таком случае составной фильтр превращается в идеальный фильтр нижних частот с частотой среза w_В и сигнал l(t) восстанавливается точно так же, как и при АИМ – 1.

Таким образом, при уменьшении ширины импульсов различие между двумя видами модуляции АИМ – 1 и АИМ – 2 уменьшается и в пределе они совпадают как между собой, так и с идеальным случаем, когда выборка осуществляется с помощью дельта – функций по теореме Котельникова.

1.2.3. Рассмотрим теперь вопрос о выборе величины частоты дискретизации.

1.2.4. Рассмотрим пример определения спектра. Пусть сигналом – переносчиком является последовательность колокольных импульсов вида

                                                  ,                                                 

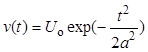где а – коэффициент, равный половине длительности импульса, определяемой по уровню  от максимального значения.

Спектр такого импульса

                                           .                                          

В качестве информационного возьмем периодический сигнал вида

                                                        .                                                       

Для нахождения спектра этого сигнала преобразуем его к сумме гармонических составляющих

                                                   .                                                  

Спектральная характеристика этого сигнала есть

                                .                               

Спектр исходного сигнала, а также сигналов АИМ-1 и АИМ–2 приведены на рисунке 6,а – б соответственно. Подчеркнем различия между спектрами сигналов АИМ-1 и АИМ–2. Амплитуды боковых частот  (верхней) и  (нижней) в спектре АИМ–1 сигнала одинаковы, а в спектре АИМ–2 сигнала различны.

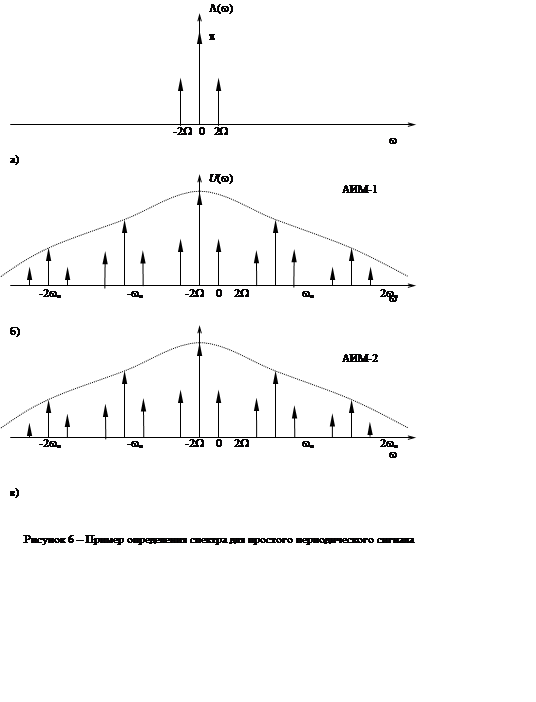Таблица 1