
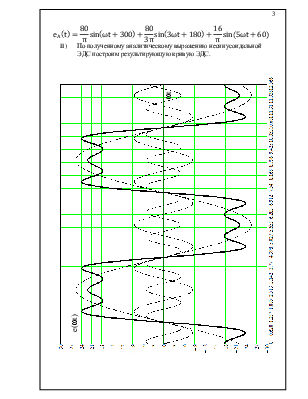









Исходные данные
Параметры ЭДС: Рис.1; А = 20; FI = 300.0; В = 0
Линия: R = 50 Ом; XL = 80 Ом; XC = 40 Ом
Нагрузка 1: R = 0 Ом; XL = 0 Ом; XC = 1500 Ом
Нагрузка 2: R = 80 Ом; XL = 20 Ом; XC = 0 Ом
0–провод: R = 60 Ом; XL = 40 Ом; XC = 0 Ом
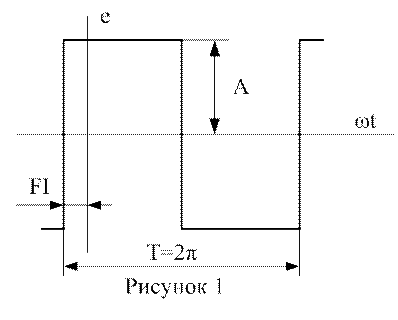
I) Разложим графическую несинусоидальную кривую в ряд Фурье
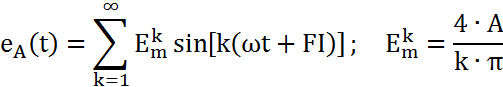
k=1
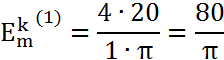
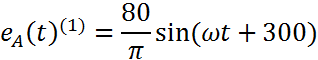
k=3
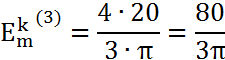
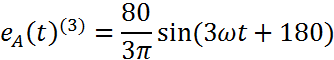
k=5
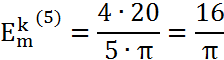
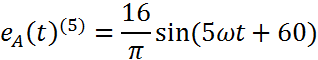
![]()
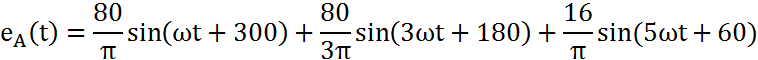
II) По полученному аналитическому выражению несинусоидальной ЭДС построим результирующую кривую ЭДС.
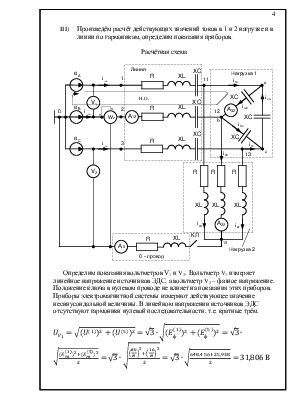
III) Произведём расчёт действующих значений токов в 1 и 2 нагрузке и в линии по гармоникам, определим показания приборов.
Расчётная схема
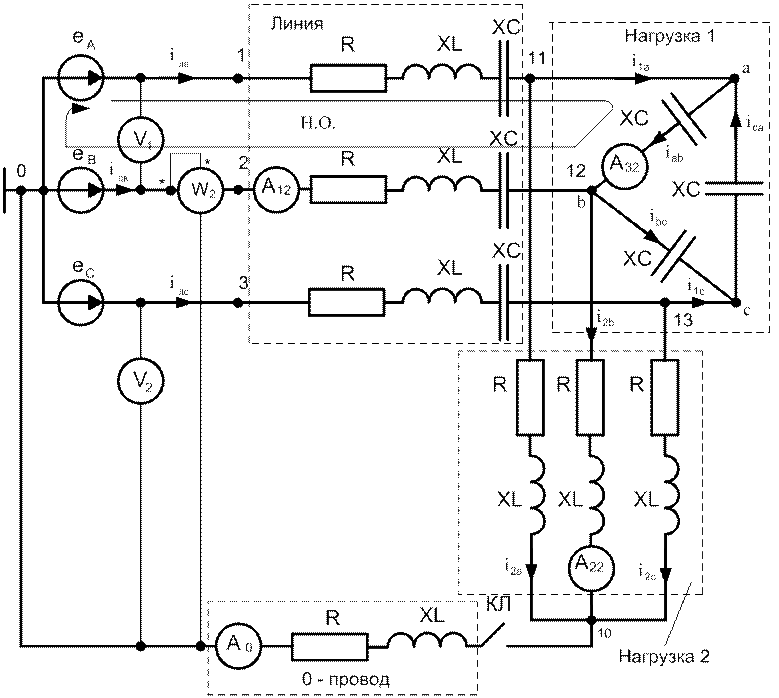
Определим показания вольтметров V1 и V2. Вольтметр V1 измеряет линейное напряжение источников ЭДС, а вольтметр V2 – фазное напряжение. Положение ключа в нулевом проводе не влияет на показания этих приборов. Приборы электромагнитной системы измеряют действующее значение несинусоидальной величины. В линейном напряжении источников ЭДС отсутствуют гармоники нулевой последовательности, т.е. кратные трём.
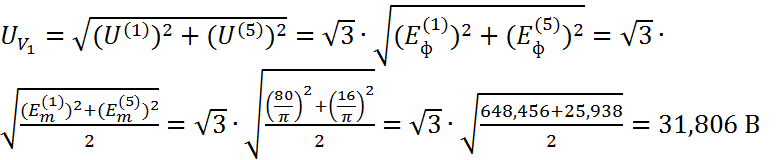
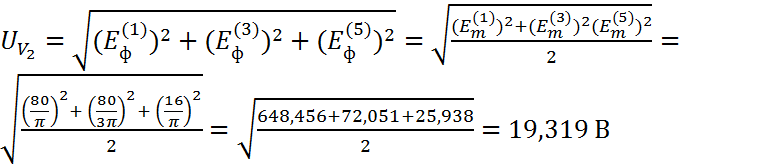
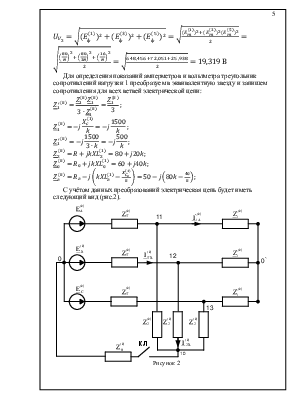
Для определения показаний амперметров и вольтметра треугольник сопротивлений нагрузки 1 преобразуем в эквивалентную звезду и запишем сопротивления для всех ветвей электрической цепи:
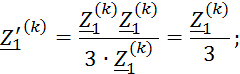

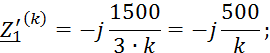
![]()
![]()
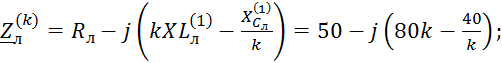
С учётом данных преобразований электрическая цепь будет иметь следующий вид (рис.2).
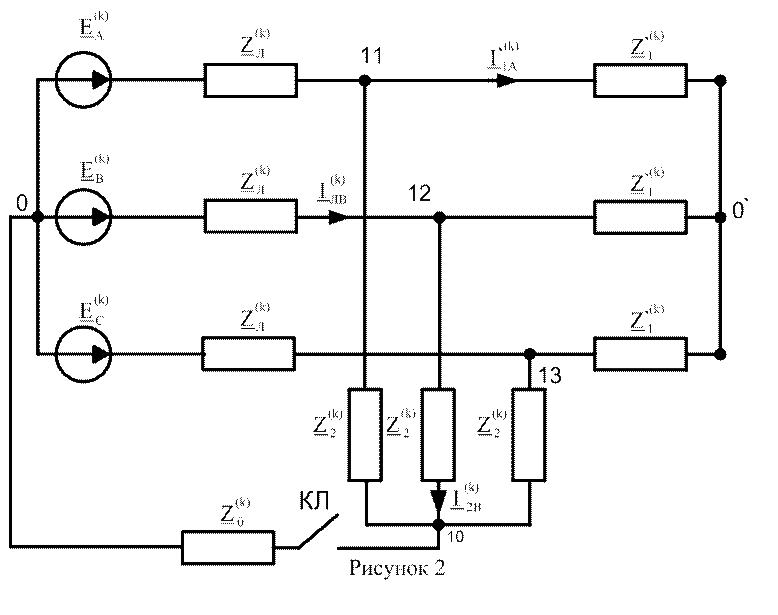
Расчёт цепи без нулевого провода (ключ разомкнут)
В трёхфазной электрической цепи в симметричном режиме система фазных ЭДС третьей гармоники образует нулевую последовательность:
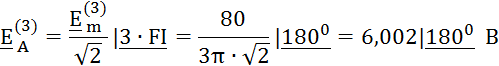
![]()
![]()
Поэтому в трехпроходной трёхфазной электрической цепи без нулевого провода отсутствуют токи третьей гармоники в линейных проводах и нагрузке
![]()
![]()
![]()
![]()
Система ЭДС первой и пятой гармоник представляет собой симметричную систему ЭДС прямой и обратной последовательностей (т.е. EA + EB +EC = 0).
Напряжение смещения нейтрали между точками О – О´ – 10:
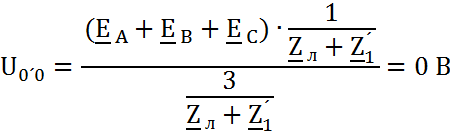
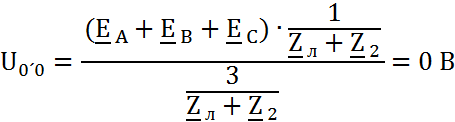
Следовательно, ![]() =
=![]() Это даёт нам право соединить эти узлы
проводами и расчёт вести на одну фазу.
Это даёт нам право соединить эти узлы
проводами и расчёт вести на одну фазу.
Расчёты по первой гармонике
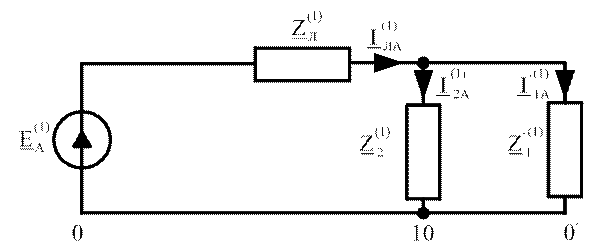
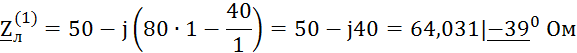
![]()
![]()
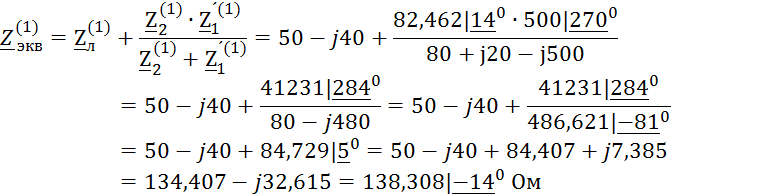
![]()
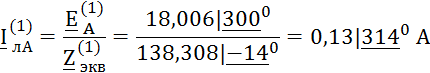
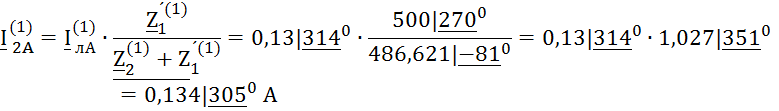
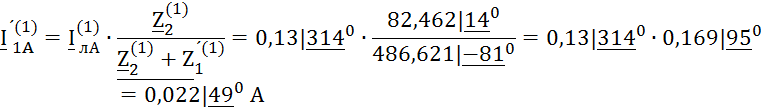
Первая гармоника образует прямую последовательность фаз:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ток ![]() определим по II
закону Кирхгофа для контура на расчётной схеме:
определим по II
закону Кирхгофа для контура на расчётной схеме:
![]()
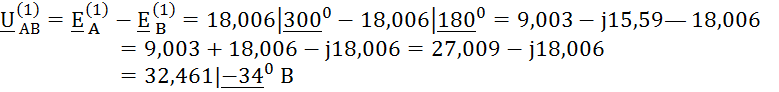
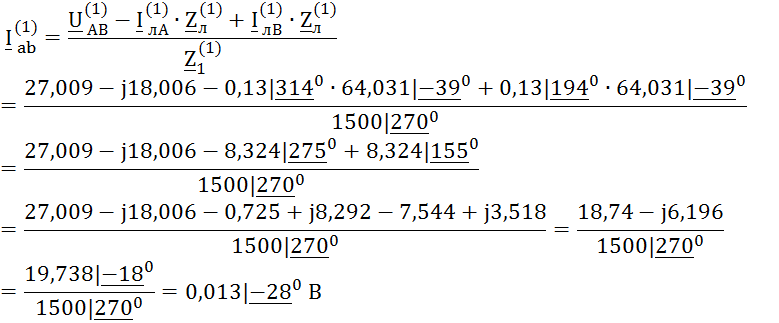
![]()
![]()
![]()
Расчёты по пятой гармонике
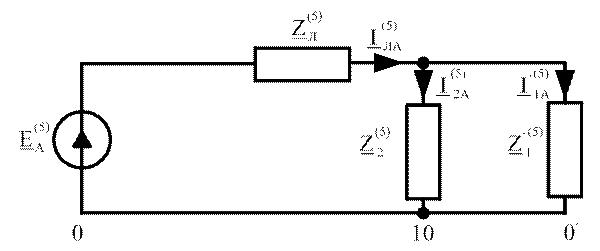
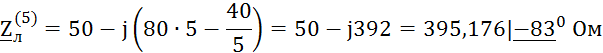
![]()

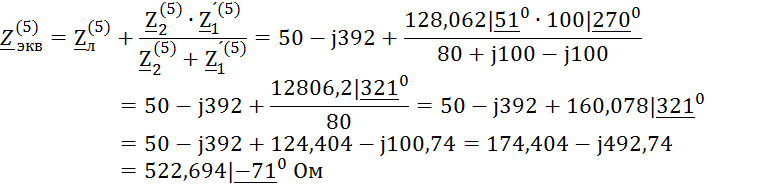
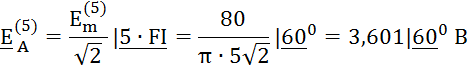
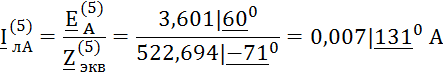
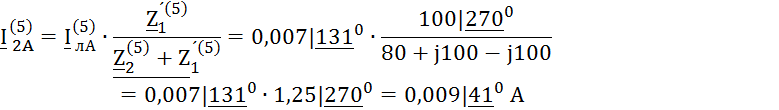
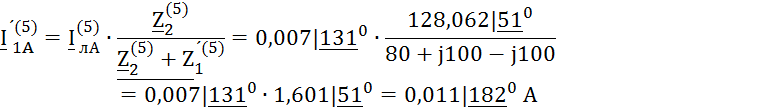
Пятая гармоника образует обратную последовательность фаз:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ток ![]() определим по II
закону Кирхгофа для контура на расчётной схеме:
определим по II
закону Кирхгофа для контура на расчётной схеме:
![]()
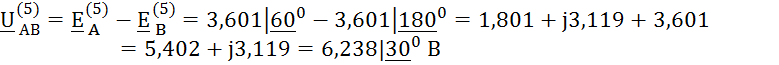
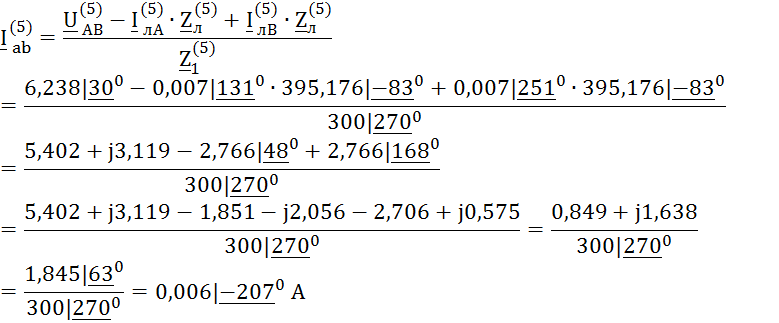
![]()
![]()
![]()
Амперметр А12 показывает действующее значение тока фазы В:
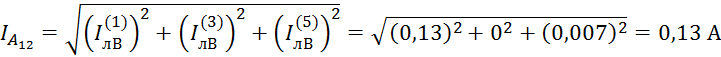
Амперметр А22
показывает действующее значение тока, протекающего по нагрузке
![]() в фазе В:
в фазе В:
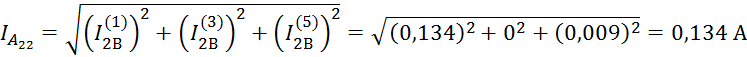
Амперметр А32
показывает действующее значение тока, протекающего по нагрузке ![]() , соединённой треугольником, между узлами а
и b:
, соединённой треугольником, между узлами а
и b:
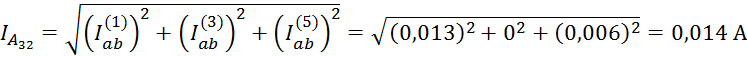
Амперметр А0 показывает действующее значение тока, протекающего в нулевом проводе. Так как ключ разомкнут, ток через амперметр не протекает:
![]() .
.
Ваттметр W2 измеряет активную мощность фазы В:
![]()
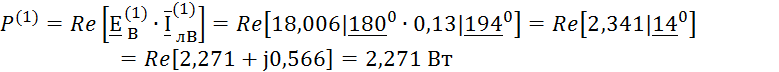
![]()
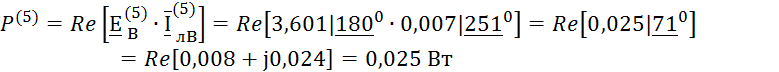
![]()
Найдём напряжение между точками 3 и 12: U3-12
Запишем второй закон Кирхгофа для следующего контура (рис. 3)
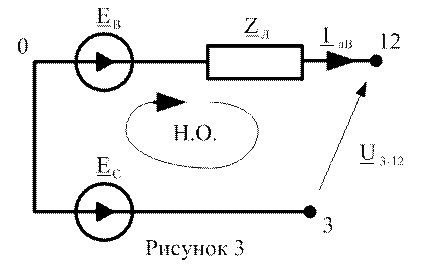
1-я гармоника: ![]()
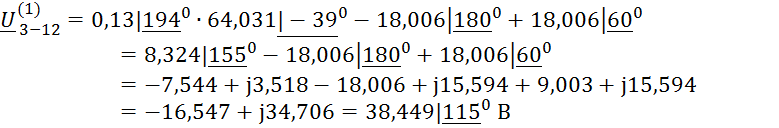
![]() B
B
3-я гармоника: ![]()
![]()
5-я гармоника: 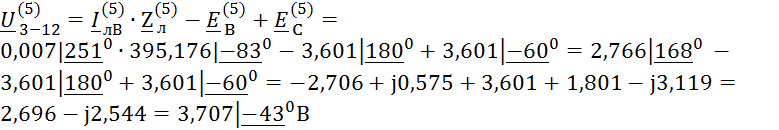
![]() B
B
![]()
Действующее значение напряжения U3-12
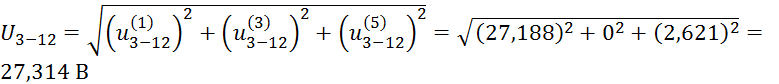
Расчёт цепи с нулевым проводом (ключ замкнут)
Симметричные системы ЭДС прямой и обратной последовательностей в режиме симметричной нагрузки порождают симметричные системы токов.
Их сумма в любой момент времени равна нулю:
![]()
![]()
I закон Кирхгофа для узла 0:
![]()
![]()
Следовательно, ![]() ,
, ![]() .
.
Поэтому для 1-й и
5-й гармоник выполняется равенство ![]() Узлы равных потенциалов соединяем между
собой проводом. В итоге получится схема для расчёта 1-й и 5-й гармоник,
аналогичная схемам для расчёта без нулевого провода. Поэтому токи, протекающие по ветвям, останутся те же, что и в
случае разомкнутого ключа.
Узлы равных потенциалов соединяем между
собой проводом. В итоге получится схема для расчёта 1-й и 5-й гармоник,
аналогичная схемам для расчёта без нулевого провода. Поэтому токи, протекающие по ветвям, останутся те же, что и в
случае разомкнутого ключа.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Расчёты по третьей гармонике
Гармоники, кратные трём, составляют систему нулевой последовательности.
При соединении нагрузки треугольником токов нулевой последовательности в ней нет, следовательно,
![]() ,
, ![]() ,
, ![]() ;
;
![]() ,
, ![]() ,
, ![]() ;
;
По первому закону Кирхгофа для узла 0
![]() ,
,
так как ![]() .
.
По второму закону Кирхгофа для контура 0 – 11 – 10 – 0
![]()
![]()
Для полученного уравнения можно составить эквивалентную схему
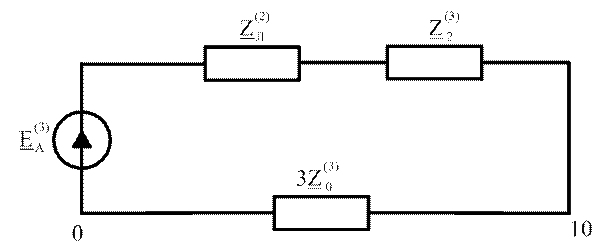
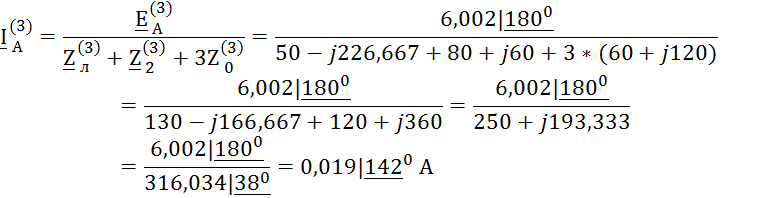
![]()
![]()
![]()
Показания приборов (при замкнутом ключе)
Амперметр А12 показывает действующее значение тока в линии в фазе В:
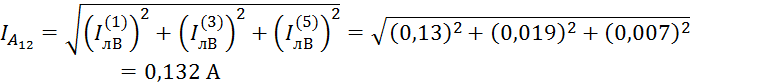
Амперметр А22 показывает действующее значение тока во второй нагрузке фазы В:
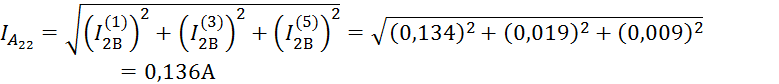
Амперметр А32 показывает действующее значение тока Iab в первой нагрузке между узлами a и b
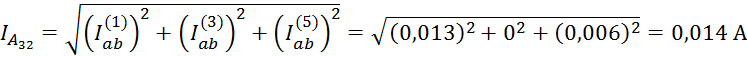
Амперметр А0 показывает действующее значение тока в нулевом проводе
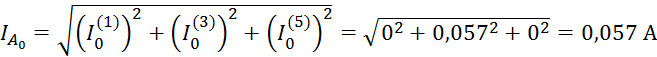
Ваттметр W2 измеряет активную мощность в фазе В:
![]()
![]()
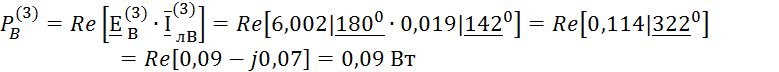
![]()
![]()
Определим напряжение между точками 3 – 12 (U3 – 12). По второму закону Кирхгофа составленного для контура рис.3 для третьей гармоники, получим:
![]()
Напряжение U3 – 12 по первой и пятой гармоникам были определены ранее при расчёте цепи при разомкнутом ключе, при замыкании ключа они не изменились:
![]()
![]()
Действующее напряжение ![]()
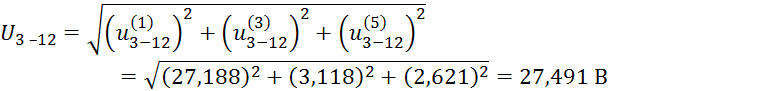
Напряжения U3 – 12 в мгновенной форме при замкнутом ключе:
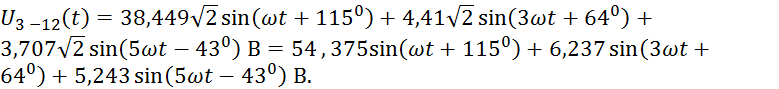
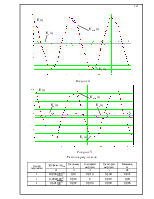
Кривые напряжения U3 – 12(t) при разомкнутом ключе (рис. 4) и при замкнутом ключе (рис. 5).
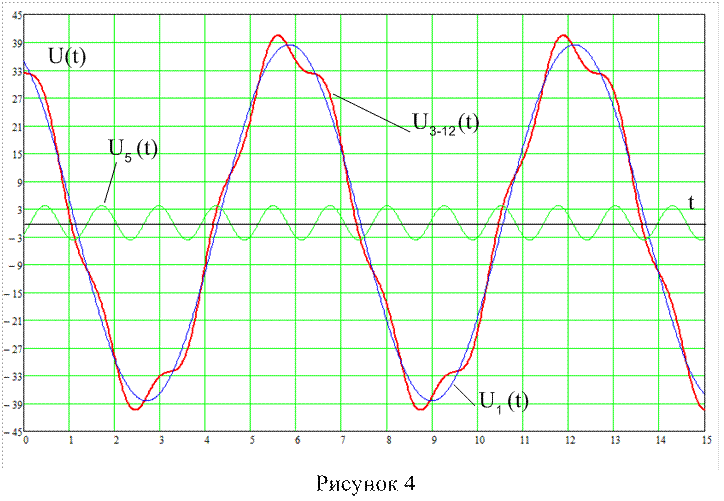
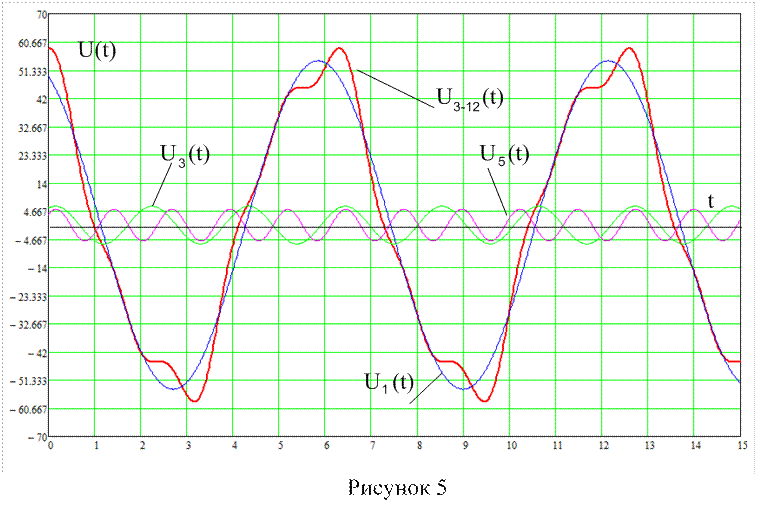
Таблица результатов
|
Номер |
ЭДС фазы А, ЕАm |
Ток линии, Iл |
Ток первой нагрузки |
Ток второй нагрузки |
Мощность, |
||
|
В |
А |
А |
A |
ВТ |
|||
|
1 |
|
|
|
|
|
||
|
3 |
|
|
|
|
|
||
|
5 |
|
|
|
|
|
||
|
Показания прибора |
Uv1 |
Uv2 |
IA12 |
IA32 |
IA22 |
Рw2 |
|
|
Ключ |
|
|
|
|
|
|
|
|
Ключ |
|
|
|
|
|
|
|
|
Ток в нулевом |
Действующее значение
напряжения |
||||||
|
|
Ключ замкнут |
Ключ разомкнут |
|||||
|
|
|
||||||
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.