дробь на простые дроби: 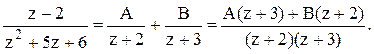 Или
Или ![]() . При z=-2
получим A=-4. Если положить z=-3, то получим В=5.
Следовательно,
. При z=-2
получим A=-4. Если положить z=-3, то получим В=5.
Следовательно, 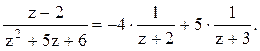 1). В кольце
1). В кольце ![]() имеем
имеем 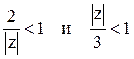 .
Тогда дробь можно представить следующим образом:
.
Тогда дробь можно представить следующим образом: 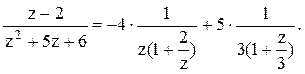 Воспользуемся
формулой для бесконечно убывающей геометрической прогрессии:
Воспользуемся
формулой для бесконечно убывающей геометрической прогрессии: 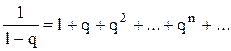 , где
, где ![]() . В
первой дроби q=-2/z, во второй дроби q= -z/3. Следовательно,
. В
первой дроби q=-2/z, во второй дроби q= -z/3. Следовательно, 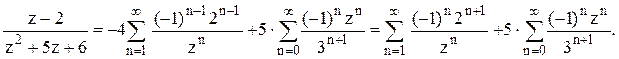 2). В кольце
2). В кольце ![]() выполняются
неравенства
выполняются
неравенства 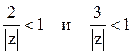 . Следовательно,
. Следовательно, 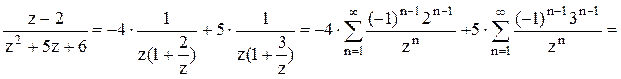
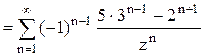 .
.
3) 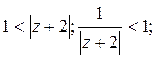
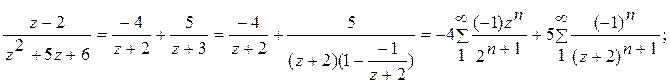
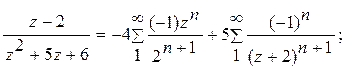
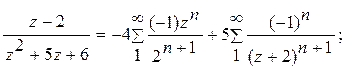
Ответ. 1). 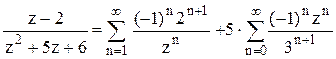 в кольце
в кольце ![]() .
.
2). 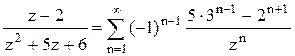 в кольце
в кольце ![]()
3) 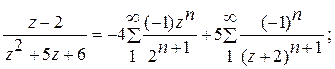 в кольце 1<|z+2|.
в кольце 1<|z+2|.
Задача 9. Разложить функцию в ряд Лорана в областях.
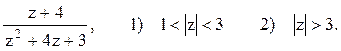 3) 2<|z+3|.
3) 2<|z+3|.
Решение. Корнями уравнения z2+4z+3=0 являются числа z1=-1 и z2=-3. Разложим эту
дробь на простые дроби: 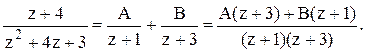 Или
Или ![]() . При z=-1
получим A=3/2. Если положить z=-3, то получим
В=-1/2. Следовательно,
. При z=-1
получим A=3/2. Если положить z=-3, то получим
В=-1/2. Следовательно, 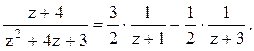 1). В кольце
1). В кольце ![]() имеем
имеем 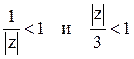 .
Тогда дробь можно представить следующим образом:
.
Тогда дробь можно представить следующим образом: 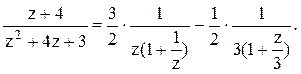 Воспользуемся
формулой для бесконечно убывающей геометрической прогрессии:
Воспользуемся
формулой для бесконечно убывающей геометрической прогрессии: 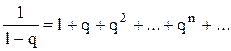 , где
, где ![]() . В
первой дроби q=-1/z, во второй дроби q= -z/3. Следовательно,
. В
первой дроби q=-1/z, во второй дроби q= -z/3. Следовательно, 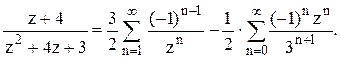 2). В кольце
2). В кольце ![]() выполняются
неравенства
выполняются
неравенства 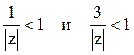 . Следовательно,
. Следовательно, 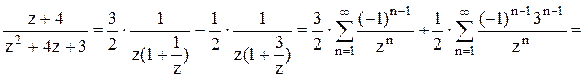
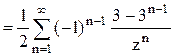 .
.
3) 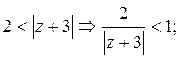
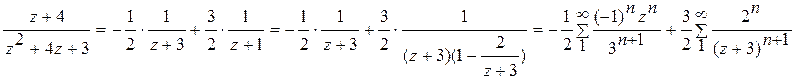
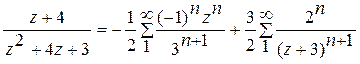
Ответ. 1). 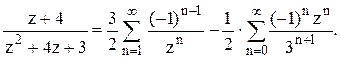 в кольце
в кольце ![]() .
.
2). 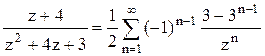 в кольце
в кольце ![]() .
.
3) 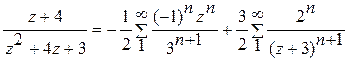 в кольце 2<|z+3|;
в кольце 2<|z+3|;
Задача 9. Разложить функцию в ряд Лорана в областях.
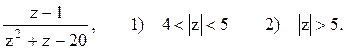 3) 0<|z+5|<9;
3) 0<|z+5|<9;
Решение. Корнями уравнения z2+z-20=0 являются числа z1=4 и z2=-5. Разложим эту
дробь на простые дроби: 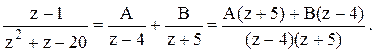 Или
Или ![]() . При z=4
получим A=1/3. Если положить z=-5, то получим
В=2/3. Следовательно,
. При z=4
получим A=1/3. Если положить z=-5, то получим
В=2/3. Следовательно, 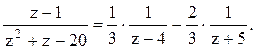 1). В кольце
1). В кольце ![]() имеем
имеем 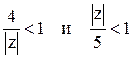 .
Тогда дробь можно представить следующим образом:
.
Тогда дробь можно представить следующим образом: 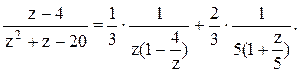 Воспользуемся
формулой для бесконечно убывающей геометрической прогрессии:
Воспользуемся
формулой для бесконечно убывающей геометрической прогрессии: 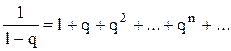 , где
, где ![]() . В
первой дроби q=4/z, во второй дроби q= -z/5. Следовательно,
. В
первой дроби q=4/z, во второй дроби q= -z/5. Следовательно, 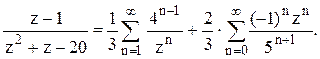 2). В кольце
2). В кольце ![]() выполняются
неравенства
выполняются
неравенства 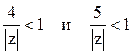 . Следовательно,
. Следовательно, 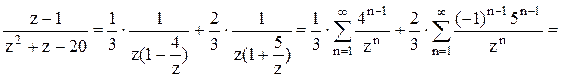
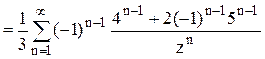 .
.
3) 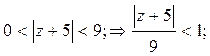
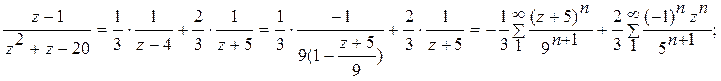
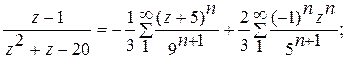
Ответ. 1). 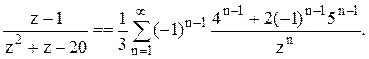 в кольце
в кольце ![]() .
.
2). 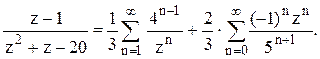 в кольце
в кольце ![]() .
.
3) 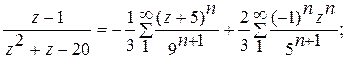 в кольце 0<|z+5|<9.
в кольце 0<|z+5|<9.
Задача 9. Разложить функцию в ряд Лорана в областях.
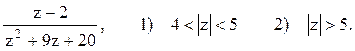 3) 1<|z+5|.
3) 1<|z+5|.
Решение. Корнями уравнения z2+9z+20=0 являются числа z1=-4 и z2=-5. Разложим эту
дробь на простые дроби: 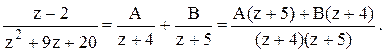 Или
Или ![]() . При z=-4
получим A=-6. Если положить z=-5, то получим
В=7. Следовательно,
. При z=-4
получим A=-6. Если положить z=-5, то получим
В=7. Следовательно, 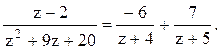 1). В кольце
1). В кольце ![]() имеем
имеем 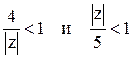 .
Тогда дробь можно представить следующим образом:
.
Тогда дробь можно представить следующим образом: 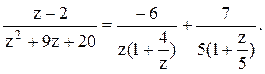 Воспользуемся
формулой для бесконечно убывающей геометрической прогрессии:
Воспользуемся
формулой для бесконечно убывающей геометрической прогрессии: 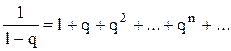 , где
, где ![]() . В
первой дроби q=-4/z, во второй дроби q= -z/5. Следовательно,
. В
первой дроби q=-4/z, во второй дроби q= -z/5. Следовательно, 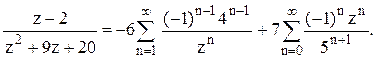 2). В кольце
2). В кольце ![]() выполняются
неравенства
выполняются
неравенства 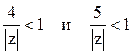 . Следовательно,
. Следовательно, 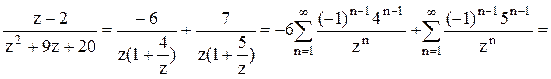
3) 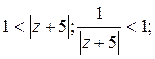
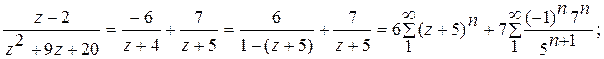
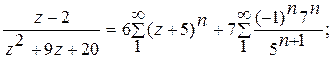
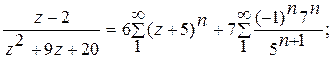
Ответ. 1). 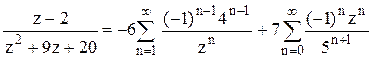 в кольце
в кольце ![]() .
.
2). 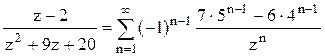 в кольце
в кольце ![]() .
.
3) 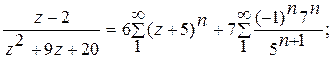 в кольце 1<|z+5|.
в кольце 1<|z+5|.
Задача 9. Разложить функцию в ряд Лорана в областях.
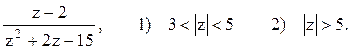
Решение. Корнями уравнения z2+2z-15=0 являются числа z1=3 и z2=-5. Разложим эту
дробь на простые дроби: 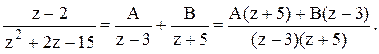 Или
Или ![]() . При z=3
получим A=1/8. Если положить z=-5, то получим В=7/8.
Следовательно,
. При z=3
получим A=1/8. Если положить z=-5, то получим В=7/8.
Следовательно, 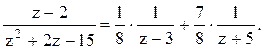 1). В кольце
1). В кольце ![]() имеем
имеем 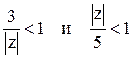 .
Тогда дробь можно представить следующим образом:
.
Тогда дробь можно представить следующим образом: 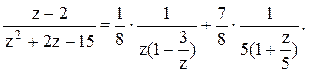 Воспользуемся
формулой для бесконечно убывающей геометрической прогрессии:
Воспользуемся
формулой для бесконечно убывающей геометрической прогрессии: 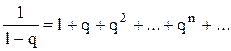 , где
, где ![]() . В
первой дроби q=3/z, во второй дроби q= -z/5. Следовательно,
. В
первой дроби q=3/z, во второй дроби q= -z/5. Следовательно, 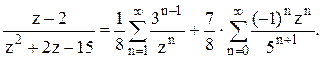 2). В кольце
2). В кольце ![]() выполняются
неравенства
выполняются
неравенства 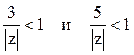 . Следовательно,
. Следовательно, 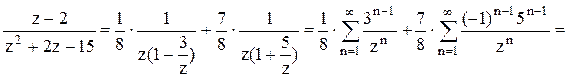
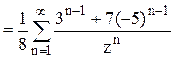 .
.
Ответ. 1). 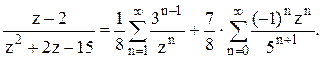 в кольце
в кольце ![]() .
.
2). 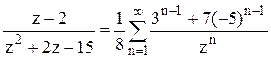 в кольце
в кольце ![]() .
.
Задача 9. Разложить функцию в ряд Лорана в областях.
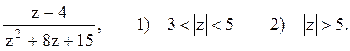
Решение. Корнями уравнения z2+8z+15=0 являются числа z1=-3 и z2=-5. Разложим эту
дробь на простые дроби: 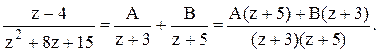 Или
Или ![]() . При z=-3
получим A=-7/2. Если положить z=-5, то получим
. При z=-3
получим A=-7/2. Если положить z=-5, то получим
В=9/2. Следовательно, 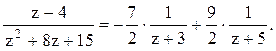 1). В кольце
1). В кольце ![]() имеем
имеем
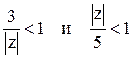 . Тогда дробь можно представить следующим
образом:
. Тогда дробь можно представить следующим
образом: 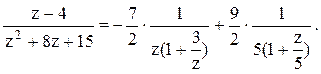 Воспользуемся формулой для бесконечно
убывающей геометрической прогрессии:
Воспользуемся формулой для бесконечно
убывающей геометрической прогрессии: 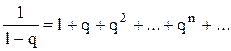 , где
, где ![]() . В первой дроби q=-3/z, во второй дроби q=
-z/5. Следовательно,
. В первой дроби q=-3/z, во второй дроби q=
-z/5. Следовательно, 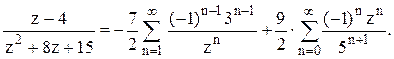 2). В кольце
2). В кольце ![]() выполняются неравенства
выполняются неравенства 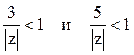 . Следовательно,
. Следовательно, 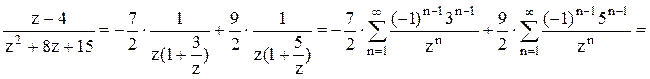
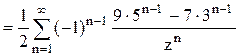 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.