Практический курс теоретических основ электротехники: Методическое руководство (Раздел VIII: Резонанс в электрических цепях)

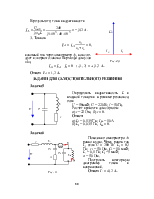
6. Топографическая диаграмма цепи в предположении, что
j _d = 0 (рис. 5,в).

j _b = j _d + I₂Z₂ = 108 Ð 33,7º (B),

j _c = j _d + I₄Z₄ = 36 Ð-146,3º (B),

j _a = j _b + I₁Z₁ = 130 (B).

VIII. РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

Основные вопросы

1.  Какой режим электрической цепи называется резонанс-ным?

2.  Условия резонанса напряжений.

3.  Условия резонанса токов.

4.  Резонансная частота последовательного и параллельного резонансных контуров.

Литература

1.  Зевеке Г.В., Ионкин П.А., Нетушил Л.В., Страхов С.В. Основы теории цепей. – М., 1989. – § 5.1, 5.2, 5.4 ,5.5, 5.7.

2.  Бесонов Л. А. Теоретические основы электротехники. – М., 1978. – § 3…25; 3…29.

Примеры

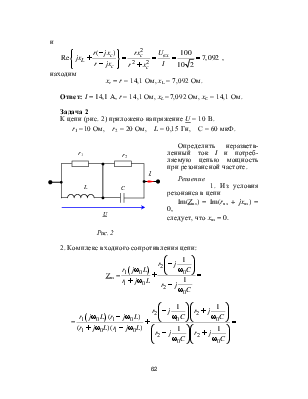
Задача 1

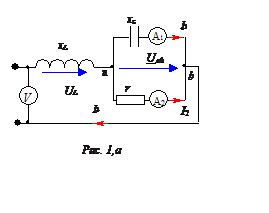Известны показания приборов: амперметры А₁ и А₂ показывают по 10 А, вольтметр на входе цепи показывает 100 В. Входные ток и напряжение совпадают по фазе.

Определить входной ток I и параметры цепи r, x_L, x_C.

Решение

Uab

Вариант 1 (расчет с по-мощью векторной диа-граммы)

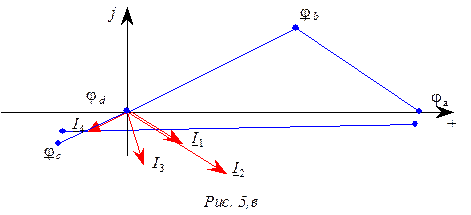
Векторная диаграмма рассматриваемой цепи, пред-ставленная на рис. 1,б, построена в соответствии с

                                                       уравнениями

  и 

при условии совпадения фаз U_вх и I.

Порядок построения векторной диаграммы следующий:

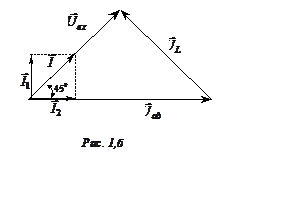· произвольно выби-раем направление вектора ;

· вектор тока  совпадает по направлению с вектором , а вектор тока  опережает его на угол, равный 90°;

·  в силу того, что I₁ =
= I₂, входной ток цепи

,

а изображающий его вектор , опережает напряжение  
на 45°.

Вектор  (длина его выбрана произвольно) суммируется с вектором , опережающим вектор общего тока  на 90°, так, чтобы вектор входного напряжения  совпал с направлением вектора тока .

Из диаграммы следует:

U_L = U = 100 B;

U_ав =  = 100  B;

х_c =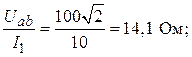

r = х_c = 14,1 Ом;

х_L =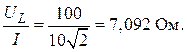

Вариант 2

1. Из условия резонанса

Im(Z_вх) = 0,

где

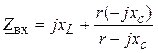
следует, что

.

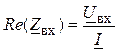2. Из условия I₁ = I₂  вытекает, что

r = х_c  и   (cм. рис. 1,б).

3. Решая совместно уравнения

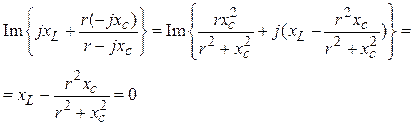
и

,

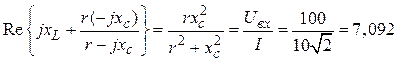находим

x_c  = r = 14,1 Ом, x_L = 7,092 Ом.

Ответ: I = 14,1 A, r = 14,1 Ом, x_L =7,092 Ом, x_C = 14,1 Ом.

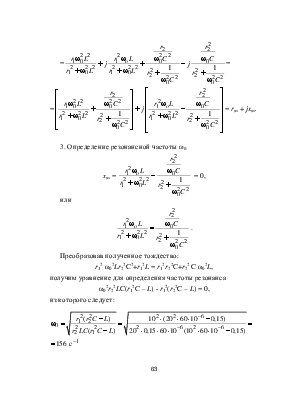
Задача 2

К цепи (рис. 2) приложено напряжение U = 10 В.

r₁ =10 Ом,    r₂  = 20 Ом,    L = 0,15 Гн,    C = 60 мкФ.

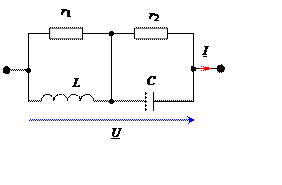Определить неразветв-ленный ток I и потреб-ляемую цепью мощность при резонансной частоте.

Решение

L

                1. Из условия  резонанса в цепи

Im(Z_вх) = Im(r_вх + jx_вх) = 0,

следует, что x_вх = 0.

	Рис. 2

 

2. Комплекс входного сопротивления цепи:

Z_вх =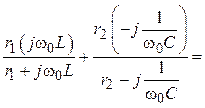

=

==

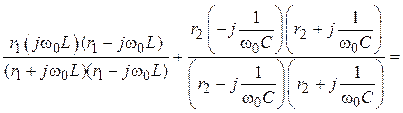
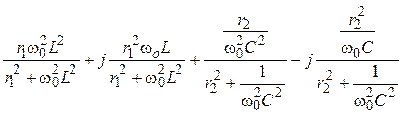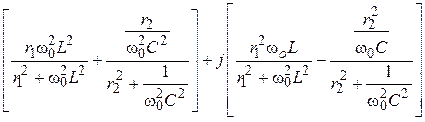== r_вх + jx_вх.

3. Определение резонансной частоты ω_0.

х_вх = 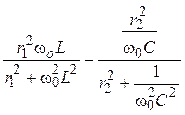 = 0,

или

.

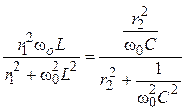Преобразовав полученное тождество:

r₁² ω₀²Lr₂²C²+r₁²L = r₁² r₂²C+r₂² C ω₀²L,

получим уравнение для определения частоты резонанса

ω₀²r₂²LC(r₁²C – L) - r₁²(r₂²C – L) = 0,

из которого следует:

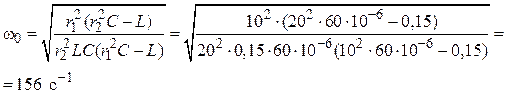
4. Определение входного тока:

=

=

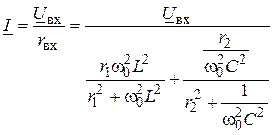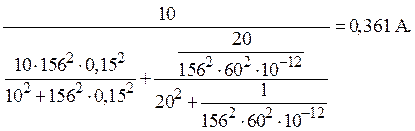
5. Определение активной мощности P₀:

P₀ = I² r_вх = 0,361²×27,7 = 3,61 Вт.

Ответ: I = 0,361 A, P₀ = 3,61 Вт.

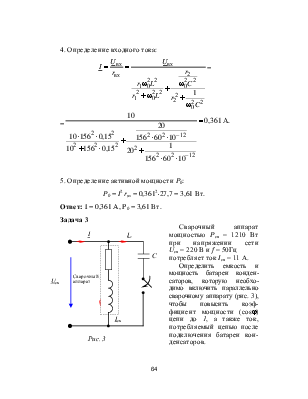
Задача 3                                         

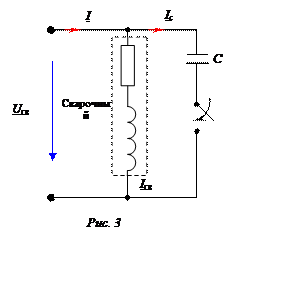Сварочный аппарат мощностью P_св = 1210 Вт при напряжении сети
U_св = 220 В и f = 50Гц

потребляет ток I_св = 11 А.

Сварочный аппарат

Определить емкость и мощность батареи конден-саторов, которую необхо-димо включить параллельно сварочному аппарату (рис. 3), чтобы повысить коэф-фициент мощности (соsj) цепи до 1, а также ток, потребляемый цепью после подключения батареи кон-денсаторов.

Решение

Вариант 1

1. Коэффициенту мощности, равному 1, соответствует режим резонанса токов в цепи (рис. 3), условием которого является:

Im(Y_вх) = Im(g_вх + jb_вх) = 0,

и, как следствие

b_вх = b_Lсв- b_C = 0.

2. Заданные характеристики сварочного аппарата (P_св, U_св, I_св) позволяют определить его коэффициент мощности

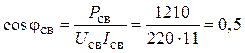
и реактивную проводимость

b_Lсв = Y_св sin j_н  = =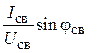

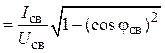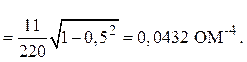Ом^-1.

3. Требуемая емкость определяется из условия резонанса

b_c =wС = b_Lсв = 0,0432 Ом^-1.

В результате

C =

4. Мощность батареи конденсаторов

Q_c =

5. Входной ток цепи может быть определен с помощью первого закона Кирхгофа

I = I_Lсв + I_c.

В режиме резонанса токов реактивная составляющая тока сварочного аппарата уравновешивается током батареи конденсаторов

= I_c,

поэтому входной ток цепи определяется лишь активной составляющей тока сварочного аппарата:

I =

Ответ:  С = 139 мкФ;  Q_C = 2100 Вар;  I = 5,5 A.

Вариант 2  (расчет с помощью векторной диаграммы).

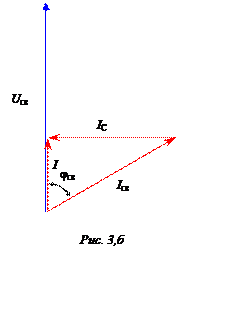Векторная диаграмма, соответствующая режиму резонанса (совпадения по фазе входного напряжения и входного тока), представлена на рис. 3,б. Диаграмма строится на основании первого закона Кирхгофа

.

Порядок построения диаграммы:

· в произвольном направлении строится вектор входного напряжения ;

· в соответствующем масштабе строится вектор тока сварочного агрегата , отстающий на угол

j_св = arccos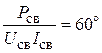

от вектора входного напряжения;

· к концу вектора пристраивается вектор емкостного тока , опережающий на прямой угол вектор входного напряжения, причем длина вектора емкостного тока принимается такой, чтобы вектор результирующего тока  оказался в фазе с вектором входного напряжения.

Диаграмма позволяет определить емкостный ток

I_C = I_свsinj_св = 11×sin 60° = 9,526 A,

и вслед за этим найти сопротивление конденсатора 

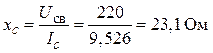
и величину емкости, обеспечивающей резонанс,

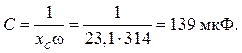
Задача 4

В цепи, изображенной на рис. 4,а, ток амперметра А равен 0.

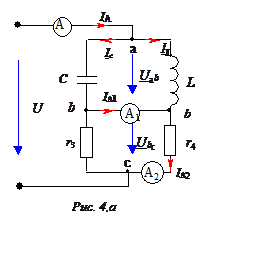     U = 240 B;

L = 40 мГн;

C = 1 мкФ.

Сопротивления амперметров равны 0.

Определить показания амперметров А₂ и А₁ (токи I_A1 и I_A2) .

Решение

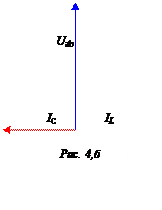
1. Так как I_А = 0, в цепи наблюдается резонанс токов на участке аb. Векторная диаграмма для этого случая показана на рис. 4,б.

Из условия резонанса

b_L0 – b_C0 = 0

следует, что частота резонанса

Рис. 4,а

ω₀ =

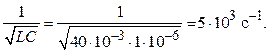
1. С учетом того что

,

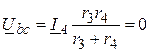из уравнения по второму закону Кирхгофа следует

U_ab = U – U_bc = U = 240 В.

В результате, ток в индуктивности

.

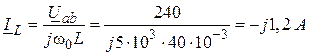3. Так как

I_A2  = ,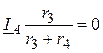

искомый ток через амперметр А₁, как сле-

дует из первого закона Кирхгофа для узла

«b»,

I_A1 = I_A2 – I₂ = 0 – (-j1, 2) = + j1,2  A.

Ответ:  I_A1 = 1,2 A.

Задачи для самостоятельного решения

Задача 5

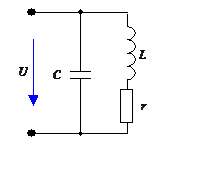Определить индуктивность L и входной ток цепи  в режиме резонанса, если

С = 58мкФ; U = 220 В; f = 50 Гц.

Расчет провести для случаев :

а) r =22 Ом,  б) r = 0.

Ответ:

а) L₁ = 0.139 Гн;  I_вх = 10 А

б) L₂ = 0.035 Гн,  I_вх = 0.

Задача 6

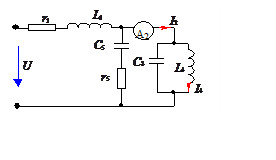Показание амперметра А₂ равно нулю. Чему равен ток I₄, если U = 200 B;  L₁ = 0,2 Гн;  r₁ = 50 Ом, C₃ = 10 мкФ; L₄ = 0,1 Гн; C₅ =5 мкФ;

r₅ = 50 Ом.

Построить векторную диаграмму токов и напряжений.

Рис. 6

Ответ: I₄ = 4,12 A.

Задача 7

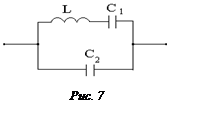Определить резонансные частоты в цепи, если L = 0,01 Гн;
С₁ = 0,25 мкФ; С₂ = 0,2 мкФ, активным сопротивлением цепи пренебречь.

Ответ: 1. Резонанс токов при

ω₁ = 3 ·10⁴ (1/с);

2. Резонанс напряжений при

ω₂ = 2 · 10⁴(1/c).

Задача 8

Определить индуктивность катушки L₂, если резонанс токов в цепи возникает при ω₀ = 2·10⁷ с^-1.

Параметры цепи:

r = 20 Ом;  L₁ = 20 мГн;  С = 6,25 мкФ.

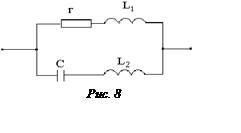Ответ: L₂ = 15 мГн.

Задача 9

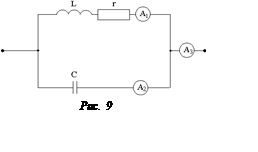
В цепи, изображенной на
рис. 9, имеет место резонанс токов. Амперметр А₁ показывает
6 А, показание амперметра А₃ составляет 3,6 А. Определить показание А₂.

Ответ:  I_А2 = 4,8 А.

Задача 10

Цепь находиться в состоянии резонанса Е = 40 В;

U_L = 30 B; U₁₂ = 50 B.

Мощность, потребляемая цепью, Р = 40 Вт.

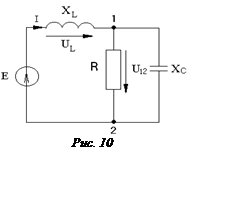Определить: R, x_L, x_C.

Ответ:  R = 12,5 Ом;  x_L = 6 Ом;  x_C = 16,6 Ом.