(Временные зависимости тока и напряжения по результатам расчета могут быть построены с помощью пакета Math Cad для каждой гармоники и для всей кривой в целом и снабжены необходимыми пояснениями.)
6. Результаты расчета занести в табл. 3.1
Т а б л и ц а 3.1
|
Номер |
ЭДС |
I1 |
I2 |
I3 |
Pпотр |
Pгенер |
|
1 |
||||||
|
2 |
||||||
|
3 |
||||||
|
Действующее |
PΣпотр |
PΣгенер |
||||
Указания к расчету
1. Как известно, любая периодическая функция может быть разложена в ряд Фурье:
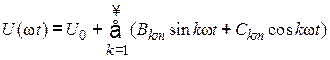 .
.
U0 и коэффициенты ![]() и
и![]() отыскиваются по следующим формулам:
отыскиваются по следующим формулам:
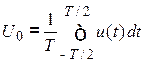 ;
;
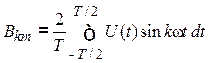 ;
;
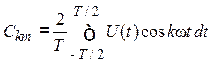 .
.
2. Расчет ведется методом наложения. При этом для каждой гармоники приложенного напряжения необходимо составить соответствующую электрическую схему и произвести расчет.
При расчете схемы для каждой гармоники необходимо пересчитать реактивные сопротивления. Следует обратить внимание на то, что индуктивные сопротивления возрастают пропорционально номеру гармоники, а емкостные сопротивления уменьшаются.
Для нулевой гармоники частота (ω(0) = 0):
![]() , т.е. индуктивности закорачиваются,
, т.е. индуктивности закорачиваются,
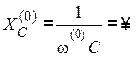 , т.е. конденсаторы представляют
разрыв.
, т.е. конденсаторы представляют
разрыв.
Сопротивления по первой гармонике:
![]() ,
, 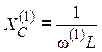 .
.
Сопротивления по k-й гармонике:
![]() ,
,
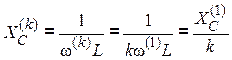 .
.
3. Записать мгновенное значение тока как сумму гармонических составляющих
![]() ,
,
где k – номер гармоники.
4. Потребляемая активная мощность
![]() ,
,
где Р1, Р2, Р3 – активные мощности первой, второй и третьей ветвей соответственно.
![]() .
.
Мощности Р2 и Р3 определяются аналогично.
5. Полная мощность цепи
![]() .
.
Пример расчета цепи
Рассмотрим один из вариантов электрической цепи, заданный в варианте 1 табл. 3.2. Тогда получим электрическую цепь рис. 3.2
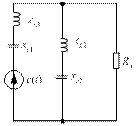
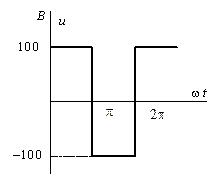
Рис. 3.2 Рис. 3.3
1. Разложим ЭДС, заданную на рис 3.3, в тригонометрический ряд Фурье. Заданная кривая ЭДС симметрична относительно оси абсцисс и раскладывается в ряд, который не содержит четных гармоник и постоянной составляющей. Таким образом,
![]() ,
,
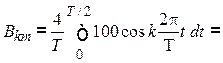
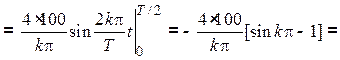
![]() .
.
Таким образом, ряд имеет вид
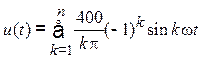 ,
,
где k = 1, 3, 5, …, или
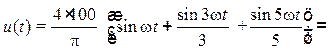
![]() .
.
Рассчитаем электрическую цепь, рис. 3.2, используя метод наложения, отдельно от каждой гармоники приложенного напряжения
Параметры цепи по первой гармонике:
![]() ,
,
![]() .
.
Входное сопротивление цепи относительно ЭДС:
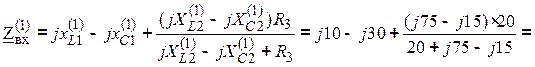
![]() ;
;
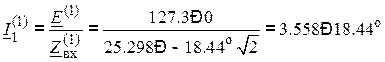 ;
;
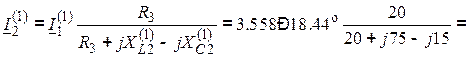
![]() ;
;
![]()
![]() .
.
Параметры цепи по третьей гармонике:
![]() Ом,
Ом, 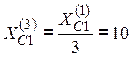 Ом,
Ом,
![]() Ом,
Ом,  Ом,
Ом,
![]() Ом.
Ом.
Входное сопротивление цепи по третьей гармонике:
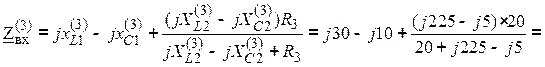
![]() Ом.
Ом.
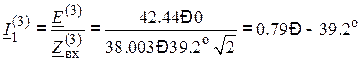 А,
А,
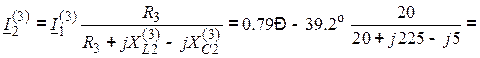
![]() А,
А,
![]()
![]() А.
А.
Параметры цепи по пятой гармонике:
![]() Ом,
Ом, 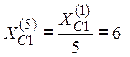 Ом,
Ом,
![]() Ом,
Ом, ![]() Ом.
Ом.
Входное сопротивление по пятой гармонике:
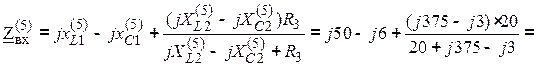
![]() Ом,
Ом,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.