Министерство высшего и среднего специального образования РСФСР
Сибирский ордена Трудового Красного Знамени металлургический институт имени Серго Орджоникидзе
ПРОВЕРКА ОСНОВНОГО УРАВНЕНИЯ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА МАЯТНИКЕ ОБЕРБЕКА
(Методические указания к выполнению лабораторной работы по курсу «Общая физика")
Издание СМИ Новокузнецк 1985
УДК 531.38 (075)
Рассмотрен метод проверки основного уравнения динамики вращательного движения твердого тела на основе исследования зависимости углового ускорения от момента инерции тела и момента приложенных сил.
Предназначены для студентов всех специальностей.
Рецензент - кафедра высшей математики Сибирского металлургического института (зав. кафедрой В.П. Белкин).
краткая теория
Основной закон динамики вращения: скорость изменения момента импульса тела равна результирующее моменту ом, действующих на тело:
![]() (1)
(1)
где ![]() - момент импульса;
- момент импульса;
Á - момент инерции;
`w - угловая скорость ;
`М - момент сил.
Если момент инерции тела при вращении во времени не меняется, то
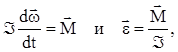 (2)
(2)
где ![]() - угловое ускорение.
- угловое ускорение.
При вращении около неподвижной оси момент сил и угловое ускорение направлено так, что о конца каждого из этих векторов вращение представляется происходящим против часовой стрелки.
Основное уравнение динамики вращательного движения тела утверждает, что угловое ускорение вращения тела прямо пропорционально моменту положенных сил и обратно пропорционально моменту инерции тела. Поэтому для проверки закона нужно:
- исследовать зависимость e = e(М) при Á =const;
- намерить момент инерции маятника;
- исследовать зависимость e = e(Á) при М = const.
Полученные зависимости представить в виде графиков.
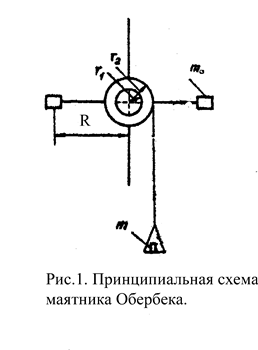 Маятник
(рис.1) состоит из четырех спиц, укрепленных на оси под прямым углом друг к другу.
На ту же ось насажены два шкива различных радиусов – r1
и r2. Вся система может вращаться вокруг
горизонтальной оси. Момент инерции прибора можно изменять, передвигая грузы m0 вдоль спиц или изменяя их число на спицах. На
шкив маятника навита нить. Привязанная к ней легкая платформа известной массы
служит для размещения грузов.
Маятник
(рис.1) состоит из четырех спиц, укрепленных на оси под прямым углом друг к другу.
На ту же ось насажены два шкива различных радиусов – r1
и r2. Вся система может вращаться вокруг
горизонтальной оси. Момент инерции прибора можно изменять, передвигая грузы m0 вдоль спиц или изменяя их число на спицах. На
шкив маятника навита нить. Привязанная к ней легкая платформа известной массы
служит для размещения грузов.
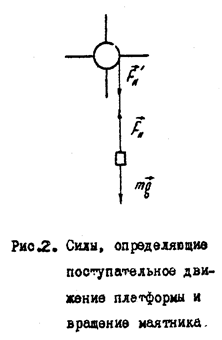
Вращающий момент создается силой натяжения нити FH’ (моментами сил трения и сопротивления пренебрегаем):
![]() (3)
(3)
где радиус шкива, r равен r1 или r2.
По третьему закону Ньютона ![]() .
.
Силу FH находим из уравнения движения платформы с грузом:
mg – FH = ma, (4)
где m - масса груза о платформой,
a - ускорение.
 Измеряя время ti, в течение которого нагруженная платформа из состояния покоя опускается
на расстояние hi,
можно показать, что при постоянной
массе платформы отношение 2hi/ti
не зависит от расстояния hi, т.е. ускорение движения платформы является
постоянной величиной. Тогда
Измеряя время ti, в течение которого нагруженная платформа из состояния покоя опускается
на расстояние hi,
можно показать, что при постоянной
массе платформы отношение 2hi/ti
не зависит от расстояния hi, т.е. ускорение движения платформы является
постоянной величиной. Тогда
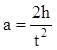 ,
(5)
,
(5)
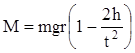 (6)
(6)
и
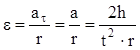 . (7)
. (7)
Последнее выражение учитывает нерастяжимость нити и отсутствие ее проскальзывания относительно шкива.
Из закона сохранения механической энергии при вращении маятника
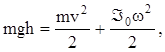 (8)
(8)
где mgh - потенциальная энергия платформы с грузом на высоте h от выбранного уровня отсчета;
![]() - кинетическая энергия
поступательного движения платформы с грузом на уровне отсчета;
- кинетическая энергия
поступательного движения платформы с грузом на уровне отсчета;
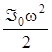 - кинетическая энергия
вращательного движения маятника в момент времени
- кинетическая энергия
вращательного движения маятника в момент времени 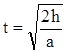 , в
который груз m достигает уровня отсчета.
, в
который груз m достигает уровня отсчета.
Из (8) можно найти момент инерции маятника Á0, измеряя время движения t.Так как
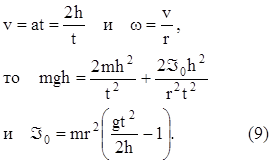
Считая грузы на спицах материальными точками и учитывая, что момент инерции твердого тела является величиной аддитивной, можем найти момент инерции маятника:
![]() (10)
(10)
где Ri - расстояние от грузов m0 до оси маятника.
Приборы и принадлежности: маятник Обербека, набор грузов, секундомер, линейка.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Проверка зависимости e = e(М):
1.1. Поднять площадку на высоту h относительно выбранного уровня отсчета, намотав нить на шкив радиусом r1/
1.2. Поместить груз массы m на площадку и измерить время его движения до выбранного уровня отсчета (измерения повторить не менее 5-6 раз ).
1.3. Выполнить измерения согласно пункту 1.2 для пяти различных грузов на площадке. Результаты занести в таблицу по нижеприведенной форме.
Результаты измерений
|
mi |
r1 |
|||||
|
t1 |
t2 |
t3 |
t4 |
t5 |
tср |
|
1.4. Аналогичные измерения провести для шкива радиусом r2. Результаты занести в таблицу (форму таблицы смотрите ниже).
Результаты измерений
|
mi |
r1 |
|||||
|
t1 |
t2 |
t3 |
t4 |
t5 |
tср |
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.