Экспериментальное изучение свойств физического маятника (Лабораторная работа № 16к)

Лабораторная работа №16к.

ЭКСПЕРИМЕНТАЛЬНОЕ ИЗУЧЕНИЕ СВОЙСТВ

ФИЗИЧЕСКОГО  МАЯТНИКА.

Теория физического маятника.

Определения.

Физическим маятником  называется твёрдое тело произвольной формы, имеющее возможность совершать колебательное движение вокруг неподвижной оси  (рис.1).

Центром тяжести (центром массы) твёрдого тела называется точка, относительно которой твёрдое тело находится в состоянии безразличного равновесия в однородном поле тяжести. Поэтому радиус-вектор, определяющий положение центра масс в пространстве, вычисляется по формуле:

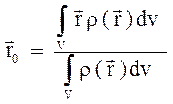.                                                             (1)

Моментом инерции твёрдого тела относительно заданной оси называется скалярная величина, характеризующая инерционные свойства тела во вращательном движении, и определяется распределением массы около этой оси:

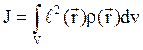,         (2)

где - расстояние от точки с радиусом  до выделенной оси; плотность тела в заданной точке ; V-объём.

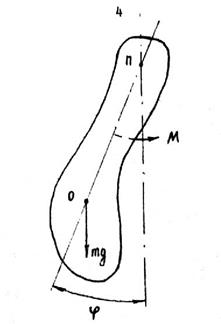
Рис.1. Физический маятник (схема).

Рис.2. К теореме Штейнера: -ось, проходящая через центр масс; nn' - произвольная ось.

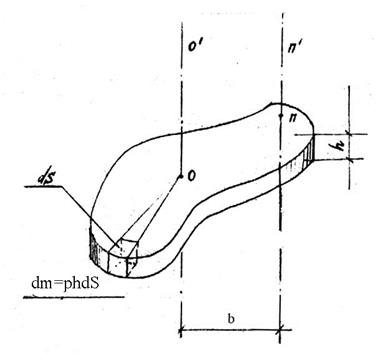Момент инерции является аддитивной величиной и может быть найден по теореме Штейнера (рис. 2).

,                                                                                 (3)

где Á-момент инерции относительно nn'

      Á_о- момент инерции относительно центральной оси  (центральный момент инерции);

      m-масса тела;

      b-расстояние между осями.

Период между колебаний физического маятника.

Влияние трения на величину периода.

В соответствии с основным законом динамики вращательного движения  

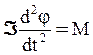                                                                                          (4)

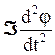где Á – момент инерции маятника относительно оси колебаний;

-  угловое ускорение маятника;

-   

М=М_тяг.+М_тр. – суммарный момент сил, действующих на маятник, относительно оси колебаний;

 - момент  сил тяжести;

m – масса тела;

g – величина ускорения свободного падения;

 - расстояние от центра тяжести (масс) тела до оси колебаний;

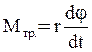 - момент сил вязкого трения;

r – коэффициент трения;

 - угловая скорость маятника.

Введя обозначения 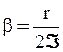 и 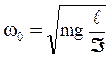, запишем уравнение

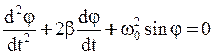                                                         (4а)

Для , рад., поэтому

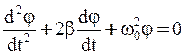                                                                (5)

где  - коэффициент затухания;

- частоты затухающих и собственных колебаний.

Период 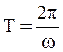, Поэтому

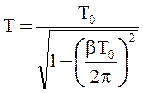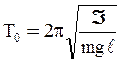;  .                                  (7)

По определению логарифмического декремента затухания находим его связь с и Т₀ в форме

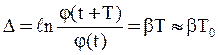                                                            (8)

или в форме

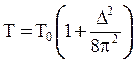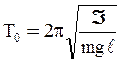; .                                                (9)

Зависимость периода колебаний от амплитуды.

В предыдущем разделе показано, что при период колебаний маятника практически не зависит от амплитуды. Рассмотрим решение для произвольного . Без учёта трения на основании закона сохранения механической энергии имеем:

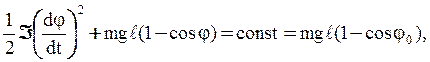  (10)

где 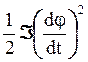-киническая энергия маятника;

 - потенциальная энергия;

 - полная механическая энергия;

- амплитуда угла отклонения.

Решая уравнение (10), получаем выражение для периода колебаний:

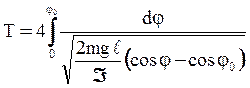,                                         (11)

или приближённо

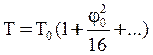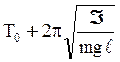; .                                  (12)

Влияние амплитуды на период при углах  незначительно. (При , например, относительное увеличение периода составляет 1 %).

Зависимость периода колебаний от массы маятника.

В формулах (9) и (12) отношение  и Т₀ от массы маятника не зависят. Независимость периода колебаний от амплитуды является следствием свойств сил тяготения. Однако силы трения имеют другую природу. Из определения логарифмического декремента следует:

.

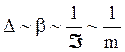Поэтому, если увеличить массу маятника, сохраняя при этом его геометрические размеры, влияние сил трения может быть уменьшено. Соответственно (9) небольшому уменьшению подвергается и период колебаний физического маятника.

Влияние положения оси колебаний маятника на величину

 периода колебаний маятника.

Количественная зависимость  представлена формулами (9) и (12). Учитывая, что , имеем:

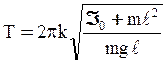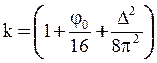;  .                                  (14)

Для анализа удобно пользоваться величиной  (центральная длина физического маятника), определяемой по формуле