Теплофизические параметры весьма различающихся твердых тел определяют как с помощью стандартизованного оборудования, выпускаемого серийно - дериватографов, дилатометров, калориметров, так и с использованием уникальных установок и устройств, специально создаваемых для исследования конкретного объекта. Такие устройства обладают всегда рядом индивидуальных особенностей, вместе с тем, установки и методики, созданные разными авторами, но предназначенные для измерения однородных величин, имеют и много общего. Общим признаком многих современных измерительных устройств является использование микропроцессоров и ЭВМ для проведения измерений в строго контролируемых условиях и облегчения математической обработки результатов. По сути дела, новейшие экспериментальные установки - это измерительно-вычислительные комплексы.
Ввиду большого разнообразия методик измерения укажем лишь некоторые, принципиально важнейшие в последовательности рассмотрения материала ч.1, 2.
Поверхность
Ферми есть поверхность постоянной энергии ЕF в пространстве волновых
векторов (![]() -пространстве). Поверхность Ферми при абсолютном
нуле отделяет заполненные электронами состояния от свободных. В простейшем
случае свободного электрона поверхность Ферми представляет собой сферу радиусом
kF (рис.3.10.1), причем между kF и ЕF существует простая аналитическая
связь:
-пространстве). Поверхность Ферми при абсолютном
нуле отделяет заполненные электронами состояния от свободных. В простейшем
случае свободного электрона поверхность Ферми представляет собой сферу радиусом
kF (рис.3.10.1), причем между kF и ЕF существует простая аналитическая
связь:
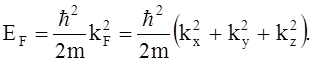 (3.10.1)
(3.10.1)
В
кристаллической решетке на значения k
накладываются периодические граничные условия, в случае кубической решетки с периодом
“a” волновой вектор ![]() характеризуется набором значений:
характеризуется набором значений:
kx, ky,
kz = 0; 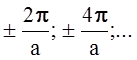
В результате в энергетическом спектре появляются
щели запрещенных значений, не все значения волнового вектора ![]() становятся равновероятными. Форма
поверхности Ферми отклоняется от сферической тем больше, чем сложнее решетка, и
вообще может быть весьма сложной. Построение облегчается учетом свойств зон
Бриллюэна (ячеек решетки в
становятся равновероятными. Форма
поверхности Ферми отклоняется от сферической тем больше, чем сложнее решетка, и
вообще может быть весьма сложной. Построение облегчается учетом свойств зон
Бриллюэна (ячеек решетки в ![]() - пространстве).
- пространстве).
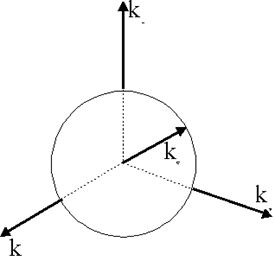 Рис.3.10.1.Поверхность Ферми системы из N
свободных электронов, находящихся в основном состоянии
Рис.3.10.1.Поверхность Ферми системы из N
свободных электронов, находящихся в основном состоянии
Поверхности Ферми в значительной мере важны лишь при описании поведения металлов в электрических и магнитных полях, но подробно они здесь рассматриваться не будут. Укажем лишь, что построению поверхностей Ферми посвящено очень много теоретических и экспериментальных исследований. Принцип построения достаточно прост и подробно изложен, например, в монографии Д.Анималу.
Для экспериментального изучения поверхности Ферми (а, следовательно, и значений энергии Ферми) в металлах разработан ряд мощных методов, которые используют:
а) отражение света от поверхности металла;
б) циклотронный резонанс;
в) аномальный скин-эффект (распространение высокочастотных токов в поверхностном слое металла);
г) распространение ультразвуковой волны в условиях наличия магнитного поля;
д) эффект магнетосопротивления структуры;
е) эффект де Гааза - ван Альфена, заключающийся в том, что магнитные момент металлического образца в сильном магнитном поле и при низких температурах становится периодической функцией магнитного поля.
Обзор теории методов (пп. б,г) и основные результаты изложены в известной книге Ч.Киттеля "Введение в физику твердого тела".
Фонон
характеризуется волновым вектором ![]() и взаимодействует с
другими частицами, квазичастицами и полями так, что его взаимодействие можно
описывать, используя квазиимпульс
и взаимодействует с
другими частицами, квазичастицами и полями так, что его взаимодействие можно
описывать, используя квазиимпульс ![]()
 Фононный спектр тела может быть исследован с
использованием эффектов неупругого взаимодействия фононов с фотонами и нейтронами.
Пусть с пучком фононов (звуковой волной) в кристалле взаимодействует фотон.
Показано экспериментально, что интенсивный лазерный пучок фотонов рассеивается
решеткой и при этом наблюдается смещение частоты фотонов, объясняемое рождением
фононов в процессе взаимодействия с решеткой световой волны.
Фононный спектр тела может быть исследован с
использованием эффектов неупругого взаимодействия фононов с фотонами и нейтронами.
Пусть с пучком фононов (звуковой волной) в кристалле взаимодействует фотон.
Показано экспериментально, что интенсивный лазерный пучок фотонов рассеивается
решеткой и при этом наблюдается смещение частоты фотонов, объясняемое рождением
фононов в процессе взаимодействия с решеткой световой волны.
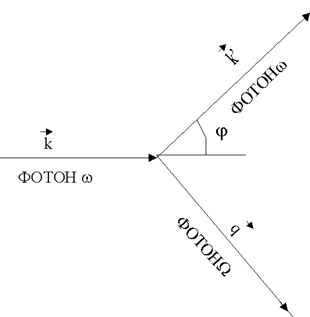
Рис.3.10.2.Схема неупругого рассеяния решеткой фотона с волновым вектором k
Схематически
этот процесс можно представить в виде диаграммы (рис.3.10.2). В результате
взаимодействия образуется фонон с волновым вектором ![]() , а
волновой вектор фотона изменяется от
, а
волновой вектор фотона изменяется от ![]() до
до ![]() .
.
При количественном описании этого процесса можно использовать закон сохранения энергии и правило отбора для волнового вектора. По закону сохранения энергии
![]() (3.10.2)
(3.10.2)
а из выполнимости правила отбора следует, что
![]() (3.10.3)
(3.10.3)
где для простоты не учитывается возможность брэгговской дифракции.
Схему
расчета можно упростить, если учесть, что, из-за большой разности в скоростях
света и звука, фонону может быть передана лишь малая часть энергии фотона, т.е.
не будет сделано большой ошибки, если предположить ![]() .
Действительно, для фонона W = Vq, где V - скорость звука в твердом теле, но тогда,
при сравнимых значениях величин `k и `q, волновых векторов фотона и фонона,
частота фотона w = ck много выше W, т.е. w>>W,
так как c>>V. Это позволяет трансформировать диаграмму
рис.3.10.2 к виду рис.3.10.3, где треугольник волновых векторов является
равнобедренным.
.
Действительно, для фонона W = Vq, где V - скорость звука в твердом теле, но тогда,
при сравнимых значениях величин `k и `q, волновых векторов фотона и фонона,
частота фотона w = ck много выше W, т.е. w>>W,
так как c>>V. Это позволяет трансформировать диаграмму
рис.3.10.2 к виду рис.3.10.3, где треугольник волновых векторов является
равнобедренным.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.