действующей силы, `e - угловое ускорение, J - момент инерции вращающегося тела.
Для его проверки надо убедиться,
что грузики на первом участке движутся равноускоренно (скорость описывается формулой V = at, а высота падения 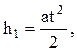 отreда V2 = 2ah1).
отreда V2 = 2ah1).
Рассматриваем зависимость V2 = ah1, и определяем a из метода наименьших квадратов.
2.1. Проверка равноускоренного движения грузиков.
Установите верхний кронштейн на высоте, заданной преподавателем. Измерьте время падения и результат занесите в табл.1.2.
(Замеры проведите для трех разных высот).
|
№ оп. |
hi |
ti |
Vi |
Vi2 |
Vi2×hi |
hi2 |
a×hi |
Vi2-a×hi |
(Vi2-a×hi)2 |
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
1 |
|||||||||
|
2 |
|||||||||
|
3 |
|||||||||
|
|
|||||||||
Постройте график V2(h) = a×h и убедитесь, что экспериментальные
точки лежат вблизи прямой. Это доказывает, что грузики на первом участке движутся равноускоренно, т.e. ![]() . Поскольку a = e×r , шкив также вращается равноускоренно
(e = const).
. Поскольку a = e×r , шкив также вращается равноускоренно
(e = const).
2.2. Проверка адекватности результатов, полученных из расчетов и экспериментов (п. 2.2. выполняется по отдельному указанию преподавателя для всех студентов, для студентов, обучающихся по программе магистров – обязателен).
Проведите расчеты для столбцов 4-7 и определите величину a
по расчетной формуле из метода наименьших квадратов:
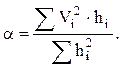
Зная a, заполните столбцы 8-10 и определите дисперсию адекватности
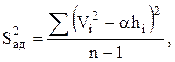 где n – число опытов.
где n – число опытов.
Сопоставьте дисперсию адекватности Sад2 с дисперсией опыта по F – критерию: 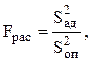 если
если ![]() движение
можно считать равноускоренным. (Подробнее см., например: Н.Джонсон, Ф.Лион
«Статистика и планирование эксперимента в технике и науке. Методы обработки
данных»,т.1,2 -М., «Мир», 1980 г.).
движение
можно считать равноускоренным. (Подробнее см., например: Н.Джонсон, Ф.Лион
«Статистика и планирование эксперимента в технике и науке. Методы обработки
данных»,т.1,2 -М., «Мир», 1980 г.).
2.3. Проверка неизменности соотношения M/e и определение момента инерции кольца.
Наложить на диск-держатель стальное кольцо.
Установите верхний кронштейн на указанной преподавателем высоте и проведите замеры времени равномерного движения системы для трех различных перегрузков. Результаты внесите в табл. 1.3.
Таблица 1.3
|
№оп |
mп i |
ti |
Vi |
Vi2 |
ai |
ei |
Mi |
Mi/ei=Ji |
DJi |
DJi2 |
|
1 |
||||||||||
|
2 |
||||||||||
|
3 |
||||||||||
|
|
||||||||||
|
JСР = |
Sад2= |
|||||||||
Проведите расчеты и заполните табл.1.3 .
Расчетные формулы:
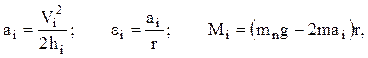
где mn, m, r - масса перегрузки, масса грузиков и радиус шкива соответственно.
Если М/e = const, уравнение вращательного движения имеет вид M=J×e, т.е. величина M/e соответствует сумме моментов инерции кольца и диска-держателя, обозначаемого в дальнейшем Jд.
Величину Jд определите по значению a из упражнения 2. Рассчитайте величину момента инерции кольца JK из выражения
JK = Jср - Jд.
Оцените погрешность определения JK.
Проконтролируйте результаты измерения JK, проведя расчет его по теоретической формуле
![]()
где mк - масса кольца.
Данные для расчетов:
m = 60 г, r = 40 мм, Dвнеш =106 мм, Dвнут = 86 мм.
Массы перегрузков mn и кольца указаны на их поверхности.
1. Дайте определение величин момента силы `М, углового ускорения `e и момента инерции J.
2. Выведите расчетные формулы для `М и `e м уравнений динамики.
3. Выведите формулу для момента инерции кольца JK, как момента инерции тела с распределенной массой.
4. Укажите, какова аналитическая связь между линейными и угловыми характеристиками движения: `а; `e; `V; `w.
5. Определите направление
векторов ![]() при различных направлениях
равномерного, равноускоренного, равнозамедленного вращения тела.
при различных направлениях
равномерного, равноускоренного, равнозамедленного вращения тела.
ЛАБОРАТОРНАЯ РАБОТА №1-4
ИЗУЧЕНИЕ МОМЕНТА ИНЕРЦИИ ТВЕРДЫХ ТЕЛ
Цель работы, ознакомление с методом измерения момента инерции; экспериментальная проверка свойств момента инерции.
Приборы и принадлежности, крутильный маятник ГРМ-05; набор исследуемых тел.
Со школьных времен привычным является определение, "мерой инерции тел является масса" и не всегда помнится, что это определение справедливо лишь при поступательном движении тела или при движении материальной точки. Если тело совершает вращательное движение, его инертность определяется не только массой, но и распределением массы относительно оси вращения. Рассматривая твердое тело как идеально твердое, как недеформируемую совокупность N материальных точек массой mi, с помощью второго закона Ньютона можно получить следующее соотношение, справедливое в случае вращения тела относительно закрепленной оси А:
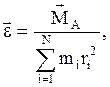 (4.1)
(4.1)
где ![]() - полный
момент сил, действующих на тело относительно оси А;
- полный
момент сил, действующих на тело относительно оси А; ![]() - угловое ускорение тела; ri
-
расстояние от i-той материальной
точки до оси вращения.
- угловое ускорение тела; ri
-
расстояние от i-той материальной
точки до оси вращения.
Соотношение (4.1), описывающее динамику вращательного движения, по своей структуре аналогично второму закону Ньютона,
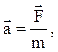 (4.2)
(4.2)
описывающему динамику движения материальной точки. Сравнение соотношений (4.1) и (4.2) позволяет сделать вывод о том, что роль момента инертности при вращательном движении играет величина
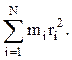 Эта
величина называется моментом инерции твердого тела относительно заданной
оси вращения (А):
Эта
величина называется моментом инерции твердого тела относительно заданной
оси вращения (А):
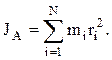
Поскольку существует бесконечное множество осей вращения тела, может показаться, что невозможно задать инертные вращательные свойства твердого тела некоторой единой физической величиной, играющей ту же роль, что и масса при поступательном движении
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.