межатомное расстояние (длина ребра элементарной кубической ячейки ) или период решетки.
Для системы плоскостей, параллельных какой-либо грани кубической решетки, dhkl совпадает с а.
При прохождении монохроматического пучка электронов сквозь поликристаллическую пленку, вследствие хаотичности в, ориентации монокристалликов в пленке, всегда найдутся системы кристаллических плоскостей, расположенных по отношению к падающему пучку под углами, удовлетворяющими условию (4). Электронные пучки, рассеянные под углом q, образуют коническую поверхность с осью, направленной вдоль падающего пучка, и углом при вершине, равным 2 q (рис. 2). На экране Э, установлением на пути электронов, рассеянных от каждой системы плоскостей, возникает дифракционное кольцо радиуса г. Поэтому полученная электронограмма представляет собой систему концентрических колец, как, например, электронограмма меди (рис.2,б).
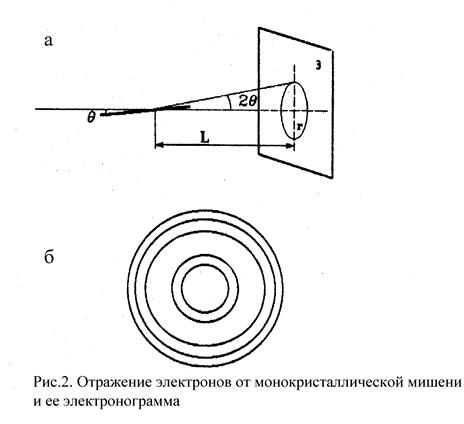
Как видно из рис. 1.2, а, радиус кольца связан с углом в соотношением
![]()
где L - расстояние от поликристаллической пленки до экрана. При малых углах
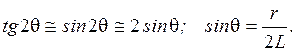 (6)
(6)
Из уравнений (4) и (6) находим
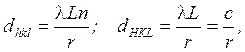 (7)
(7)
где dHKL - межплоскостное расстояние, равное dhkl, деленному на порядок отражения n; с - постоянная прибора.
Использовав соотношение (5), получим
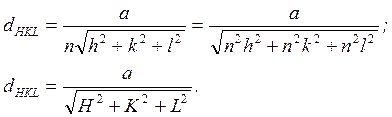 (8)
(8)
Здесь НКL - индексы интерференции. Они определяются произведением индексов семейства плоскостей hkl на порядок отражения n:
Н = nh, К = nk, L = nl.
Так как числа, образующие индексы h, k, 1, не могут иметь общего делителя, то, зная индексы интерференции НКL данного кольца, можно определить порядок интерференционного максимума и индексы плоскостей, при отражении от которых получалось данное кольцо. Например, кольцо с индексами HKL, равными 200, получилось в результате отражения второго порядка от плоскостей 100, а кольцо 400 - благодаря отражению четвертого порядка от тех же плоскостей. Кольцо 420 - результат отражения второго порядка .от плоскостей 210 и т.д.
Из формулы (8) видно, что каждому значению d соответствуют определенные значения индексов интерференции НKL, определение которых производится методом проб разными способами для разных сингоний; исходной формулой во всех случаях является соотношение Вульфа-Брегга. Возможные индексы интерференции для первых шести колец электронограммы решеток кубической сингонии приведены в табл. 1.
Определение типа кристаллической решетки вещества по его электронограмме даже с применением ЭВМ представляет сложную задачу. В данной лабораторной работе задача облегчена тем, что выдаются электронограммы с указанным заранее типом сингонии - кубической. И даже в этом случае возможны затруднения вследствие того, что в предложенных электронограммах может недоставать некоторых колец или есть кольца вторичных дифракционных максимумов.
Таблица 1
|
Номер дифракци- онного кольца |
Решетка кубическая |
|||||
|
объемно-центрированная (ОЦК) |
гранецентрированная (ГЦК) |
типа алмаза |
||||
|
HKL |
H2+K2+L2 |
HKL |
H2+K2+L2 |
HKL |
H2+K2+L2 |
|
|
1 |
110 |
2 |
111 |
3 |
111 |
3 |
|
2 |
200 |
4 |
200 |
4 |
220 |
8 |
|
3 |
211 |
6 |
220 |
8 |
311 |
11 |
|
4 |
220 |
8 |
311 |
11 |
400 |
16 |
|
5 |
310 |
10 |
222 |
12 |
331 |
19 |
|
6 |
222 |
12 |
400 |
16 |
422 |
24 |
Расчет электронограмм поликристаллических образцов сводится к определению межплоскостных расстояний по формуле (7). Для расчета удобно находить отношение Q квадрата межплоскостного расстояния первого кольца к квадрату межплоскостного расстояния каждого последующего кольца:
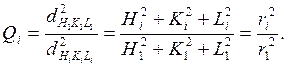
Расчет Q производится именно по отношению квадрата радиуса i-го кольца (i = 1,2,3,4,5,6) к квадрату радиуса первого кольца:
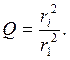 (9)
(9)
Значения отношений Q для первых шести колец электронограммы кубических решеток приведены в табл.2.
Для расшифровки электронограммы нужно найти ряд отношений Qi и на основании табл.2 определить тип кристаллической решетки вещества. Полученные значения Q могут не совпадать точно с табличною значениями, нужно находить в таком случае наиболее близкий ряд.
Таблица 1.2
|
Номер дифракционного кольца |
Р е ш е т к а к у б и ч е с к а я |
||
|
Объемно-центрированная (ОЦК) |
Гранецентрированная (ГЦК) |
Типа алмаза |
|
|
1 |
1 |
1 |
1 |
|
2 |
2 |
1,33 |
2,66 |
|
3 |
3 |
2.66 |
3,67 |
|
4 |
4 |
3,67 |
5,33 |
|
5 |
5 |
4 |
6,33 |
|
6 |
6 |
5,33 |
8 |
ПРИМЕЧАНИЕ. Более подробные таблицы можно найти в [1,стр.404-405].
Период кубической решетки рассчитывается по формуле
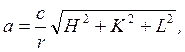 (10)
(10)
где с - постоянная электронографа, значение с указано на выдаваемой электронограмме; г - радиус i-го кольца; H2+K2+L2 - сумма квадратов индексов интерференции, соответствующих i-му кольцу (см. табл. 1).
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Получите фотографию электронограммы. Запишите вещество, которое она характеризует, и коэффициент с.
2. Измерьте радиусы г колец по порядку. Цена деления шкалы линейки 1 мм. Если кольца на электронограмме размыты, отсчет производите посередине полосы. Данные запишите в табл.3.
3. Вычислите значение Qi, где i = 1,2,3... - номера колец по порядку, гi2 - квадраты их радиусов, г12 - квадрат радиуса первого
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.